Cho tam giác ABC đều, có diện tích bằng \({s_1}\) và \(AH\) là đường cao. Quay tam giác ABC quanh đường thẳng \(AH\) ta thu được hình nón có diện tích xung quanh bằng \({s_2}\). Tính \(\dfrac{{{s_1}}}{{{s_2}}}\).
Giả sử tam giác ABC đều cạnh a \( \Rightarrow {s_1} = {S_{ABC}} = \dfrac{{{a^2}\sqrt 3 }}{4}\)
Quay tam giác ABC quanh đường thẳng \(AH\) ta thu được hình nón có đường sinh \(l = AB = a\), bán kính đáy \(r = \dfrac{{BC}}{2} = \dfrac{a}{2}\), do đó diện tích xung quanh của hình nón bằng: \({s_2} = \pi rl = \pi .\dfrac{a}{2}.a = \dfrac{{\pi {a^2}}}{2}\).
Vậy \(\dfrac{{{s_1}}}{{{s_2}}} = \dfrac{{\dfrac{{{a^2}\sqrt 3 }}{4}}}{{\dfrac{{\pi {a^2}}}{2}}} = \dfrac{{\sqrt 3 }}{{2\pi }}\).
Cho hình nón đỉnh \(S\) có bán kính đáy \(R = 2\). Biết diện tích xung quanh của hình nón là \(2\sqrt 5 \pi \). Tính thể tích khối nón.
Ta có : \({S_{xq}} = \pi Rl \Rightarrow 2\sqrt 5 \pi = \pi .2l \Leftrightarrow l = \sqrt 5 \).
Lại có \({l^2} = {R^2} + {h^2} \Leftrightarrow {\left( {\sqrt 5 } \right)^2} = {2^2} + {h^2}\)\( \Leftrightarrow {h^2} = 1 \Leftrightarrow h = 1\).
Vậy thể tích khối nón là : \(V = \dfrac{1}{3}\pi {R^2}h = \dfrac{1}{3}\pi {.2^2}.1 = \dfrac{4}{3}\pi \).
Cho hình nón tròn xoay có chiều cao \(h = 20(\;{\rm{cm}})\), bán kính đáy \(r\). Một thiết diện đi qua đỉnh của hình nón có chu vi là \(40 + 10\sqrt {41} (\;{\rm{cm}})\) và khoảng cách từ tâm đáy đến mặt phẳng chứa thiết diện là \(12(\;{\rm{cm}})\). Tính thể tích của khối nón.
\(V = \dfrac{{12500\pi }}{3}\left( {\;{\rm{c}}{{\rm{m}}^3}} \right)\)
\(V = \dfrac{{12500\pi }}{3}\left( {\;{\rm{c}}{{\rm{m}}^3}} \right)\)
\(V = \dfrac{{12500\pi }}{3}\left( {\;{\rm{c}}{{\rm{m}}^3}} \right)\)
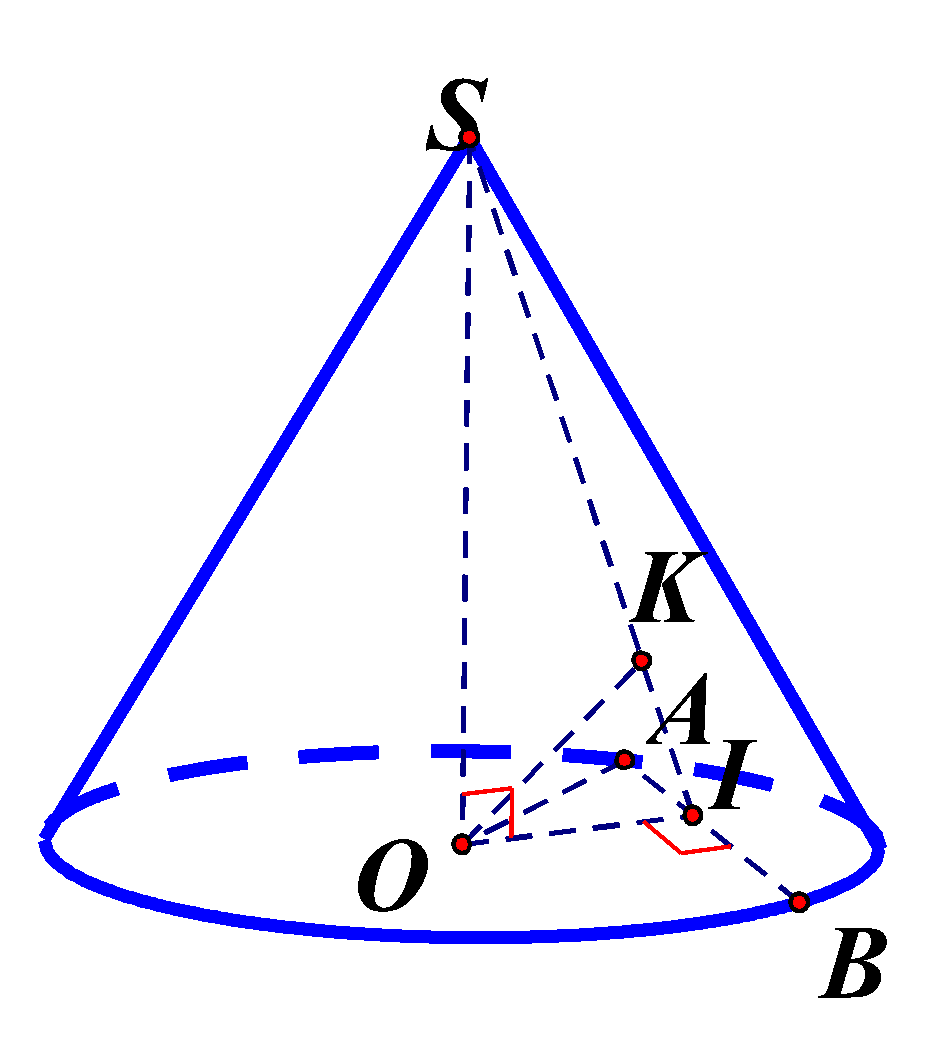
Bước 1: Tính SO, OI, AB và SA
Ta có \(SO = h = 20;OK = 12\).
Áp dụng hệ thức lượng cho tam giác vuông SOI có
\(\dfrac{1}{{O{K^2}}} = \dfrac{1}{{O{I^2}}} + \dfrac{1}{{O{S^2}}} \Rightarrow OI = 15(\;{\rm{cm}})\)
\(AB = 2AI = 2\sqrt {{r^2} - {{15}^2}} (\;{\rm{cm}})\)
\(SA = \sqrt {S{O^2} + O{A^2}} = \sqrt {{r^2} + {{20}^2}} (\;{\rm{cm}}).\)
Bước 2: Tính r và thể tích khối nón.
Mà chu vi thiết diện là \(40 + 10\sqrt {41} (\;{\rm{cm}})\) nên ta có:
\(AB + SA + SB = 40 + 10\sqrt {41} \)
\( \Leftrightarrow 2\sqrt {{r^2} - 225} + 2\sqrt {{r^2} + 400} \)\( = 40 + 10\sqrt {41} \)
\( \Leftrightarrow r = 25(\;{\rm{cm}})\)
\(AB + SA + SB - 40 + 10\sqrt {41} \)\( \Leftrightarrow 2\sqrt {{r^2}} - 225 + 2\sqrt {{r^2}} + 400\)\( = 40 + 10\sqrt {41} \)
Vậy thể tích khối nón là:
\({V_n} = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}\pi \cdot {25^2} \cdot 20\)\( = \dfrac{{12500\pi }}{3}\left( {\;{\rm{c}}{{\rm{m}}^3}} \right)\)
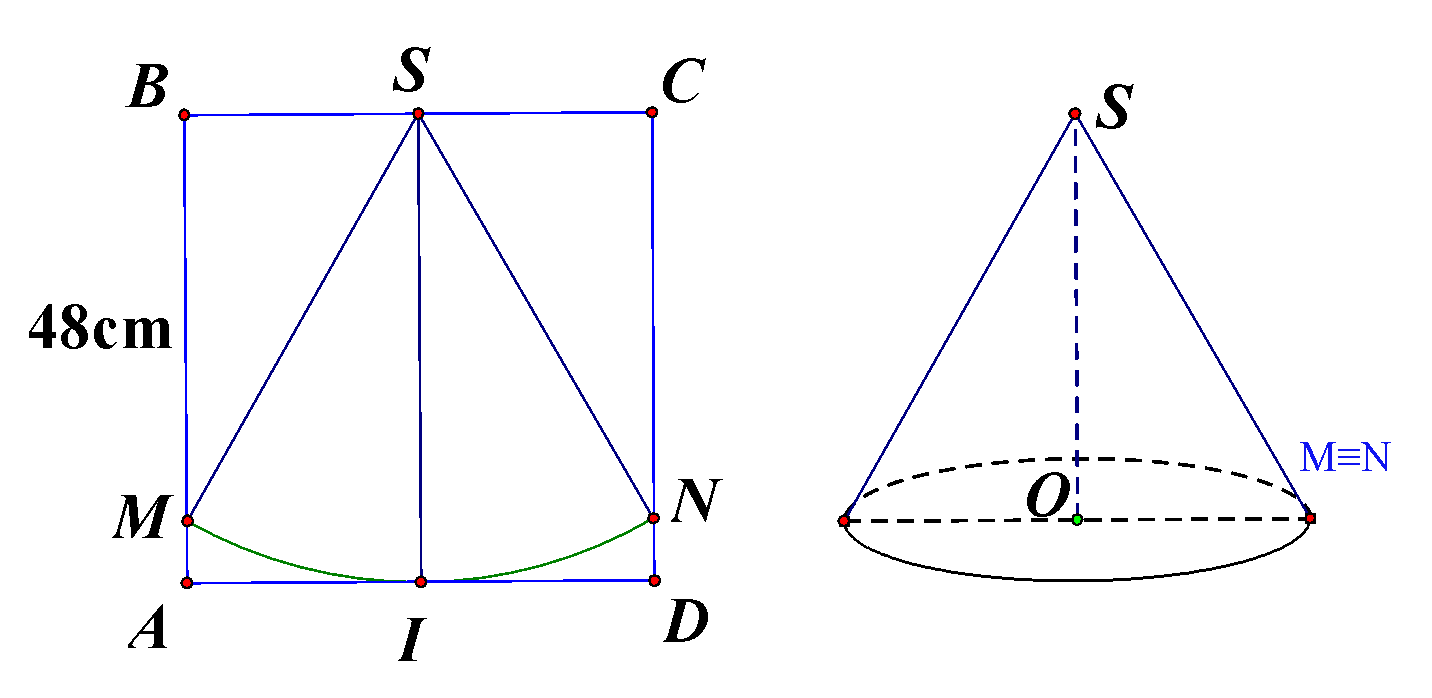
Cho một tấm bìa hình vuông ABCD có cạnh \(48\;{\rm{cm}}\). Gọi S, I lần lượt là trung điểm của BC và AD. Dùng compa vạch cung tròn MN có tâm là \(S\) và bán kính SI (hình vẽ) rồi cắt tấm bìa theo cung tròn đó. Dán phần hình quạt sao cho SM và SN trùng nhau thành một cái mũ hình nón không đáy với đỉnh \(S\) (giả sử phần mép dán không đáng kể). Tính thể tích \(V\) của cái mũ đó.
\(V = \dfrac{{512\pi \sqrt {35} }}{3}\left( {\;{\rm{c}}{{\rm{m}}^3}} \right)\).
\(V = \dfrac{{512\pi \sqrt {35} }}{3}\left( {\;{\rm{c}}{{\rm{m}}^3}} \right)\).
\(V = \dfrac{{512\pi \sqrt {35} }}{3}\left( {\;{\rm{c}}{{\rm{m}}^3}} \right)\).
Bước 1: Tính chiều dài dây cung MN
Ta có \(MN = SM = SN = 48\;{\rm{cm}}\) nên \(\Delta SMN\) đều
\( \Rightarrow \widehat {MSN} = {60^0}\).
Chu vi đường tròn đáy của cái mũ chính là chiều dài \(x\) của dây cung MN.
Bước 2: Tính chiều cao của cái mũ
Mặt khác số đo cung MN bằng số đo \(\widehat {MSN} = {60^0}\) nên \(x = \dfrac{{\pi .48.60}}{{180}} = 16\pi \).
Gọi \(r\) là bán kính của đường tròn đáy của cái mũ, ta có \(x = 2\pi r \Rightarrow r = \dfrac{x}{{2\pi }} = \dfrac{{16\pi }}{{2\pi }} = 8\).
Bước 3: Tính thể tích
Chiều cao của cái mũ \(h = \sqrt {S{M^2} - {r^2}} = \sqrt {{{48}^2} - {8^2}} = 8\sqrt {35} \).
Vậy thể tích cái mũ \(V = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}\pi {8^2}.8\sqrt {35} = \dfrac{{512\pi \sqrt {35} }}{3}\left( {\;{\rm{c}}{{\rm{m}}^3}} \right)\).
Cho hình hộp \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\) có đáy là hình thoi cạnh \(a\) và góc \(\widehat {BAD} = q\). Mặt chéo \(AC{C^\prime }{A^\prime }\) nằm trong mặt phẳng vuông góc với đáy, đồng thời \(AC{C^\prime }{A^\prime }\) ' là hình thoi có góc \(\widehat {{A^\prime }AC} = {60^0 }\).
Tính tan góc giữa hai mặt phẳng \(\left( {BC{C^\prime }{B^\prime }} \right)\) và \((ABCD)\).
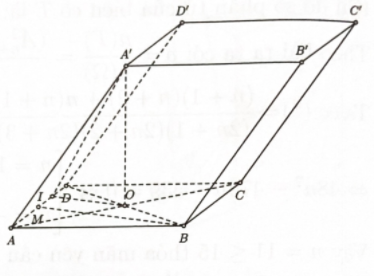
Bước 1: Xác định góc giữa hai mặt phẳng \(\left( {BC{C^\prime }{B^\prime }} \right)\) và \((ABCD)\)
Gọi \(M\) là trung điểm $A D$
\( \Rightarrow BM \bot AD({\mathop{\rm tam}\nolimits} \) giác $A B D$ I$ là trung điểm $M D$
\( \Rightarrow OI \bot AD \Rightarrow \) góc giữa hai mặt phẳng \(\left( {BC{C^\prime }{B^\prime }} \right)\) và \((ABCD)\) bằng \(\widehat {{A^\prime }IO}\).
Bước 2: Tính \(\tan \widehat {{A^\prime }IO}\)
Ta có \(AC = 2AO = 2 \cdot \dfrac{{a\sqrt 3 }}{2} = a\sqrt 3 \).
Xét tam giác \(A{A^\prime }O\) vuông tại \(O\) có: \({A^\prime }O = AO \cdot \tan {60^0 } = \dfrac{{a\sqrt 3 }}{2} \cdot \sqrt 3 = \dfrac{{3a}}{2}\).
Xét \(\Delta BMD\) có: \(OI = \dfrac{1}{2}BM = \dfrac{{a\sqrt 3 }}{4}\).
Xét tam giác \({A^\prime }IO\) vuông tại \(O\) có: \(\tan \widehat {{A^\prime }IO} = \dfrac{{{A^\prime }O}}{{OI}} = 2\sqrt 3 \)
Cho hình hộp \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\) có đáy là hình thoi cạnh \(a\) và góc \(\widehat {BAD} = q\). Mặt chéo \(AC{C^\prime }{A^\prime }\) nằm trong mặt phẳng vuông góc với đáy, đồng thời \(AC{C^\prime }{A^\prime }\) ' là hình thoi có góc \(\widehat {{A^\prime }AC} = {60^0 }\).
Tính thể tích khối tứ diện \(AC{B^\prime }{D^\prime }\).
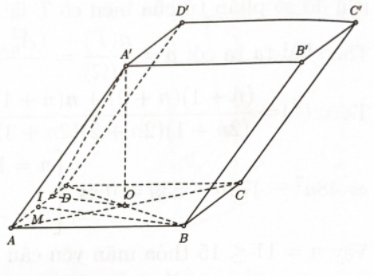
Bước 1: Tính \({S_{ABCD}};A'O\)
Ta có \({S_{ABCD}} = 2{S_{ABD}}\)\( = 2 \cdot \dfrac{1}{2}AB \cdot AD \cdot \sin {60^0 } = \dfrac{{{a^2}\sqrt 3 }}{2};\)\({A^\prime }O = \dfrac{{3a}}{2}\).
Bước 2: Tính \({V_{AC{B^\prime }{D^\prime }}} = \dfrac{1}{3}{V_{ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }}}\)
=> \({V_{AC{B^\prime }{D^\prime }}} = \dfrac{1}{3}{V_{ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }}}\)\( = \dfrac{1}{3} \cdot {A^\prime }O \cdot {S_{ABCD}}\)\( = \dfrac{1}{3} \cdot \dfrac{{3a}}{2} \cdot \dfrac{{{a^2}\sqrt 3 }}{2} = \dfrac{{{a^3}\sqrt 3 }}{4}\)
Cho hình hộp \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\) có đáy là hình thoi cạnh \(a\) và góc \(\widehat {BAD} = q\). Mặt chéo \(AC{C^\prime }{A^\prime }\) nằm trong mặt phẳng vuông góc với đáy, đồng thời \(AC{C^\prime }{A^\prime }\) ' là hình thoi có góc \(\widehat {{A^\prime }AC} = {60^0 }\).
Tính diện toàn phần của hình nón có đáy là đường tròn nội tiếp \(\Delta ABD\) và chiều cao bằng chiều cao của lăng trụ.
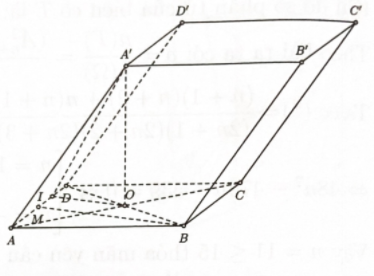
Bước 1: Tính bán kính đường tròn đáy của hình nón.
Vì \(\Delta ABD\) đều nên tâm đường tròn nội tiếp tam giác trùng với trọng tâm của tam giác
\( \Rightarrow \) Bán kính đường tròn đáy của hình nón là: \(r = \dfrac{{BM}}{3} = \dfrac{{a\sqrt 3 }}{6}\).
Bước 2: Tính diện tích xung quanh của hình nón \({S_{xq}} = \pi rl + \pi {r^2}\)
Vì chiều cao của hình nón bằng chiều cao của lăng trụ nên ta có độ dài đường sinh là
\(l = \sqrt {{A^\prime }{O^2} - {r^2}} \)\( = \sqrt {{{\left( {\dfrac{{3a}}{2}} \right)}^2} - {{\left( {\dfrac{{a\sqrt 3 }}{6}} \right)}^2}} = \dfrac{{a\sqrt {159} }}{6}\)
Vậy diện tích xung quanh của hình nón là: \({S_{xq}} = \pi rl + \pi {r^2}\)\( = \dfrac{{\pi {a^2}(\sqrt {53} + 1)}}{{12}}\).
Cho khối nón đỉnh \(S\) có bán kính đáy bằng \(2\sqrt 3 a\). Gọi \(A\) và \(B\) là hai điểm thuộc đường tròn đáy sao cho \(AB = 4a\). Biết khoảng cách từ tâm của đáy đến mặt phẳng \((SAB)\) bằng $2 a$, thể tích của khối nón đã cho bằng
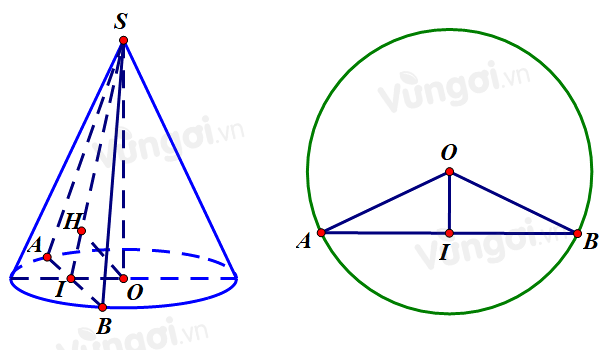
Ta có thể tích của khối nón là \(V = \dfrac{1}{3}{S_d}.h = \dfrac{1}{2}\pi {r^2}h\)
Có \(r = 2\sqrt 3 a\). Ta cần tìm h=SO.
Gọi \(I\) là trung điểm của $A B$.
Khi đó \(\left\{ {\begin{array}{*{20}{l}}{SI \bot AB(\Delta SAB\text{ cân})}\\{OI \bot AB(\Delta OAB\text{ cân})}\end{array} \Rightarrow AB \bot (SOI)} \right.\)
Mà \(AB \subset (SAB) \Rightarrow (SAB) \bot (SOI)\)
Kẻ \(OH \bot SI\). Ta có: \(\left\{ {\begin{array}{*{20}{l}}{(SAB) \bot (SOI)}\\{(SAB) \cap (SOI) = SI \Rightarrow OH \bot (SAB)}\\{OH \bot SI}\end{array}} \right.\)
Suy ra \(d(O,(SAB)) = OH = 2a\)
Xét vuông tại \(I\) ta có:
\(OI = \sqrt {O{A^2} - A{I^2}} = \sqrt {O{A^2} - {{\left( {\dfrac{{AB}}{2}} \right)}^2}} \)\( = \sqrt {{{(2\sqrt 3 a)}^2} - {{\left( {\dfrac{{4a}}{2}} \right)}^2}} = 2\sqrt 2 a\)
Xét vuông tại \(S\) ta có:
\(\dfrac{1}{{O{H^2}}} = \dfrac{1}{{S{O^2}}} + \dfrac{1}{{O{I^2}}}\)
\( \Rightarrow \dfrac{1}{{S{O^2}}} = \dfrac{1}{{O{H^2}}} - \dfrac{1}{{O{I^2}}} = \dfrac{{O{I^2} - O{H^2}}}{{O{H^2} \cdot O{I^2}}}\)
\( \Rightarrow S{O^2} = \dfrac{{O{H^2} \cdot O{I^2}}}{{O{I^2} - O{H^2}}}\)
\( \Rightarrow SO = \dfrac{{OH \cdot OI}}{{\sqrt {O{I^2} - O{H^2}} }}\)\( = \dfrac{{2a \cdot 2\sqrt 2 a}}{{\sqrt {{{(2\sqrt 2 a)}^2} - {{(2a)}^2}} }} = 2\sqrt 2 a\)
Vậy \(V = \dfrac{1}{3}{S_d} \cdot h = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}\pi {(OA)^2}.SO\)\( = \dfrac{1}{3}\pi \cdot {(2\sqrt 3 a)^2} \cdot 2\sqrt 2 a = 8\sqrt 2 \pi {a^3}\).
