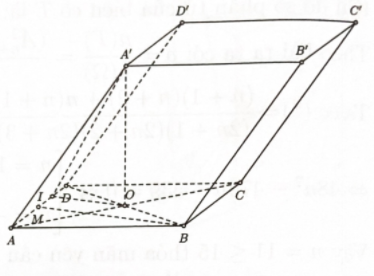
Cho hình hộp $ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }$ có đáy là hình thoi cạnh $a$ và góc $\widehat {BAD} = q$. Mặt chéo $AC{C^\prime }{A^\prime }$ nằm trong mặt phẳng vuông góc với đáy, đồng thời $AC{C^\prime }{A^\prime }$ ' là hình thoi có góc $\widehat {{A^\prime }AC} = {60^0 }$.

Tính diện toàn phần của hình nón có đáy là đường tròn nội tiếp $\Delta ABD$ và chiều cao bằng chiều cao của lăng trụ.

Khối nón có chiều cao bằng bán kính đáy và có thể tích bằng $9\pi$, chiều cao của khối nón đó bằng:

Trong tất cả các hình nón nội tiếp trong hình cầu có thể tích bằng $36\pi$, bán kính $r$ của hình nón có diện tích xung quanh lớn nhất là

Trong không gian, cho hình thang cân $ABCD,\,\,AB//CD,$ $AB = 3a,\,\,CD = 6a,$ đường cao $MN = 2a,$ với $M,\,\,N$ lần lượt là trung điểm cảu $AB$ và $CD.$ Khi quay hình thang cân quang trục đối xứng $MN$ thì được một hình nón cụt có diện tích xung quanh là:

Cho hình lập phương có cạnh bằng $a$. Diện tích toàn phần của hình nón có đỉnh là tâm của một mặt còn đáy là đường tròn nội tiếp mặt đối diện là

Cho khối nón có bán kính đáy $r = \sqrt 3$ và chiều cao $h = 4$. Tính thể tích $V$ của khối nón đã cho.

Cho hình nón S có bán kính $R = a\sqrt 2$, góc ở đỉnh bằng ${60^0}.$ Diện tích toàn phần của hình nón bằng :

Cho khối nón có bán kính đáy bằng 3 và diện tích xung quanh bằng $12\pi$. Hỏi thể tích của khối nón đã cho bằng bao nhiêu?