Hai đường thẳng vuông góc

Vì tia $Om$  nằm giữa hai tia $Ox$  và $Oy.$

$ \Rightarrow \widehat {xOm} + \widehat {mOy} = \widehat {xOy} \Rightarrow {30^0} + \widehat {mOy} = {90^0}$

$ \Rightarrow \widehat {mOy} = {90^0} - {30^0} = {60^0}\,\,\,\,\,$

Trên nửa mặt phẳng bờ chứa tia $Oy$ có : \(\widehat {nOy} < \widehat {mOy}\,\,\left( {{{30}^0} < {{60}^0}} \right)\)

Suy ra tia $On$  nằm giữa hai tia $Om$  và $Oy.$

$ \Rightarrow \widehat {nOy} + \widehat {mOn} = \widehat {mOy} \Rightarrow {30^0} + \widehat {mOn} = {60^0}$

$ \Rightarrow \widehat {mOn} = {60^0} - {30^0} = {30^0}$

$ \Rightarrow \widehat {xOm} = \widehat {mOn} = {30^0}$ và tia $Om$  nằm giữa hai tia $Ox$  và $On.$

Vậy $Om$ là tia phân giác của góc $xOn.$

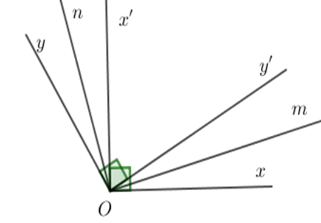
Ta có \(Om\) và $On$ là tia phân giác của các góc $xOy'$ và góc \(x'Oy\) nên \(\widehat {xOm} = \dfrac{{\widehat {xOy'}}}{2} = {15^o};\) \(\widehat {nOy} = \dfrac{{\widehat {x'Oy}}}{2} = {15^o}\)

Lại có \(\widehat {xOm} + \widehat {mOn} + \widehat {nOy} = \widehat {xOy}\) \( \Rightarrow \widehat {mOn} = {90^o} \Rightarrow Om \bot On\)

 Vì \(Ox';Oy'\) nằm giữa hai tia $Ox;Oy$ nên \(\widehat {xOy'} + \widehat {yOy'} = \widehat {xOy}\) \( \Rightarrow \widehat {xOy'} + 90^\circ  = 120^\circ \)\( \Rightarrow \widehat {xOy'} = {30^o}\)  

Tương tự ta có \(\widehat {xOy'} = {30^o}.\)

 Vì \(Ox';Oy'\) nằm giữa hai tia $Ox;Oy$ nên \(\widehat {xOy'} + \widehat {yOy'} = \widehat {xOy}\) \( \Rightarrow \widehat {xOy'} + 90^\circ  = 120^\circ \)\( \Rightarrow \widehat {xOy'} = {30^o}\)  

Tương tự ta có \(\widehat {xOy'} = {30^o}.\)

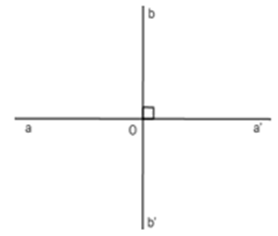
Hai đường thẳng $aa'$  và $bb'$vuông góc với nhau tại $O$  nên :

+) \(\widehat {aOb} = {90^o}\)=> B đúng.

+) aa’ và bb’ vuông góc với nhau nên $aa'$  và $bb'$ cắt nhau => C sai.

+) \(\widehat {a'Ob} = \widehat {a'Ob'} = {90^o}\)=> $aa'$  là đường phân giác của góc bẹt \(bOb'\) => D đúng.

+) \(\widehat {b'Oa'} = {90^o}\)=> A đúng.

Hai đường thẳng vuông góc thì cắt nhau.

Đường trung trực của đoạn thẳng là đường vuông góc với đoạn thẳng ấy tại trung điểm của nó.

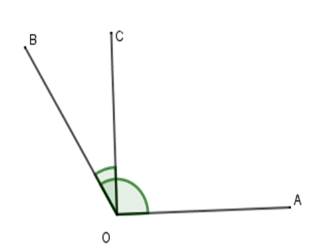
Vì \(OC\) nằm giữa hai tia $OA$ và \(OB\) nên \(\widehat {AOC} + \widehat {COB} = \widehat {AOB}\)\( \Rightarrow \widehat {AOC} + 30^\circ  = 120^\circ \)\( \Rightarrow \widehat {AOC} = 90^\circ \)

Suy ra \(OC \bot OA.\)

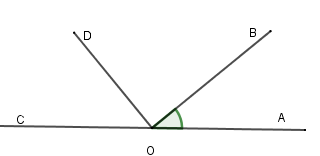
Vì \(OD \bot OB\) nên \(\widehat {DOB} = 90^\circ .\)

Vì \(OA\) và \(OC\) là hai tia đối nhau và tia \(OB\) nằm giữa \(OA\) và \(OD\) nên ta có

\(\widehat {AOB} + \widehat {DOB} + \widehat {COD} = \widehat {AOC}\)\( \Rightarrow 30^\circ  + 90^\circ  + \widehat {COD} = 180^\circ \)\( \Rightarrow \widehat {COD} = 180^\circ  - 120^\circ \)\( \Rightarrow \widehat {COD} = 60^\circ .\)

Vậy \(\widehat {COD} = 60^\circ .\)

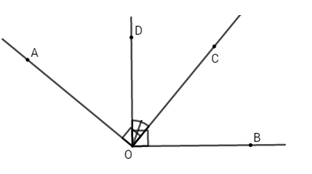
Vì tia OD nằm giữa hai tia OA và OB

\( \Rightarrow \widehat {AOD} + \widehat {DOB} = \widehat {AOB} \)\(\Rightarrow \widehat {AOD} + {90^0} = {140^0}\)

\( \Rightarrow \widehat {AOD} = {140^0} - {90^0} = {50^0}\,\,\,\,\,\,(1)\)

Vì tia OC nằm giữa hai tia OA và OB

$ \Rightarrow \widehat {AOC} + \widehat {COB} = \widehat {AOB}$$ \Rightarrow {90^0} + \widehat {COB} = {140^0}$

$ \Rightarrow \widehat {COB} = {140^0} - {90^0} = {50^0}\,\,\,\,\,\,(2)$

Từ (1) và (2) \( \Rightarrow \widehat {AOD} = \widehat {BOC} = {50^0}\)

Trên nửa mặt phẳng bờ chứa tia OA có : \(\widehat {AOD} < \widehat {AOC}\,\,\left( {{{50}^0} < {{90}^0}} \right)\)

Suy ra tia $OD$  nằm giữa hai tia $OA$  và $OC$

$ \Rightarrow \widehat {AOD} + \widehat {COD} = \widehat {AOC} $$\Rightarrow {50^0} + \widehat {COD} = {90^0}$

$ \Rightarrow \widehat {COD} = {90^0} - {50^0} = {40^0}.$

Vậy \(\widehat {COD} = 40^\circ .\)

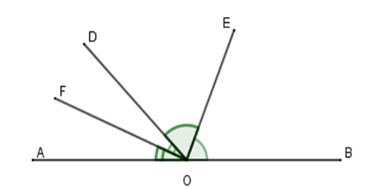
Giả sử \(\widehat {AOD}\) và \(\widehat {DOB}\) là hai góc kề bù, \(OE\) là phân giác \(\widehat {DOB}\) và \(OF\) là phân giác \(\widehat {DOA}.\)

Ta có \(\widehat {AOD} + \widehat {BOD} = 180^\circ \) (tính chất hai góc kề bù)

Vì \(OE\) là phân giác \(\widehat {DOB}\)  nên \(\widehat {BOE} = \widehat {EOD} = \dfrac{{\widehat {DOB}}}{2}\,\,\,\left( 1 \right)\)

Vì \(OF\) là phân giác \(\widehat {DOA}\)  nên \(\widehat {AOF} = \widehat {DOF} = \dfrac{{\widehat {AOD}}}{2}\,\left( 2 \right)\)

Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra \(\widehat {DOF} + \widehat {DOE} = \dfrac{{\widehat {DOA}}}{2} + \dfrac{{\widehat {DOB}}}{2}\) \( = \dfrac{{\widehat {DOA} + \widehat {DOB}}}{2} = \dfrac{{180^\circ }}{2} = 90^\circ \)

Hay \(\widehat {EOF} = 90^\circ  \Rightarrow OE \bot OF\) . Vậy hai tia phân giác của hai góc kề bù thì vuông góc với nhau.

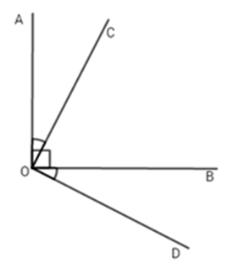
Vì $OC$  nằm giữa tia $OA$  và $OB$ nên:

$\widehat {AOC} + \widehat {COB} = \widehat {AOB}$ mà \(\widehat {AOB} = {90^0}\) (đề bài) \( \Rightarrow \widehat {AOC} + \widehat {COB} = {90^0}\) (*)

Mà \(\widehat {AOC} = \widehat {BOD} \) (đề bài)

nên từ (*) \(\Rightarrow \widehat {BOD} + \widehat {COB} = {90^0}.\, (1)\) 

Lại có tia $OB$  nằm giữa tia $OC$  và $OD$  nên ${\rm{ }}\widehat {BOD} + \widehat {COB} = \widehat {COD}.\, (2)$

Từ (1) và (2) suy ra \(\widehat {COD} = {90^0}.\)

Vậy \(\widehat {COD} = {90^0}.\)

Vì tia $Om$  nằm giữa hai tia $Ox$  và $Oy.$

$ \Rightarrow \widehat {xOm} + \widehat {mOy} = \widehat {xOy} \Rightarrow {30^0} + \widehat {mOy} = {90^0}$

$ \Rightarrow \widehat {mOy} = {90^0} - {30^0} = {60^0}\,\,\,\,\,$

Trên nửa mặt phẳng bờ chứa tia $Oy$ có : \(\widehat {nOy} < \widehat {mOy}\,\,\left( {{{30}^0} < {{60}^0}} \right)\)

Suy ra tia $On$  nằm giữa hai tia $Om$  và $Oy.$

$ \Rightarrow \widehat {nOy} + \widehat {mOn} = \widehat {mOy} \Rightarrow {30^0} + \widehat {mOn} = {60^0}$

$ \Rightarrow \widehat {mOn} = {60^0} - {30^0} = {30^0}$

$ \Rightarrow \widehat {xOm} = \widehat {mOn} = {30^0}$ và tia $Om$  nằm giữa hai tia $Ox$  và $On.$

Vậy $Om$ là tia phân giác của góc $xOn.$

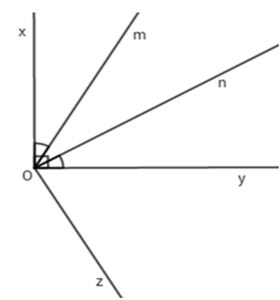
Vì $Oy$  là tia phân giác của góc $mOz$ nên \(\widehat {mOz} = 2.\widehat {mOy} = {2.60^0} = {120^0}\)

Trên nửa mặt phẳng bờ chứa tia $Om$  có: \(\widehat {mOn} < \widehat {mOz}\,\,\left( {{{30}^0} < {{120}^0}} \right)\)

Suy ra tia $On$  nằm giữa hai tia $Om$  và $Oz$

$ \Rightarrow \widehat {mOn} + \widehat {nOz} = \widehat {mOz} \Rightarrow {30^0} + \widehat {nOz} = {120^0}$

$ \Rightarrow \widehat {nOz} = {120^0} - {30^0} = {90^0}$

Vậy $On$  vuông góc với $Oz.$

 Vì \(Ox';Oy'\) nằm giữa hai tia $Ox;Oy$ nên \(\widehat {xOy'} + \widehat {yOy'} = \widehat {xOy}\) \( \Rightarrow \widehat {xOy'} + 90^\circ  = 120^\circ \)\( \Rightarrow \widehat {xOy'} = {30^o}\)  

Tương tự ta có \(\widehat {xOy'} = {30^o}.\)

Ta có \(Om\) và $On$ là tia phân giác của các góc $xOy'$ và góc \(x'Oy\) nên \(\widehat {xOm} = \dfrac{{\widehat {xOy'}}}{2} = {15^o};\) \(\widehat {nOy} = \dfrac{{\widehat {x'Oy}}}{2} = {15^o}\)

Lại có \(\widehat {xOm} + \widehat {mOn} + \widehat {nOy} = \widehat {xOy}\) \( \Rightarrow \widehat {mOn} = {90^o} \Rightarrow Om \bot On\)

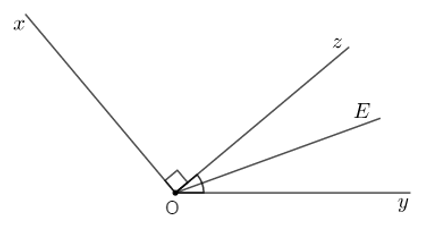
Vì \(OE\) là tia phân giác của \(\widehat {zOy}\) nên \(\widehat {zOE} = \dfrac{1}{2}\widehat {zOy} = {20^0}\) suy ra \(\widehat {zOy} = {2.20^o} = {40^o}.\)

Trên nửa mặt phẳng bờ \(Ox\) có: \(\widehat {xOz} < \widehat {xOy}\,\left( {{{90}^o} < \alpha } \right)\) nên tia \(Oz\) nằm giữa hai tia \(Ox\) và \(Oy\), ta có:

\(\begin{array}{l}\widehat {xOy} = \widehat {xOz} + \widehat {zOy}\\ \Rightarrow \widehat {xOy} = {90^o} + {40^o} = {130^o}\end{array}\)

Vậy \(\widehat {xOy} = {130^o}.\)