Câu hỏi:
3 năm trước
Cho \(\widehat {xOy} = 120^\circ \) vẽ $Ox' \bot Ox;\,Oy' \bot Oy$ sao cho tia \(Ox';Oy'\) nằm giữa hai tia $Ox;Oy.$
Kẻ \(Om\) và $On$ là tia phân giác của các góc $xOy'$ và góc \(x'Oy\). Khi đó
Trả lời bởi giáo viên
Đáp án đúng: a
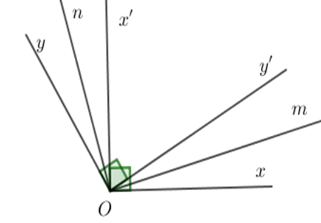
Ta có \(Om\) và $On$ là tia phân giác của các góc $xOy'$ và góc \(x'Oy\) nên \(\widehat {xOm} = \dfrac{{\widehat {xOy'}}}{2} = {15^o};\) \(\widehat {nOy} = \dfrac{{\widehat {x'Oy}}}{2} = {15^o}\)
Lại có \(\widehat {xOm} + \widehat {mOn} + \widehat {nOy} = \widehat {xOy}\) \( \Rightarrow \widehat {mOn} = {90^o} \Rightarrow Om \bot On\)
Hướng dẫn giải:
Sử dụng tính chất góc vuông, tính chất cộng góc.

