Câu hỏi:
2 năm trước
Cho \(\widehat {AOB} = {55^0}.\) Vẽ tia \(OC\) là tia đối của tia \(OA.\) Vẽ tia \(OD\) sao cho \(OD \bot OB,\) và các tia \(OD\), \(OA\) thuộc hai nửa mặt phẳng đối nhau bờ \(OB.\) Chọn câu sai.
Trả lời bởi giáo viên
Đáp án đúng: d
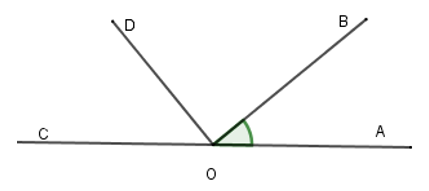
Vì \(OD \bot OB\) nên \(\widehat {DOB} = 90^\circ \) (B đúng).
Tia \(OD\) và \(OA\) thuộc hai nửa mặt phẳng đối nhau bờ \(OB\) nên \(OB\) nằm giữa hai tia \(OA,\,\,OD\), ta có:
\(\widehat {AOD} = \widehat {AOB} + \widehat {DOB} = {55^o} + {90^o} = {145^o}\) (C đúng).
Vì \(OA\) và \(OC\) là hai tia đối nhau nên tia \(OD\) nằm giữa hai tia \(OA\) và \(OC\), ta có:
\(\widehat {AOD} + \widehat {COD} = \widehat {AOC}\)
\( \Rightarrow {145^o} + \widehat {COD} = 180^\circ \)
\( \Rightarrow \widehat {COD} = 180^\circ - 145^\circ = {35^o}\) (A đúng).
Hướng dẫn giải:
Sử dụng tính chất cộng góc và góc bẹt có số đo \(180^\circ .\)
Câu hỏi khác
- Bài tập hai đường thẳng song song. Tiên đề ơ-clit về hai đường thẳng song song toán 7 có lời giải
- Bài tập hai góc đối đỉnh toán 7 có lời giải
- Bài tập mối liên hệ từ vuông góc đến song song toán 7 có lời giải
- Bài tập hai đường thẳng vuông góc toán 7 có lời giải
- Bài tập các góc tạo bởi một đường thẳng cắt hai đường thẳng toán 7 có lời giải
