Câu hỏi:
2 năm trước
Cho góc $AOB$ có số đo bằng $140^o$. Trong góc này vẽ hai tia $OC$ và $OD$ vuông góc với tia $OA$ và $OB.$
So sánh góc $AOD$ và góc $BOC.$
Trả lời bởi giáo viên
Đáp án đúng: c
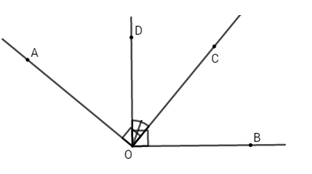
Vì tia OD nằm giữa hai tia OA và OB
\( \Rightarrow \widehat {AOD} + \widehat {DOB} = \widehat {AOB} \)\(\Rightarrow \widehat {AOD} + {90^0} = {140^0}\)
\( \Rightarrow \widehat {AOD} = {140^0} - {90^0} = {50^0}\,\,\,\,\,\,(1)\)
Vì tia OC nằm giữa hai tia OA và OB
$ \Rightarrow \widehat {AOC} + \widehat {COB} = \widehat {AOB}$$ \Rightarrow {90^0} + \widehat {COB} = {140^0}$
$ \Rightarrow \widehat {COB} = {140^0} - {90^0} = {50^0}\,\,\,\,\,\,(2)$
Từ (1) và (2) \( \Rightarrow \widehat {AOD} = \widehat {BOC} = {50^0}\)
Hướng dẫn giải:
Áp dụng tính chất tia nằm giữa hai tia còn lại, cộng góc, tính số đo góc AOD và BOC. Từ đó so sánh hai góc đó.
Câu hỏi khác
- Bài tập hai góc đối đỉnh toán 7 có lời giải
- Bài tập hai đường thẳng song song. Tiên đề ơ-clit về hai đường thẳng song song toán 7 có lời giải
- Bài tập mối liên hệ từ vuông góc đến song song toán 7 có lời giải
- Bài tập hai đường thẳng vuông góc toán 7 có lời giải
- Bài tập các góc tạo bởi một đường thẳng cắt hai đường thẳng toán 7 có lời giải
