Câu hỏi:
2 năm trước
Cho \(\widehat {xOy} = \alpha \,\left( {{{90}^0} < \alpha < {{180}^0}} \right)\). Trên nửa mặt phẳng bờ \(Oy\) có chứa tia \(Ox,\) kẻ \(Oz \bot Ox.\) Gọi \(OE\) là tia phân giác của \(\widehat {zOy}.\) Biết \(\widehat {zOE} = {20^0}.\) Tính \(\widehat {xOy}.\)
Trả lời bởi giáo viên
Đáp án đúng: d
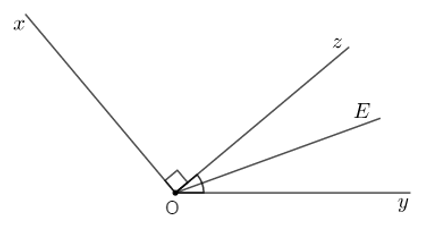
Vì \(OE\) là tia phân giác của \(\widehat {zOy}\) nên \(\widehat {zOE} = \dfrac{1}{2}\widehat {zOy} = {20^0}\) suy ra \(\widehat {zOy} = {2.20^o} = {40^o}.\)
Trên nửa mặt phẳng bờ \(Ox\) có: \(\widehat {xOz} < \widehat {xOy}\,\left( {{{90}^o} < \alpha } \right)\) nên tia \(Oz\) nằm giữa hai tia \(Ox\) và \(Oy\), ta có:
\(\begin{array}{l}\widehat {xOy} = \widehat {xOz} + \widehat {zOy}\\ \Rightarrow \widehat {xOy} = {90^o} + {40^o} = {130^o}\end{array}\)
Vậy \(\widehat {xOy} = {130^o}.\)
Hướng dẫn giải:
- Sử dụng tính chất của tia phân giác tính số đo \(\widehat {zOy}\).
- Chứng minh \(Oz\) nằm giữa hai tia \(Ox\) và tia \(Oy\), từ đó tính \(\widehat {xOy}.\)
Câu hỏi khác
- Bài tập hai đường thẳng song song. Tiên đề ơ-clit về hai đường thẳng song song toán 7 có lời giải
- Bài tập hai góc đối đỉnh toán 7 có lời giải
- Bài tập mối liên hệ từ vuông góc đến song song toán 7 có lời giải
- Bài tập hai đường thẳng vuông góc toán 7 có lời giải
- Bài tập các góc tạo bởi một đường thẳng cắt hai đường thẳng toán 7 có lời giải
