Định luật Bôilơ - Mariốt. Đường đẳng nhiệt

A - sai vì: ${p_1}{V_1} = {p_2}{V_2}$

B - đúng

C, D - sai vì: $pV = const$

A, B, D - đúng

C - sai vì: Áp suất và thể tích tỉ lệ nghịch với nhau

Đường biểu diễn sự biến thiên của áp suất theo thể tích khi nhiệt độ không đổi gọi là đường đẳng nhiệt.

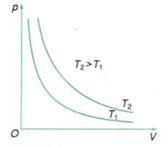
Trong hệ tọa độ (p,V) đường đẳng nhiệt là đường hypebol

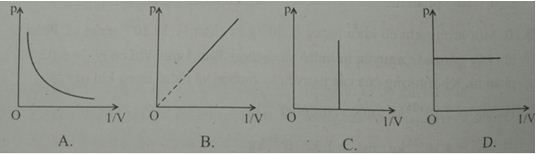
Ta có: $pV = h/s = a \to p = \dfrac{a}{V}$

Tương đương với dạng: $y =ax$

=>Hình B diễn tả đúng định luật Bôilơ - Mariốt

Trạng thái 1:${p_1} = 3{\rm{a}}tm,{V_1} = 10l$

Trạng thái 2: ${p_2} = 6{\rm{a}}tm$

Áp dụng định luật Bôilơ - Mariốt, ta có: ${p_1}{V_1} = {p_2}{V_2} \to {V_2} = \frac{{{p_1}{V_1}}}{{{p_2}}} = \frac{{3.10}}{6} = 5l$

Ta có:

Trạng thái 1: ở điều kiện tiêu chuẩn: ${p_1} = 1{\rm{a}}tm,{t_1} = {0^0}C,\rho  = 1,43kg/{m^3}$

Trạng thái 2: ${V_2} = 6l,{p_2} = 150{\rm{a}}tm,{t_2} = {0^0}C$

+ Áp dụng định luật Bôilơ - Mariốt, ta có: ${p_1}{V_1} = {p_2}{V_2} \to {V_1} = \frac{{{p_2}{V_2}}}{{{p_1}}} = \frac{{150.6}}{1} = 900l = 0,9{m^3}$

+ Khối lượng của khí là: $m = \rho V = 1,43.0,9 = 1,287kg$

Giả sử ban áp suất và thể tích ban đầu của khối khí là: ${p_1},{V_1}$

+ Trạng thái 1: Trạng thái  ban đầu: ${p_1},{V_1}$

+ Trạng thái 2: Trạng thái khi áp suất tăng thêm một lượng ${5.10^5}Pa$

 Ta có: ${p_2} = {p_1} + {5.10^5}Pa,{V_2} = {V_1} - 5$

+ Trạng thái 3: Trạng thái khi áp suất tăng thêm một lượng ${2.10^5}Pa$

Ta có: ${p_3} = {p_1} + {2.10^5}Pa,{V_3} = {V_1} - 3$

Áp dụng định luật Bôilơ - Mariốt cho cả 3 trạng thái, ta có:

$\begin{array}{l}{p_1}{V_1} = {p_2}{V_2} = {p_3}{V_3}\\ \leftrightarrow {p_1}{V_1} = \left( {{p_1} + {{5.10}^5}} \right)\left( {{V_1} - 5} \right) = \left( {{p_1} + {{2.10}^5}} \right)\left( {{V_1} - 3} \right)\\ \to \left\{ \begin{array}{l}{p_1} = {4.10^5}Pa\\{V_1} = 9l\end{array} \right.\end{array}$

Ta có:

+ Thể tích khí bơm vào bóng sau 60 lần bơm là: $V = 60.50 = 3000c{m^3} = 3l$

+ Trạng thái 1: ${V_1} = 2 + 3 = 5l,{p_1} = 1{\rm{a}}tm$

+ Trạng thái 2: ${V_2} = 2l,{p_2} = ?$  \({V_1} = 2l

Áp dụng định luật Bôilơ - Mariốt, ta có: ${p_1}{V_1} = {p_2}{V_2} \to {p_2} = \frac{{{p_1}{V_1}}}{{{V_2}}} = \frac{{1.5}}{2} = 2,5{\rm{a}}tm$

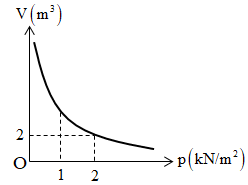
Áp dụng định luật Bôilơ – Mariốt ta có:

${p_1}{V_1} = {p_2}{V_2} \Rightarrow {V_2} = \dfrac{{{p_1}{V_1}}}{{{p_2}}} = \dfrac{{2.2}}{1} = 4\left( {{m^3}} \right)$

Áp dụng định luật Boilo – Mariot ta có:

${p_1}{V_1} = {p_2}{V_2} \Rightarrow {V_2} = \dfrac{{{p_1}{V_1}}}{{{p_2}}} = \dfrac{{{{10}^5}.10}}{{1,{{25.10}^5}}} = 8l$