Trong không gian Oxyz, cho hai đường thẳng chéo nhau \({d_1}:\dfrac{{x - 2}}{2} = \) \(\dfrac{{y - 6}}{{ - 2}} = \dfrac{{z + 2}}{1}\) và \({d_2}:\dfrac{{x - 4}}{1} = \dfrac{{y + 1}}{3} = \dfrac{{z + 2}}{{ - 2}}\). Phương trình mặt phẳng \((P)\) chứa \({d_1}\) và \((P)\) song song với đường thẳng \({d_2}\) là
Bước 1: Tìm vecto chỉ phương của \({d_1}\) và \({d_2}\)
Đường thẳng \({d_1}\) đi qua \(A(2;6; - 2)\) và có một vectơ chỉ phương \({\vec u_1} = (2; - 2;1)\).
Đường thẳng \({d_2}\) có một vectơ chỉ phương \({\vec u_2} = (1;3; - 2)\).
Bước 2: Viết phương trình mặt phẳng
Gọi \(\vec n\) là một vectơ pháp tuyến của mặt phẳng \((P)\). Do mặt phẳng \((P)\) chứa \({d_1}\) và \((P)\) song song với đường thẳng \({d_2}\) nên \(\vec n = \left[ {{{\vec u}_1},{{\vec u}_2}} \right] = (1;5;8)\).
Vậy phương trình mặt phẳng \((P)\) đi qua \(A(2;6; - 2)\) và có một vectơ pháp tuyến \(\vec n = (1;5;8)\) là \(x + 5y + 8z - 16 = 0\).
Trong không gian \(Oxyz\), gọi \(M'\) là điểm đối xứng của điểm \(M\left( { - 1;0;3} \right)\) qua đường thẳng \(d:\dfrac{{x + 1}}{2} = \dfrac{{y - 2}}{3} = \dfrac{{z - 3}}{1}\). Tính khoảng cách từ điểm \(M'\) đến mặt phẳng \(\left( {Oxy} \right)\).
Điền số nguyên hoặc phân số dạng a/b
Đáp án:
Đáp án:
Đường thẳng \(d\) có vectơ chỉ phương \({\vec u_d} = \left( {2;3;1} \right)\).
Gọi \(\left( P \right)\) là mặt phẳng đi qua điểm \(M\left( { - 1;0;3} \right)\) và vuông góc với \(d\).
Khi đó mặt phẳng \(\left( P \right)\) nhận vectơ \({\vec u_d} = \left( {2;3;1} \right)\) làm vectơ pháp tuyến.
\( \Rightarrow \) Phương trình mặt phẳng \(\left( P \right)\): \(2\left( {x + 1} \right) + 3\left( {y - 0} \right) + 1\left( {z - 3} \right) = 0\)
\( \Leftrightarrow 2x + 3y + z - 1 = 0\).
Phương trình tham số của \(d\): \(\left\{ \begin{array}{l}x = - 1 + 2t\\y = 2 + 3t\\z = 3 + t\end{array} \right.\)
Gọi \(H\) là giao điểm của đường thẳng \(d\) và mặt phẳng \(\left( P \right)\).
Ta có \(H \in d\). Suy ra tọa độ \(H\left( { - 1 + 2t;2 + 3t;3 + t} \right)\).
Lại có \(H \in \left( P \right)\). Suy ra \(2\left( { - 1 + 2t} \right) + 3\left( {2 + 3t} \right) + \left( {3 + t} \right) - 1 = 0\)
\( \Leftrightarrow 14t + 6 = 0\)
\( \Leftrightarrow t = - \dfrac{3}{7}\).
Khi đó tọa độ \(H\left( { - \dfrac{{13}}{7};\dfrac{5}{7};\dfrac{{18}}{7}} \right)\).
Vì \(M'\) là điểm đối xứng của \(M\) qua \(d\) nên \(H\) là trung điểm của \(MM'\).
\( \Rightarrow \left\{ \begin{array}{l}{x_H} = \dfrac{{{x_M} + {x_{M'}}}}{2}\\{y_H} = \dfrac{{{y_M} + {y_{M'}}}}{2}\\{z_H} = \dfrac{{{z_M} + {z_{M'}}}}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - \dfrac{{13}}{7} = \dfrac{{ - 1 + {x_{M'}}}}{2}\\\dfrac{5}{7} = \dfrac{{0 + {y_{M'}}}}{2}\\\dfrac{{18}}{7} = \dfrac{{3 + {z_{M'}}}}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_{M'}} = - \dfrac{{19}}{7}\\{y_{M'}} = \dfrac{{10}}{7}\\{z_{M'}} = \dfrac{{15}}{7}\end{array} \right.\)
\( \Rightarrow \) Tọa độ \(M'\left( { - \dfrac{{19}}{7};\dfrac{{10}}{7};\dfrac{{15}}{7}} \right)\).
Trục \(\left( {Oxy} \right)\): \(z = 0\).
Khoảng cách từ điểm \(M'\) đến mặt phẳng \(\left( {Oxy} \right)\) là: \(d\left( {M',\left( {Oxy} \right)} \right) = \dfrac{{\left| {\dfrac{{15}}{7}} \right|}}{{\sqrt {{1^2}} }} = \dfrac{{15}}{7}\).
Vậy khoảng cách từ điểm \(M'\) đến mặt phẳng \(\left( {Oxy} \right)\) bằng \(\dfrac{{15}}{7}\).
Đề thi THPT QG - 2021 - mã 101
Trong không gian \({\rm{Ox}}yz\), cho hai điểm \(A(1;0;0)\)và \(B(4;1;2)\). Mặt phẳng đi qua \(A\) và vuông góc với \(AB\) có phương trình là:
Gọi \(\left( P \right)\) là mặt phẳng cần tìm ta có: \(\left( P \right) \bot AB \Rightarrow \overrightarrow {{n_P}} = \overrightarrow {AB} = \left( {3;1;2} \right)\).
\( \Rightarrow \) Phương trình \(\left( P \right):\,\,3\left( {x - 1} \right) + y + 2z = 0\) \( \Leftrightarrow 3x + y + 2z - 3 = 0\).
Trong không gian \(Oxyz,\) cho đường thẳng \(d:\,\,\dfrac{{x - 2}}{{ - 1}} = \dfrac{{y - 1}}{2} = \dfrac{z}{2}\) và mặt phẳng \(\left( P \right):\,\,x + 2y - z - 5 = 0.\) Tọa độ giao điểm của \(d\) và \(\left( P \right)\) là:
Ta có: \(d:\,\,\dfrac{{x - 2}}{{ - 1}} = \dfrac{{y - 1}}{2} = \dfrac{z}{2} \Rightarrow d:\,\,\,\left\{ \begin{array}{l}x = 2 - t\\y = 1 + 2t\\z = 2t\end{array} \right. \Rightarrow M\left( {2 - t;\,1 + 2t;\,2t} \right)\) là một điểm thuộc đường thẳng \(d.\)
\(\begin{array}{l}M = d \cap \left( P \right) \Rightarrow 2 - t + 2\left( {1 + 2t} \right) - \left( {2t} \right) - 5 = 0\\ \Leftrightarrow t = 1 \Rightarrow M\left( {1;\,\,3;\,\,2} \right).\end{array}\)
Đề thi THPT QG - 2021 - mã 101
Trong không gian \(Oxyz,\) cho đường thẳng \(d:\dfrac{x}{1} = \dfrac{{y - 1}}{1} = \dfrac{{z - 2}}{{ - 1}}\) và mặt phẳng \(\left( P \right):\,x + 2y + z - 4 = 0\). Hình chiếu vuông góc của \(d\) trên \(\left( P \right)\) là đường thẳng có phương trình:
* Nhận thấy \(I\left( {0;1;2} \right) \in d\) và cũng thuộc \(\left( P \right)\).
\( \Rightarrow d \cap \left( P \right) = I\left( {0;1;2} \right)\).
Gọi \(d'\) là hình chiếu của \(d\) trên \(\left( P \right) \Rightarrow I \in d'\).
* Lấy \(A\left( {1;2;1} \right) \in d\).
Gọi \(\Delta \) là đường thẳng qua \(A\) và vuông góc với \(\left( P \right)\) \( \Rightarrow \overrightarrow {{u_\Delta }} = \overrightarrow {{n_{\left( P \right)}}} = \left( {1;2;1} \right)\).
\( \Rightarrow \) Phương trình đường thẳng \(\Delta :\,\,\left\{ \begin{array}{l}x = 1 + 2t\\y = 2 + 2t\\z = 1 + t\end{array} \right.\).
Gọi \(H = \Delta \cap \left( P \right) \Rightarrow H \in \Delta \Rightarrow H\left( {1 + t;\,\,2 + 2t;\,\,1 + t} \right)\).
Mà \(H \in \left( P \right) \Rightarrow \left( {1 + t} \right) + 2\left( {2 + 2t} \right) + \left( {1 + t} \right) - 4 = 0\)\( \Leftrightarrow 6t + 2 = 0 \Leftrightarrow t = - \dfrac{1}{3}\).
\( \Rightarrow H\left( {\dfrac{2}{3};\dfrac{4}{3};\dfrac{2}{3}} \right)\).
* \(d'\) là đường thẳng đi qua \(I\) và \(H\).
Ta có \(\overrightarrow {IH} = \left( {\dfrac{2}{3};\dfrac{1}{3}; - \dfrac{4}{3}} \right) \Rightarrow \overrightarrow {{u_{d'}}} = 3\overrightarrow {IH} = \left( {2;1; - 4} \right)\).
\( \Rightarrow \) Phương trình đường thẳng \(d':\,\,\dfrac{x}{2} = \dfrac{{y - 1}}{1} = \dfrac{{z - 2}}{{ - 4}}\).
Trong không gian Oxyz, mặt phẳng đi qua điểm \(A\left( {1;2; - 3} \right)\) và vuông góc với đường thẳng \(d:\,\,\dfrac{{x - 3}}{2} = \dfrac{{y + 1}}{{ - 1}} = \dfrac{{z - 2}}{3}\) có phương trình là:
Đường thẳng \(d:\,\,\dfrac{{x - 3}}{2} = \dfrac{{y + 1}}{{ - 1}} = \dfrac{{z - 2}}{3}\) có 1 VTCP là \(\overrightarrow u \left( {2; - 1;3} \right)\)
Vì \(\left( P \right) \bot d \Rightarrow \overrightarrow {{n_P}} = \overrightarrow {{u_d}} \left( {2; - 1;3} \right)\)
Vậy phương trình mặt phẳng (P) là: \(2x - y + 3z + 9 = 0\).
Trong không gian \(Oxyz\), cho hai đường thẳng \(d:\,\,\left\{ \begin{array}{l}x = - 1 - 2t\\y = t\\z = - 1 + 3t\end{array} \right.,\,\,d':\,\,\left\{ \begin{array}{l}x = 2 + t'\\y = - 1 + 2t'\\z = - 2t'\end{array} \right.\) và mặt phẳng \(\left( P \right):\,\,x + y + z + 2 = 0\). Đường thẳng vuông góc với mặt phẳng \(\left( P \right)\) và cắt hai đường thẳng \(d,\,\,d'\) có phương trình là:
Gọi \(\Delta \) là đường thẳng cần tìm.
Giả sử \(A = \Delta \cap d \Rightarrow A\left( { - 1 - 2t;t; - 1 + 3t} \right)\).
\(B = \Delta \cap d' \Rightarrow B\left( {2 + t'; - 1 + 2t'; - 2t'} \right)\).
\( \Rightarrow \overrightarrow {AB} = \left( {2t + t' + 3; - t + 2t' - 1; - 3t - 2t' + 1} \right)\) là 1 VTCP của \(\Delta \).
\(\left( P \right)\) nhận\(\overrightarrow n \left( {1;1;1} \right)\) là 1 VTPT.
Do \(\Delta \bot \left( P \right) \Rightarrow \overrightarrow {AB} \) và \(\overrightarrow n \) là 2 vectơ cùng phương.
\( \Rightarrow 2t + t' + 3 = - t + 2t' - 1 = - 3t - 2t' + 1 \Leftrightarrow \left\{ \begin{array}{l}3t - t' + 4 = 0\\2t + 4t' - 2 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}t = - 1\\t' = 1\end{array} \right.\)
\( \Rightarrow A\left( {1; - 1; - 4} \right),\,\,B\left( {3;1; - 2} \right) \Rightarrow \overrightarrow {AB} = \left( {2;2;2} \right)//\left( {1;1;1} \right)\).
Vậy phương trình đường thẳng \(\Delta :\,\,\dfrac{{x - 3}}{1} = \dfrac{{y - 1}}{1} = \dfrac{{z + 2}}{1}\).
Trong không gian với hệ tọa độ $Ox y z$, cho tứ diện $ABCD$ có \(A( - 1;1;6)\), \(B( - 3; - 2; - 4),C(1;2; - 1),D(2; - 2;0)\). Điểm \(M(a;b;c)\) thuộc đường thẳng $CD$ sao cho tam giác $AB M$ có chu vi nhỏ nhất. Tính \(a + b + c\).
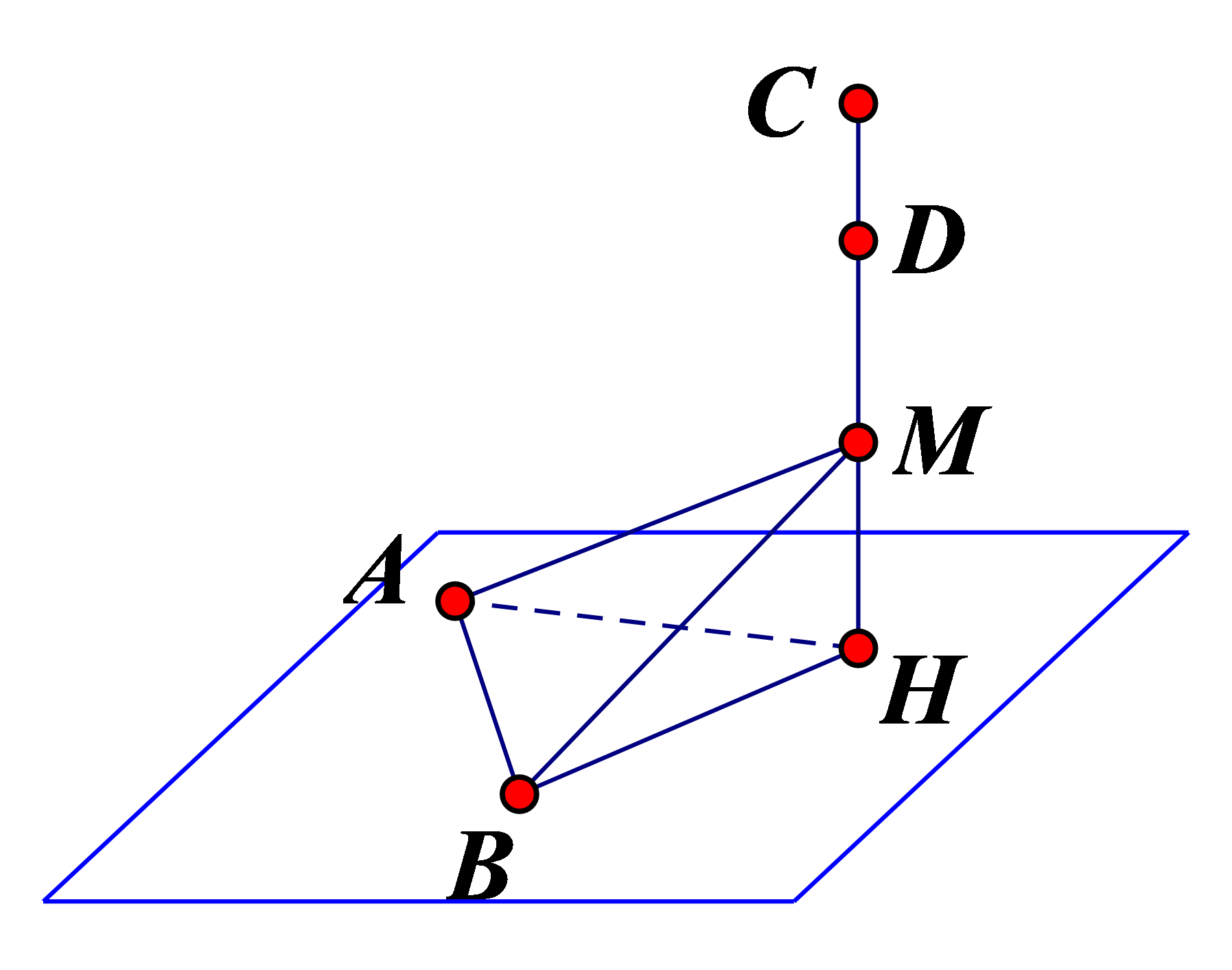
Bước 1: Gọi \({C_{ABM}}\) là chu vi của tam giác $AB M$. Chứng minh \(AB \bot CD\).
Gọi \({C_{ABM}}\) là chu vi của tam giác ABM.
\(\overrightarrow {AB} = ( - 2; - 3; - 10) \Rightarrow AB = \sqrt {113} \)
\(\overrightarrow {AB} = ( - 2; - 3; - 10),\overrightarrow {CD} = (1; - 4;1)\)
\( \Rightarrow \overrightarrow {AB} \cdot \overrightarrow {CD} = - 2 + 12 - 10 = 0 \Rightarrow AB \bot CD\)
Bước 2: Gọi \((P)\) là mặt phẳng chứa đường thẳng $AB$ và vuông vuông góc với đường thẳng $CD$ ; $H$ là giao điểm của \((P)\) và đường thẳng $CD$. Tìm $H$.
Gọi \((P)\) là mặt phẳng chứa đường thẳng $AB$và vuông vuông góc với đường thẳng $CD$ ; $H$ là giao điểm của \((P)\) và đường thẳng $CD$.
Phương trình mặt phẳng \((P)\) qua \(A( - 1;1;6)\) có véctơ pháp tuyến \(\overrightarrow {CD} = (1; - 4;1)\) là \(1 - 4y + z - 1 = 0\)
Vì \(H \in CD\) nên \(H(1 + t;2 - 4t; - 1 + t)\)
Mà \(H \in (P)\)\( \Leftrightarrow 1 + t - 4(2 - 4t) - 1 + t - 1 = 0\)\( \Leftrightarrow t = \dfrac{1}{2} \Leftrightarrow H\left( {\dfrac{3}{2};0; - \dfrac{1}{2}} \right)\).
Bước 3: Tìm điều kiện của $M$ để \({C_{ABM}}\) min, từ đó tính $a+b+c$.
\(\forall M \in CD\), ta có \(\left\{ {\begin{array}{*{20}{l}}{AM \ge AH}\\{BM \ge BH}\end{array}} \right.\)\( \Rightarrow AM + BM \ge AH + BH\)
\({C_{ABM}} = AB + AM + BM\)\( \ge \sqrt {113} + AH + BH,\forall M \in CD\)
Suy ra \(\min {C_{ABM}} = \sqrt {113} + AH + BH\), đạt được \(M \equiv H \Leftrightarrow M\left( {\dfrac{3}{2};0; - \dfrac{1}{2}} \right)\).
Vậy \(a + b + c = 1\).
Đề thi THPT QG - 2021 - mã 102
Trong không gian \(Oxyz,\) cho hai đểm \(A\left( {0;0;1} \right)\) và \(B\left( {2;1;3} \right)\). Mặt phẳng đi qua \(A\) và vuông góc với \(AB\) có phương trình là:
Ta có: \(\overrightarrow {AB} = \left( {2;1;2} \right)\)
Phương trình mặt phẳng đi qua \(A\) và vuông góc với \(AB\) là: \(2\left( {x - 0} \right) + 1\left( {y - 0} \right) + 2\left( {z - 1} \right) = 0 \Leftrightarrow 2x + y + 2z - 2 = 0\)
Đề thi THPT QG - 2021 - mã 102
Trong không gian \(Oxyz,\) cho điểm \(M\left( {2;1; - 1} \right)\) và mặt phẳng \(\left( P \right):x - 3y + 2z + 1 = 0\). Đường thẳng đi qua \(M\) và vuông góc với \(\left( P \right)\) có phương trình là:
Ta có \({\overrightarrow n _{\left( P \right)}} = \left( {1; - 3;2} \right)\)\( = {\overrightarrow u _d}\)
Đường thẳng đi qua điểm \(M\left( {2;1; - 1} \right)\) và có vtcp \(\overrightarrow u = \left( {1; - 3;2} \right)\) sẽ có phương trình chính tắc là:
\(\dfrac{{x - 2}}{1} = \dfrac{{y - 1}}{{ - 3}} = \dfrac{{z + 1}}{2}\)
Đề thi THPT QG 2020 – mã đề 104
Trong gian gian \(Oxyz,\) cho điểm \(M\left( {3; - 2;2} \right)\) và đường thẳng \(d:\dfrac{{x - 3}}{1} = \dfrac{{y + 1}}{2} = \dfrac{{z - 1}}{{ - 2}}\). Mặt phẳng đi qua \(M\) và vuông góc với \(d\) có phương trình là
Ta có: \(d:\dfrac{{x - 3}}{1} = \dfrac{{y + 1}}{2} = \dfrac{{z - 1}}{{ - 2}}\) có VTCP \(\overrightarrow {{u_d}} = \left( {1;\,\,2; - 2} \right).\)
Mặt phẳng \(\left( \alpha \right)\) cần tìm vuông góc với \(d\) \( \Rightarrow \overrightarrow {{n_\alpha }} = \overrightarrow {{u_d}} = \left( {1;\,\,2; - 2} \right).\)
\( \Rightarrow \left( \alpha \right):\,\,\,x - 3 + 2\left( {y + 2} \right) - 2\left( {z - 2} \right) = 0\) \( \Leftrightarrow x + 2y - 2z + 5 = 0\).
Trong không gian \(Oxyz\), cho mặt phẳng \(\left( P \right):x + 2y + 3 = 0\). Đường thẳng \(\Delta \) qua \(A\left( {1;2; - 3} \right)\) vuông góc với mặt phẳng \(\left( P \right)\) có phương trình là
Đường thẳng \(\Delta \) qua \(A\left( {1;2; - 3} \right)\) vuông góc với mặt phẳng \(\left( P \right)\) nhận \(\overrightarrow n = \left( {1;2;0} \right)\) làm VTCP, có phương trình là
\(\left\{ \begin{array}{l}x = 1 + t\\y = 2 + 2t\\z = - 3\end{array} \right.\)
Đề thi THPT QG - 2021 - mã 102
Trong không gian \(Oxyz,\) cho đường thẳng \(d:\dfrac{{x + 1}}{1} = \dfrac{y}{1} = \dfrac{{z - 1}}{2}\) và mặt phẳng \(\left( P \right):2x + y - z + 3 = 0\). Hình chiếu vuông góc của \(d\) trên \(\left( P \right)\) là đường thẳng có phương trình:
Gọi giao điểm của đường thẳng \(d\) và mặt phẳng \(\left( P \right)\) là điểm \(I.\)
Do \(I \in d \Rightarrow I\left( { - 1 + t;t;1 + 2t} \right)\). Mà \(I \in \left( P \right)\)
\( \Rightarrow 2\left( { - 1 + t} \right) + t - \left( {1 + 2t} \right) + 3 = 0 \Rightarrow - 2 + 2t + t - 1 - 2t + 3 = 0 \Rightarrow t = 0\)\( \Rightarrow I\left( { - 1;0;1} \right)\)
Lấy \(A\left( {1;2;5} \right) \in d\)
Gọi \(\Delta \) là đường thẳng qua \(A\) và vuông góc với \(\left( P \right) \Rightarrow {\overrightarrow u _\Delta } = {\overrightarrow n _{\left( P \right)}} = \left( {2;1; - 1} \right)\)
Phương trình đường thẳng \(\Delta :\left\{ \begin{array}{l}x = 1 + 2t\\y = 2 + t\\z = 5 - t\end{array} \right.\)
Gọi \(H\) là giao điểm của \(\Delta \) và \(\left( P \right) \Rightarrow H\left( {1 + 2t;2 + t;5 - t} \right)\)
Mà \(H \in \left( P \right) \Rightarrow 2\left( {1 + 2t} \right) + 2 + t - \left( {5 - t} \right) + 3 = 0 \Rightarrow 6t = - 2 \Rightarrow t = - \dfrac{1}{3}\)\( \Rightarrow H\left( {\dfrac{1}{3};\dfrac{5}{3};\dfrac{{16}}{3}} \right)\)
Ta có: \(\overrightarrow {IH} = \left( {\dfrac{4}{3};\dfrac{5}{3};\dfrac{{13}}{3}} \right)\)
Phương trình đường thẳng \(d'\) qua \(I\) và nhận \(3\overrightarrow {IH} \) làm vtcp: \(\dfrac{{x + 1}}{4} = \dfrac{y}{5} = \dfrac{{z - 1}}{{13}}\)
Trong không gian với hệ tọa độ \(Oxyz\), cho điểm \(A\left( {1; - 1; - 2} \right)\) và mặt phẳng \(\left( P \right):\,\,x - 2y - 3z + 4 = 0\). Viết phương trình đường thẳng đi qua \(A\) và vuông góc với \(\left( P \right)\).
Mặt phẳng \(\left( P \right):\,\,x - 2y - 3z + 4 = 0\) có 1 vecto chỉ phương là \(\overrightarrow {{n_P}} = \left( {1; - 2; - 3} \right)\).
Gọi \(d\) là đường thẳng đi qua \(A\left( {1; - 1; - 2} \right)\) và vuông góc với \(\left( P \right)\) và \(\overrightarrow {{u_d}} \) là 1 vecto chỉ phương của đường thẳng \(d\).
Vì \(d \bot \left( P \right)\) nên \(\overrightarrow {{u_d}} = \overrightarrow {{n_P}} = \left( {1; - 2; - 3} \right)\).
Vậy phương trình đường thẳng \(d\) là \(\dfrac{{x - 1}}{1} = \dfrac{{y + 1}}{{ - 2}} = \dfrac{{z + 2}}{{ - 3}}\).
Cho đường thẳng \(d\) có VTCP \(\overrightarrow u \) và mặt phẳng \(\left( P \right)\) có VTPT \(\overrightarrow n \). Nếu \(\overrightarrow u \bot \overrightarrow n \) và một điểm thuộc \(d\) cũng thuộc \(\left( P \right)\) thì:
Ta có: \(d \subset \left( P \right) \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow u \bot \overrightarrow n \\M \in d,M \in \left( P \right)\end{array} \right.\).
Do đó nếu \(\overrightarrow u \bot \overrightarrow n \) thì \(d//\left( P \right)\) hoặc \(d \subset \left( P \right)\). Ngoài ra nếu \(M \in d\) và \(M \in \left( P \right)\) thì \(d \subset \left( P \right)\).
Trong không gian với hệ tọa độ \(Oxyz\), cho ba điểm \(A\left( {0;0;1} \right)\), \(B\left( { - 1; - 2;0} \right)\) và \(C\left( {2;1; - 1} \right)\). Đường thẳng \(\Delta \) đi qua trọng tâm \(G\) của tam giác \(ABC\) và vuông góc với mặt phẳng \(\left( {ABC} \right)\) có phương trình là:
Gọi \(G\) là trọng tâm của tam giác \(ABC\), suy ra \(G\left( {\dfrac{1}{3}; - \dfrac{1}{3};0} \right)\).
Ta có \(\overrightarrow {AB} = \left( { - 1; - 2; - 1} \right);\,\,\overrightarrow {AC} = \left( {2;1; - 2} \right)\)
Đường thẳng \(\Delta \) vuông góc với mp \(\left( {ABC} \right)\) nên có VTCP \(\overrightarrow u = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( {5; - 4;3} \right)\).
Vậy phương trình \(\Delta \) là: \(\left\{ \begin{array}{l}x = \dfrac{1}{3} + 5t\\y = - \dfrac{1}{3} - 4t\\z = 3t\end{array} \right.\)
Tọa độ giao điểm của đường thẳng d có phương trình $d:\dfrac{{x + 1}}{1} = \dfrac{y}{{ - 1}} = \dfrac{{z + 2}}{3}$ với mặt phẳng (P) có phương trình $(P):x + 2y - z - 3 = 0$ là:
Giả sử M là giao điểm của (d) và (P).
$d:\dfrac{{x + 1}}{1} = \dfrac{y}{{ - 1}} = \dfrac{{z + 2}}{3} \Rightarrow d:\left\{ \begin{array}{l}x = - 1 + t\\y = 0 - t\\z = - 2 + 3t\end{array} \right.$
Lấy \(M \in (d) \Rightarrow M\left( { - 1 + t; - t; - 2 + 3t} \right)\)
Vì \(M \in (P) \Rightarrow - 1 + t + 2.( - t) - ( - 2 + 3t) - 3 = 0 \Leftrightarrow - 4t - 2 = 0 \Leftrightarrow t = - \dfrac{1}{2}\)
Suy ra ta có \(M\left( { - \dfrac{3}{2};\dfrac{1}{2}; - \dfrac{7}{2}} \right)\)
Trong không gian với hệ tọa độ \(Oxyz\), cho đường thẳng \(d:\left\{ \begin{array}{l}x = 1 - t\\y = 2 + t\\z = - t\end{array} \right.\) và mặt phẳng \(\left( \alpha \right):x + y + z - 1 = 0\). Vị trí tương đối của \(d\) và \(\left( \alpha \right)\) là:
Đường thẳng \(d\) có VTCP \(\overrightarrow {{u_d}} = \left( { - 1;1; - 1} \right)\). Mặt phẳng \(\left( \alpha \right)\) có VTPT \(\overrightarrow {{n_\alpha }} = \left( {1;1;1} \right)\).
Ta có \(\overrightarrow {{u_d}} .\overrightarrow {{n_\alpha }} = - 1 + 1 - 1 = - 1 \ne 0\). Suy ra đường thẳng \(d\) cắt mặt phẳng \(\left( \alpha \right)\).
Trong không gian với hệ tọa độ \(Oxyz\), cho mặt phẳng \(\left( P \right):9x + 3y - 10z + 26 = 0\) và đường thẳng \(d:\dfrac{{x + 1}}{2} = \dfrac{{y - 1}}{4} = \dfrac{{z - 2}}{3}\). Mệnh đề nào sau đây là đúng?
Đường thẳng \(d\) đi qua \(M\left( { - 1;1;2} \right)\) và có VTCP \(\overrightarrow {{u_d}} = \left( {2;4;3} \right)\).
Mặt phẳng \(\left( P \right)\) có VTPT \(\overrightarrow {{n_P}} = \left( {9;3; - 10} \right)\) .
+) \(\overrightarrow {{u_d}} .\overrightarrow {{n_P}} = 2.9 + 4.3 + 3.\left( { - 10} \right) = 0\). \(\left( 1 \right)\)
+) \( - 9 + 3 - 20 + 26 = 0\) chứng tỏ \(M \in \left( P \right)\).\(\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\), suy ra \(d \subset \left( P \right)\).
Trong không gian với hệ tọa độ \(Oxyz,\) cho đường thẳng \(\Delta :\dfrac{{x - 10}}{5} = \dfrac{{y - 2}}{1} = \dfrac{{z + 2}}{1}\). Xét mặt phẳng \(\left( P \right):10x + 2y + mz + 11 = 0\) với \(m\) là tham số thực.
Tìm tất cả các giá trị của \(m\) để mặt phẳng \(\left( P \right)\) vuông góc với đường thẳng \(\Delta \).
Đường thẳng \(\Delta \) có VTCP $\overrightarrow {{u_\Delta }} = \left( {5;1;1} \right)$.
Mặt phẳng \(\left( P \right)\) có VTPT $\overrightarrow {{n_P}} = \left( {10;2;m} \right)$.
Để \(\Delta \bot \left( P \right){\rm{ }} \Leftrightarrow {\rm{ }}\overrightarrow {{u_\Delta }} \parallel \overrightarrow {{n_P}} {\rm{ }} \Leftrightarrow {\rm{ }}\dfrac{{10}}{5} = \dfrac{2}{1} = \dfrac{m}{1} \Leftrightarrow m = 2.\)

