Tìm số nghiệm nguyên của bất phương trình \({\left( {\dfrac{1}{3}} \right)^{\sqrt {{x^2} - 3x - 10} }} > {\left( {\dfrac{1}{3}} \right)^{x - 2}}\)
Vì $0 < \dfrac{1}{3} < 1$ nên ta có
\(\begin{array}{l}{\left( {\dfrac{1}{3}} \right)^{\sqrt {{x^2} - 3{\rm{x}} - 10} }} > {\left( {\dfrac{1}{3}} \right)^{x - 2}} \Leftrightarrow \sqrt {{x^2} - 3{\rm{x}} - 10} < x - 2 \\ \Leftrightarrow \left\{ \begin{array}{l}{x^2} - 3{\rm{x}} - 10 < {\left( {x - 2} \right)^2}\\{x^2} - 3{\rm{x}} - 10 \ge 0\\x - 2 > 0\end{array} \right. \Leftrightarrow 5 \le x < 14\\ \Rightarrow x = \left\{ {5,6,7,8,9,10,11,12,13} \right\}\end{array}\)
Tìm tập nghiệm của bất phương trình \(0,{3^{{x^2} + x}} > 0,09\)
$0,{3^{{x^2} + x}} > 0,09 \Leftrightarrow 0,{3^{{x^2} + x}} > 0,{3^2} \Leftrightarrow {x^2} + x - 2 < 0 \Leftrightarrow - 2 < x < 1$
Cho hàm số $f\left( x \right) = \dfrac{{{3^x}}}{{{7^{{x^2} - 4}}}}$. Hỏi khẳng định nào sau đây là sai?
\(\begin{array}{l}f(x) = \dfrac{{{3^x}}}{{{7^{{x^2} - 4}}}} > 9 \Leftrightarrow {3^x} > {9.7^{{x^2} - 4}} \Leftrightarrow {3^x} > {3^2}{.7^{{x^2} - 4}} \Leftrightarrow {3^{x - 2}} > {7^{{x^2} - 4}}\\ \Leftrightarrow {\log _3}{3^{x - 2}} > {\log _3}{7^{{x^2} - 4}} \Leftrightarrow x - 2 > ({x^2} - 4){\log _3}7\end{array}\)
Từ đó dựa vào các đáp án ta thấy A đúng.
$\begin{array}{l}{3^{x - 2}} > {7^{{x^2} - 4}}\\ \Leftrightarrow \ln {3^{x - 2}} > \ln {7^{{x^2} - 4}} \Leftrightarrow (x - 2)\ln3 > ({x^2} - 4)\ln 7\end{array}$ => B đúng
$\begin{array}{l}{3^{x - 2}} > {7^{{x^2} - 4}}\\ \Leftrightarrow \log {3^{x - 2}} > \log {7^{{x^2} - 4}} \Leftrightarrow (x - 2)\log3 > ({x^2} - 4)\log 7\end{array}$ => C đúng
$\begin{array}{l}{3^{x - 2}} > {7^{{x^2} - 4}}\\ \Leftrightarrow {\log _{0,2}}{3^{x - 2}} < {\log _{0,2}}{7^{{x^2} - 4}} \Leftrightarrow (x - 2)\log_{{0,2}}3 < ({x^2} - 4){\log _{0,2}}7\end{array}$ => D sai
Có bao nhiêu giá trị thực của \(m\) để bất phương trình \({4^x} - \left( {m + 1} \right){2^x} + m < 0\) vô nghiệm?
\({4^x} - \left( {m + 1} \right){2^x} + m < 0\,\,\,\,\left( 1 \right)\)
Đặt \({2^x} = t\,\,\left( {t > 0} \right).\)
Khi đó bất phương trình đã cho \( \Leftrightarrow {t^2} - \left( {m + 1} \right)t + m < 0\,\,\,\left( * \right).\)
TH1: \(m = 1 \Rightarrow \left( * \right) \Leftrightarrow {t^2} - 2t + 1 < 0 \Leftrightarrow {\left( {t - 1} \right)^2} < 0\) \( \Rightarrow \) bất phương trình vô nghiệm.
\( \Rightarrow m = 1\) thỏa mãn.
TH2: \(m \ne 1\)
\(\begin{array}{l} \Rightarrow \left( * \right) \Leftrightarrow {t^2} - mt - t + m < 0\\ \Leftrightarrow {t^2} - t - \left( {mt - m} \right) < 0\\ \Leftrightarrow t\left( {t - 1} \right) - m\left( {t - 1} \right) < 0\\ \Leftrightarrow \left( {t - 1} \right)\left( {t - m} \right) < 0\,\,\,\end{array}\)
+) Với \(m > 1\) \( \Rightarrow \) Tập nghiệm của bất phương trình là: \(S = \left( {1;\,\,m} \right) \subset \left( {0; + \infty } \right)\)
\( \Rightarrow \) Bất phương trình \(\left( * \right)\) luôn có nghiệm \(t > 0\)
\( \Rightarrow \left( 1 \right)\) luôn có nghiệm \(x\) \( \Rightarrow m > 1\) không thỏa mãn.
+) Với \(m < 1\) \( \Rightarrow \) Tập nghiệm của bất phương trình là: \(S = \left( {m;\,\,1} \right)\)
\( \Rightarrow \) Bất phương trình \(\left( * \right)\) luôn có nghiệm \(0 < t < 1\)
\( \Rightarrow \left( 1 \right)\) luôn có nghiệm \(x\) \( \Rightarrow m < 1\) không thỏa mãn.
Vậy chỉ có \(m = 1\) thỏa mãn bài toán.
Tìm số nghiệm nguyên của bất phương trình \({\left( {\dfrac{1}{5}} \right)^{{x^2} - 2x}} \ge \dfrac{1}{{125}}\)
Ta có
${\left( {\dfrac{1}{5}} \right)^{{x^2} - 2{\rm{x}}}} \ge \dfrac{1}{{125}} \Leftrightarrow {\left( {\dfrac{1}{5}} \right)^{{x^2} - 2{\rm{x}}}} \ge {\left( {\dfrac{1}{5}} \right)^3} $
$\Leftrightarrow {x^2} - 2{\rm{x}} \le 3 \Leftrightarrow {x^2} - 2{\rm{x - 3}} \le {\rm{0}} \Leftrightarrow {\rm{ - 1}} \le {\rm{x}} \le {\rm{3}}$
Số nghiệm nguyên là $5$.
Cho hàm số $f\left( x \right) = {5^x}{.9^{{x^3}}}$, chọn phép biến đổi sai khi giải bất phương trình:
$\begin{array}{l}f\left( x \right) > 1 \Leftrightarrow {5^x}{.9^{{x^3}}} > 1 \Leftrightarrow \ln \left( {{5^x}{{.9}^{{x^3}}}} \right) > 0 \Leftrightarrow x\ln 5 + {x^3}\ln 9 > 0\\ \Leftrightarrow x.\dfrac{{\ln 5}}{{\ln 9}} + {x^3} > 0 \Leftrightarrow x{\log _9}5 + {x^3} > 0\\ \Leftrightarrow x + {x^3}.\dfrac{1}{{{{\log }_9}5}} > 0 \Leftrightarrow x + {x^3}{\log _5}9 > 0\end{array}$
Do đó B, C, D đúng
Tập nghiệm của bất phương trình \({\left( {{x^2} + x + 1} \right)^x} < 1\) là:
\({\left( {{x^2} + x + 1} \right)^x} < 1\)
Lấy loganepe hai vế ta có \(\ln {\left( {{x^2} + x + 1} \right)^x} < \ln 1\,\,\left( * \right)\)
Vì \({x^2} + x + 1 = {\left( {x + \dfrac{1}{2}} \right)^2} + \dfrac{3}{4} > 0 \Rightarrow \left( * \right) \Leftrightarrow x\ln \left( {{x^2} + x + 1} \right) < 0 \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x < 0\\\ln \left( {{x^2} + x + 1} \right) > 0\end{array} \right.\\\left\{ \begin{array}{l}x > 0\\\ln \left( {{x^2} + x + 1} \right) < 0\end{array} \right.\end{array} \right.\)
$ \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x < 0\\{x^2} + x + 1 > 1\end{array} \right.\\\left\{ \begin{array}{l}x > 0\\{x^2} + x + 1 < 1\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x < 0\\{x^2} + x > 0\end{array} \right.\\\left\{ \begin{array}{l}x > 0\\{x^2} + x < 0\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x < 0\\\left[ \begin{array}{l}x > 0\\x < - 1\end{array} \right.\end{array} \right.\\\left\{ \begin{array}{l}x > 0\\ - 1 < x < 0\end{array} \right.\end{array} \right. \Leftrightarrow x < - 1$
Vậy tập nghiệm của bất phương trình là \(\left( { - \infty ; - 1} \right)\).
Tập nghiệm của bất phương trình \({3^{\sqrt {2x} + 1}} - {3^{x + 1}} \le {x^2} - 2x\) là:
ĐK: \(x \ge 0\)
${3^{\sqrt {2x} + 1}} - {3^{x + 1}} \le {x^2} - 2x \Leftrightarrow {3^{\sqrt {2x} + 1}} + 2x \le {3^{x + 1}} + {x^2} \Leftrightarrow {3^{\sqrt {2x} + 1}} + {\left( {\sqrt {2x} } \right)^2} \le {3^{x + 1}} + {x^2}$
Xét hàm số \(f\left( t \right) = {3^{t + 1}} + {t^2}\) có \(f'\left( t \right) = {3^{t + 1}}.\ln 3 + 2t > 0\,\,\forall t \ge 0 \Rightarrow \) Hàm số đồng biến trên \(\left[ {0; + \infty } \right)\)
Mà \(f\left( {\sqrt {2x} } \right) \le f\left( x \right) \Leftrightarrow \sqrt {2x} \le x \Leftrightarrow 2x \le {x^2} \Leftrightarrow {x^2} - 2x \ge 0 \Leftrightarrow x \in \left( { - \infty ;0} \right] \cup \left[ {2; + \infty } \right)\)
Mà \(x \ge 0 \Rightarrow x \in \left[ {2; + \infty } \right) \cup \left\{ 0 \right\}\)
Số nghiệm nguyên của bất phương trình \({4^x} - {5.2^x} + 4 < 0\) là:
Ta có: \({4^x} - {5.2^x} + 4 < 0\,\,\,\left( * \right)\)
Đặt \(t = {2^x}\,\,\,\left( {t > 0} \right)\)
\(\begin{array}{l} \Rightarrow \left( * \right) \Leftrightarrow {t^2} - 5t + 4 < 0\\ \Leftrightarrow \left( {t - 1} \right)\left( {t - 4} \right) < 0\\ \Leftrightarrow 1 < t < 4\\ \Leftrightarrow 1 < {2^x} < 4\\ \Leftrightarrow 0 < x < 2\end{array}\)
Mà \(x \in \mathbb{Z}\) \( \Rightarrow x = 1.\)
Vậy bất phương trình có 1 nghiệm nguyên.
Có bao nhiêu giá trị nguyên của tham số \(m\) để bất phương trình \(\left( {{3^{{x^2} - x}} - 9} \right)\left( {{2^{{x^2}}} - m} \right) \le 0\) có 5 nghiệm nguyên?
\(\left( {{3^{{x^2} - x}} - 9} \right)\left( {{2^{{x^2}}} - m} \right) \le 0\)
TH1: \(\left\{ \begin{array}{l}{3^{{x^2} - x}} - 9 \le 0\,\,\,\,\left( 1 \right)\\{2^{{x^2}}} - m \ge 0\,\,\,\,\,\,\left( 2 \right)\end{array} \right.\,\,\,\left( I \right)\)
\(\left( 1 \right) \Leftrightarrow {3^{{x^2} - x}} \le {3^2} \Leftrightarrow {x^2} - x \le 2 \Leftrightarrow - 1 \le x \le 2\).
\( \Rightarrow \) Số nghiệm nguyên của bất phương trình (1) là 4 nghiệm, gồm \(\left\{ { - 1;0;1;2} \right\}\).
Như vậy hệ có tối đa 4 nghiệm nguyên, hay bất phương trình ban đầu cũng chỉ có tối đa 4 nghiệm nguyên (Loại).
TH2: \(\left\{ \begin{array}{l}{3^{{x^2} - x}} - 9 \ge 0\,\,\,\,\left( {1'} \right)\\{2^{{x^2}}} - m \le 0\,\,\,\,\,\,\left( {2'} \right)\end{array} \right.\,\,\,\left( {II} \right)\)
\(\left( {1'} \right) \Leftrightarrow \left[ \begin{array}{l}x \ge 2\\x \le - 1\end{array} \right.\).
\(\left( {2'} \right) \Leftrightarrow {2^{{x^2}}} \le m \Leftrightarrow {x^2} \le {\log _2}m \Leftrightarrow - \sqrt {{{\log }_2}m} \le x \le \sqrt {{{\log }_2}m} \).

Để (II) có nghiệm thì \(\left\{ \begin{array}{l} - \sqrt {{{\log }_2}m} \le - 1\\\sqrt {{{\log }_2}m} \ge 2\end{array} \right.\).
Mà bất phương trình ban đầu có 5 nghiệm nguyên nên các nghiệm đó bắt buộc phải là -3, -2, -1, 2, 3.
Do đó
\(\begin{array}{l} 3 \le \sqrt {{{\log }_2}m} < 4\\ \Leftrightarrow 9 \le {\log _2}m < 16\\ \Leftrightarrow 512 \le m < 65536\end{array}\)
Vậy có \(65535 - 512 + 1 = 65024\) giá trị nguyên của \(m\) thỏa mãn yêu cầu bài toán.
Gọi \(S\) là tập hợp các số tự nhiên \(n\) có 4 chữ số thỏa mãn \({\left( {{2^n} + {3^n}} \right)^{2020}} < {\left( {{2^{2020}} + {3^{2020}}} \right)^n}\). Số phần tử của \(S\) là:
\(\begin{array}{l}\,\,\,\,\,\,{\left( {{2^n} + {3^n}} \right)^{2020}} < {\left( {{2^{2020}} + {3^{2020}}} \right)^n}\\ \Leftrightarrow \ln {\left( {{2^n} + {3^n}} \right)^{2020}} < \ln {\left( {{2^{2020}} + {3^{2020}}} \right)^n}\\ \Leftrightarrow 2020\ln \left( {{2^n} + {3^n}} \right) < n\ln \left( {{2^{2020}} + {3^{2020}}} \right)\\ \Leftrightarrow \dfrac{{\ln \left( {{2^n} + {3^n}} \right)}}{n} < \dfrac{{\ln \left( {{2^{2020}} + {3^{2020}}} \right)}}{{2020}}\end{array}\)
Xét hàm đặc trưng \(f\left( x \right) = \dfrac{{\ln \left( {{2^x} + {3^x}} \right)}}{x}\,\,\left( {x \in {\mathbb{N}^*}} \right)\) ta có:
\(\begin{array}{l}f'\left( x \right) = \dfrac{{\dfrac{{\left( {{2^x} + {3^x}} \right)'}}{{{2^x} + {3^x}}}.x - \ln \left( {{2^x} + {3^x}} \right)}}{{{x^2}}}\,\,\forall x \in {\mathbb{N}^*}\\f'\left( x \right) = \dfrac{{\left( {{2^x}\ln 2 + {3^x}\ln 3} \right)x - \left( {{2^x} + {3^x}} \right).\ln \left( {{2^x} + {3^x}} \right)}}{{{x^2}\left( {{2^x} + {3^x}} \right)}}\,\,\forall x \in {\mathbb{N}^*}\\f'\left( x \right) = \dfrac{{{2^x}\ln 2.x - {2^x}\ln \left( {{2^x} + {3^x}} \right) + {3^x}\ln 3.x - {3^x}\ln \left( {{2^x} + {3^x}} \right)}}{{{x^2}\left( {{2^x} + {3^x}} \right)}}\,\,\forall x \in {\mathbb{N}^*}\\f'\left( x \right) = \dfrac{{{2^x}\left( {x\ln 2 - \ln \left( {{2^x} + {3^x}} \right)} \right) + {3^x}\left( {x\ln 3 - \ln \left( {{2^x} + {3^x}} \right)} \right)}}{{{x^2}\left( {{2^x} + {3^x}} \right)}}\,\,\forall x \in {\mathbb{N}^*}\\f'\left( x \right) = \dfrac{{{2^x}\left[ {\ln {2^x} - \ln \left( {{2^x} + {3^x}} \right)} \right] + {3^x}\left[ {\ln {3^x} - \ln \left( {{2^x} + {3^x}} \right)} \right]}}{{{x^2}\left( {{2^x} + {3^x}} \right)}}\,\,\forall x \in {\mathbb{N}^*}\end{array}\)
Vì \(\left\{ \begin{array}{l}{2^x} < {2^x} + {3^x} \Rightarrow \ln {2^x} < \ln \left( {{2^x} + {3^x}} \right)\\{3^x} < {2^x} + {3^x} \Rightarrow \ln {3^x} < \ln \left( {{2^x} + {3^x}} \right)\end{array} \right.\) \( \Rightarrow f'\left( x \right) < 0\,\,\forall x \in {\mathbb{N}^*}\).
\( \Rightarrow \) Hàm số \(y = f\left( x \right)\) nghịch biến trên \({\mathbb{N}^*}\).
Lại có: \(f\left( n \right) < f\left( {2020} \right) \Leftrightarrow n > 2020\).
Kết hợp điều kiện đề bài ta có \(2020 < n \le 9999,\,\,n \in {\mathbb{N}^*}\).
Vậy có \(\dfrac{{9999 - 2021}}{1} + 1 = 7979\) giá trị của \(n\) thỏa mãn yêu cầu bài toán.
Cho \(x;y\) là hai số thực dương thỏa mãn \(x \ne y\) và \({\left( {{2^x} + \dfrac{1}{{{2^x}}}} \right)^y} < {\left( {{2^y} + \dfrac{1}{{{2^y}}}} \right)^x}.\) Tìm giá trị nhỏ nhất của biểu thức \(P = \dfrac{{{x^2} + 3{y^2}}}{{xy - {y^2}}}\).
Ta có
\(\begin{array}{l}P = \dfrac{{{x^2} + 3{y^2}}}{{xy - {y^2}}}\\ \Leftrightarrow Pxy - P{y^2} = {x^2} + 3{y^2}\\ \Leftrightarrow \left( {P + 3} \right){y^2} - Pxy + {x^2} = 0\end{array}\)
Phương trình trên có nghiệm khi
\(\begin{array}{l}\Delta = {P^2}{x^2} - 4\left( {P + 3} \right){x^2} \ge 0\\ \Leftrightarrow {P^2} - 4P - 12 \ge 0\\ \Rightarrow \left[ \begin{array}{l}P \ge 6\\P \le - 2\end{array} \right. \Rightarrow MinP = 6\end{array}\)
Dấu bằng xáy ra khi \(\left\{ \begin{array}{l}y = \dfrac{{Px}}{{2\left( {P + 3} \right)}} = \dfrac{x}{3}\\\dfrac{{{x^2} + 3{y^2}}}{{xy - {y^2}}} = 6\end{array} \right. \Rightarrow x = 3y\)
Dễ thấy \(x=3y\) thỏa mãn điều kiện bài cho vì:
$\begin{array}{l}
{\left( {{2^{3y}} + \frac{1}{{{2^{3y}}}}} \right)^y} < {\left( {{2^y} + \frac{1}{{{2^y}}}} \right)^{3y}}\\
\Leftrightarrow {2^{3y}} + \frac{1}{{{2^{3y}}}} < {\left( {{2^y} + \frac{1}{{{2^y}}}} \right)^3}\\
\Leftrightarrow {2^{3y}} + \frac{1}{{{2^{3y}}}} < {2^{3y}} + \frac{1}{{{2^{3y}}}} + {3.2^y}.\frac{1}{{{2^y}}}.\left( {{2^y} + \frac{1}{{{2^y}}}} \right)\\
\Leftrightarrow 0 < 3\left( {{2^y} + \frac{1}{{{2^y}}}} \right)
\end{array}$
Bđt trên luôn đúng với mọi \(y>0\).
Cho hàm số \(y = f\left( x \right)\). Hàm số \(y = f'\left( x \right)\) có bảng biến thiên như sau:
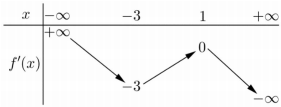
Bất phương trình \(f\left( x \right) < {e^x} + m\) đúng với mọi \(x \in \left( { - 1;1} \right)\) khi và chỉ khi:
Theo đề bài ta có : \(f\left( x \right) < {e^x} + m \Leftrightarrow f\left( x \right) - {e^x} < m\)
Đặt \(g\left( x \right) = f\left( x \right) - {e^x}.\) Khi đó :
\(\begin{array}{l}f\left( x \right) < {e^x} + m\,\,\forall x \in \left( { - 1;1} \right)\\ \Rightarrow g\left( x \right) = f\left( x \right) - {e^x} < m\,\,\forall x \in \left( { - 1;1} \right)\\ \Leftrightarrow m \ge \mathop {\max }\limits_{\left[ { - 1;1} \right]} g\left( x \right)\\g'\left( x \right) = f'\left( x \right) - {e^x}\end{array}\)
Trên \(\left( { - 1;1} \right)\) ta có \(f'\left( x \right) < 0;\,\,{e^x} > 0\,\,\forall x \in R \Rightarrow g'\left( x \right) < 0\,\,\forall x \in \left( { - 1;1} \right)\)
\( \Rightarrow g\left( x \right)\) nghịch biến trên \(\left( { - 1;\;1} \right).\)
\(\begin{array}{l} \Rightarrow \mathop {\max }\limits_{\left[ { - 1;1} \right]} g\left( x \right) = g\left( { - 1} \right) = f\left( { - 1} \right) - {e^{ - 1}} = f\left( { - 1} \right) - \dfrac{1}{e}\\ \Rightarrow m \ge f\left( { - 1} \right) - \dfrac{1}{e}.\end{array}\)
Đề thi THPT QG 2020 – mã đề 104
Xét các số thực không âm \(x\) và \(y\) thỏa mãn \(2x + y{.4^{x + y - 1}} \ge 3\). Giá trị nhỏ nhất của biểu thức \(P = {x^2} + {y^2} + 4x + 2y\) bằng
Ta có: \(2x + y{.4^{x + y - 1}} \ge 3\)
\(\begin{array}{l} \Leftrightarrow 2x - 3 + y{.4^x}{.4^{y - 1}} \ge 0\\ \Leftrightarrow \left( {2x - 3} \right){.4^{ - x}} + y{.4^{y - 1}} \ge 0\\ \Leftrightarrow y{.4^{y - 1}} \ge \left( {3 - 2x} \right){.4^{ - x}}\\ \Leftrightarrow y{.2^{2y - 2}} \ge \left( {3 - 2x} \right){.2^{ - 2x}}\\ \Leftrightarrow {2^3}.y{.2^{2y - 2}} \ge {2^3}.\left( {3 - 2x} \right){.2^{ - 2x}}\\ \Leftrightarrow 2y{.2^{2y}} \ge \left( {3 - 2x} \right){.2^{3 - 2x}}\,\,\,\,\left( 1 \right)\end{array}\)
TH1: Với \(3 - 2x \le 0\) \( \Leftrightarrow x \ge \dfrac{3}{2}\)
\( \Rightarrow \left( 1 \right)\) đúng với mọi giá trị \(\left\{ \begin{array}{l}x \ge \dfrac{3}{2}\\y \ge 0\end{array} \right.\)
\( \Rightarrow P = {x^2} + {y^2} + 4x + 2y \ge \dfrac{{33}}{4}\,\,\,\left( 2 \right)\)
TH2: Với \(3 - 2x > 0\) \( \Leftrightarrow 0 \le x < \dfrac{3}{2}\)
Xét hàm số: \(f\left( t \right) = t{.2^t}\) với \(t \ge 0\)
\( \Rightarrow f'\left( t \right) = {2^t} + t{.2^t}.\ln 2 > 0\,\,\forall t \ge 0\)
\( \Rightarrow f\left( t \right)\) là hàm số đồng biến trên \(\left( {0; + \infty } \right).\)
\(\begin{array}{l} \Rightarrow \left( 1 \right) \Leftrightarrow f\left( {2y} \right) \ge f\left( {3 - 2x} \right)\\ \Leftrightarrow 2y \ge 3 - 2x\\ \Leftrightarrow y \ge \dfrac{3}{2} - x\end{array}\)
\( \Rightarrow P = {x^2} + {y^2} + 4x + 2y\)\( \ge {x^2} + {\left( {\dfrac{3}{2} - x} \right)^2} + 4x + 3 - 2x\) \( = 2{x^2} - x + \dfrac{{21}}{4}\)
\( \Rightarrow P = 2{\left( {x - \dfrac{1}{4}} \right)^2} + \dfrac{{41}}{8} \ge \dfrac{{41}}{8}\,\,\,\left( 3 \right)\)
Từ (2) và (3) ta được: \(Min\,\,P = \dfrac{{41}}{8}\)
Dấu “=” xảy ra \( \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{1}{4}\\y = \dfrac{5}{4}\end{array} \right..\)

