Số nghiệm thực của phương trình $({z^2} + 1)({z^2} - i) = 0$ là
Có ${z^2} + 1 \ne 0,\forall z \in R$ và ${z^2}-i \ne 0,\forall z \in R$.
Vậy phương trình đã cho không có nghiệm thực.
Kí hiệu ${z_1},{z_2},{z_3},{z_4}$ là bốn nghiệm phức của phương trình ${z^4} - {z^2} - 12 = 0$. Tính tổng $T = \left| {{z_1}} \right| + \left| {{z_2}} \right| + \left| {{z_3}} \right| + \left| {{z_4}} \right|$.
$\begin{array}{l}{z^4} - {z^2} - 12 = 0 \Leftrightarrow \left( {{z^2} - 4} \right)\left( {{z^2} + 3} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}z = \pm 2\\z = \pm i\sqrt 3 \end{array} \right.\\ \Rightarrow T = 2 + 2 + \sqrt 3 + \sqrt 3 = 4 + 2\sqrt 3 \end{array}$
Tổng \(S = C_{2019}^0 + C_{2019}^3 + C_{2019}^6 + ... + C_{2019}^{2019}\) bằng
+ Ta tìm các số phức \(z\) thỏa mãn \({z^3} = 1\). Ta có \({z^3} = 1 \Leftrightarrow {z^3} - 1 = 0 \Leftrightarrow \left( {z - 1} \right)\left( {{z^2} + z + 1} \right) = 0\)
\( \Leftrightarrow \left[ \begin{array}{l}z = 1\\{z^2} + z + 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}{z_1} = 1\\{z_2} = - \dfrac{1}{2} + \dfrac{{\sqrt 3 }}{2}i\\{z_3} = - \dfrac{1}{2} - \dfrac{{\sqrt 3 }}{2}i\end{array} \right.\)
+ Xét khai triển
\({\left( {1 + x} \right)^{2019}} = \sum\limits_{k = 0}^{2019} {C_{2019}^k{x^k} = C_{2019}^0 + C_{2019}^1x + C_{2019}^2{x^2} + C_{2019}^3{x^3} + C_{2019}^4{x^4} + C_{2019}^5{x^5} + C_{2019}^6{x^6} + ... + C_{2019}^{2019}{x^{2019}}} \) (*)
+ Thay \({z_2} = - \dfrac{1}{2} + \dfrac{{\sqrt 3 }}{2}i\) vào khai triển (*) ta được
\(\begin{array}{l}{\left( {1 - \dfrac{1}{2} + \dfrac{{\sqrt 3 }}{2}i} \right)^{2019}} \\= C_{2019}^0 + C_{2019}^1{z_2} + C_{2019}^2{z_2}^2 + C_{2019}^3{z_2}^3 \\+ C_{2019}^4{z_2}^4 + C_{2019}^5{z_2}^5 + C_{2019}^6{z_2}^6 + ... + C_{2019}^{2019}{z_2}^{2019}\\ \Leftrightarrow {\left( {\dfrac{1}{2} + \dfrac{{\sqrt 3 }}{2}i} \right)^{2019}} = C_{2019}^0 + C_{2019}^1{z_2} + C_{2019}^2{z_2}^2\\ + C_{2019}^3 + C_{2019}^4{z_2} + C_{2019}^5{z_2}^2 + C_{2019}^6 + ... + C_{2019}^{2019}\\ \Leftrightarrow - 1 = \left( {C_{2019}^0 + C_{2019}^3 + C_{2019}^6 + ... + C_{2019}^{2019}} \right) + {z_2}\left( {C_{2019}^1 + C_{2019}^4 + ... + C_{2019}^{2017}} \right) + z_2^2\left( {C_{2019}^2 + C_{2019}^5 + ... + C_{2019}^{2018}} \right)\,\left( 1 \right)\end{array}\)
+ Tương tự thay \({z_3} = - \dfrac{1}{2} - \dfrac{{\sqrt 3 }}{2}i\) vào khai triển (*) ta được
\(\begin{array}{l}{\left( {1 - \dfrac{1}{2} - \dfrac{{\sqrt 3 }}{2}i} \right)^{2019}} = C_{2019}^0 + C_{2019}^1{z_3} + C_{2019}^2{z_3}^2 \\+ C_{2019}^3{z_3}^3 + C_{2019}^4{z_3}^4 + C_{2019}^5{z_3}^5 + C_{2019}^6{z_3}^6 + ... + C_{2019}^{2019}{z_3}^{2019}\\ \Leftrightarrow {\left( {\dfrac{1}{2} - \dfrac{{\sqrt 3 }}{2}i} \right)^{2019}} = C_{2019}^0 + C_{2019}^1{z_3} + C_{2019}^2{z_3}^2\\ + C_{2019}^3 + C_{2019}^4{z_3} + C_{2019}^5{z_3}^2 + C_{2019}^6 + ... + C_{2019}^{2019}\\ \Leftrightarrow - 1 = \left( {C_{2019}^0 + C_{2019}^3 + C_{2019}^6 + ... + C_{2019}^{2019}} \right) + {z_3}\left( {C_{2019}^1 + C_{2019}^4 + ... + C_{2019}^{2017}} \right) + z_3^2\left( {C_{2019}^2 + C_{2019}^5 + ... + C_{2019}^{2018}} \right)\left( 2 \right)\end{array}\)
+ Thay \(z = 1\) vào vào khai triển (*) ta được
\(\begin{array}{l}{2^{2019}} = C_{2019}^0 + C_{2019}^1 + C_{2019}^2 + C_{2019}^3 + C_{2019}^4 + C_{2019}^5 + C_{2019}^6 + ... + C_{2019}^{2019}\\ \Leftrightarrow {2^{2019}} = \left( {C_{2019}^0 + C_{2019}^3 + C_{2019}^6 + ... + C_{2019}^{2019}} \right) + \left( {C_{2019}^1 + C_{2019}^4 + C_{2019}^7 + ... + C_{2019}^{2017}} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \left( {C_{2019}^2 + C_{2019}^5 + C_{2019}^8 + ... + C_{2019}^{2018}} \right)\left( 3 \right)\end{array}\)
Cộng vế với vế của (1) (2) và (3) ta được
\(\begin{array}{l}{2^{2019}} - 2 = 3\left( {C_{2019}^0 + C_{2019}^3 + C_{2019}^6 + ... + C_{2019}^{2019}} \right) + \left( {1 + {z_2} + {z_3}} \right)\left( {C_{2019}^1 + C_{2019}^4 + C_{2019}^7 + ... + C_{2019}^{2018}} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \left( {1 + z_2^2 + z_3^2} \right)\left( {C_{2019}^2 + C_{2019}^5 + C_{2019}^8 + ... + C_{2019}^{2017}} \right)\end{array}\)
Nhận thấy \(1 + {z_2} + {z_3} = 1 - \dfrac{1}{2} + \dfrac{{\sqrt 3 }}{2}i - \dfrac{1}{2} - \dfrac{{\sqrt 3 }}{2}i = 0\) và \(1 + z_2^2 + z_3^2 = 1 + {\left( { - \dfrac{1}{2} + \dfrac{{\sqrt 3 }}{2}i} \right)^2} + {\left( { - \dfrac{1}{2} - \dfrac{{\sqrt 3 }}{2}i} \right)^2} = 0\)
Nên \({2^{2019}} - 2 = 3S \Leftrightarrow S = \dfrac{{{2^{2019}} - 2}}{3}\)
Có bao nhiêu giá trị nguyên của hàm số \(m\) để phương trình \({z^2} - 2mz + 6m - 5 = 0\) có hai nghiệm phức phân biệt \({z_1},\,\,{z_2}\) thỏa mãn \(\left| {{z_1}} \right| = \left| {{z_2}} \right|?\)
Để phương trình có 2 nghiệm phức phân biệt thì \(\Delta ' < 0\) \( \Leftrightarrow {m^2} - 6m + 5 < 0 \Leftrightarrow 1 < m < 5\)
Phương trình bậc hai có 2 nghiệm phức phân biệt thì hai số phức đó là hai số phức liên hợp nên luôn thỏa mãn điều kiện \(\left| {{z_1}} \right| = \left| {{z_2}} \right|\).
\( \Rightarrow m \in \left( {1;5} \right)\). Mà \(m \in \mathbb{Z} \Rightarrow m \in \left\{ {2;3;4} \right\}\). Vậy có 3 giá trị của \(m\) thỏa mãn yêu cầu bài toán.
Biết phương trình \(2{z^2} + 4z + 3 = 0\) có hai nghiệm phức \({z_1},\,\,{z_2}\). Giá trị của \(\left| {{z_1}{z_2} + i\left( {{z_1} + {z_2}} \right)} \right|\) bằng:
Phương trình \(2{z^2} + 4z + 3 = 0\) có hai nghiệm phức \({z_1},\,\,{z_2}\) nên ta có: \(\left\{ \begin{array}{l}{z_1} + {z_2} = - 2\\{z_1}{z_2} = \dfrac{3}{2}\end{array} \right.\).
Khi đó ta có: \(\left| {{z_1}{z_2} + i\left( {{z_1} + {z_2}} \right)} \right|\)\( \Leftrightarrow \left| { - \dfrac{3}{2} + i.\left( { - 2} \right)} \right| = \sqrt {{{\left( { - \dfrac{3}{2}} \right)}^2} + {{\left( { - 2} \right)}^2}} = \dfrac{5}{2}\)
Biết phương trình \({z^2} + 2z + m = 0\,\,\left( {m \in \mathbb{R}} \right)\) có một nghiệm là \({z_1} = - 1 + 3i\). Gọi \({z_2}\) là nghiệm còn lại. Phần ảo của số phức \({\rm{w}} = {z_1} - 2{z_2}\) bằng
Phương trình \({z^2} + 2z + m = 0\) có một nghiệm \({z_1} = - 1 + 3i \Rightarrow \) Nghiệm còn lại là \({z_2} = - 1 - 3i.\)
Khi đó ta có: \(w = {z_1} - 2{z_2} = - 1 + 3i - 2\left( { - 1 - 3i} \right) = 1 + 9i\)
Vậy số phức \(w\) có phần ảo bằng 9.
Đề thi THPT QG - 2021 - mã 101
Trên tập hợp các số phức, xét phương trình \({z^2} - 2\left( {m + 1} \right)z + {m^2} = 0\) (\(m\) là tham số thực). Có bao nhiêu giá trị của \(m\) để phương trình đó có nghiệm \({z_0}\) thỏa mãn \(\left| {{z_0}} \right| = 7\)?
Đặt \({z^2} - 2\left( {m + 1} \right)z + {m^2} = 0\) (*).
TH1: \({z_0}\) là nghiệm thực \( \Rightarrow \left| {{z_0}} \right| = 7 \Leftrightarrow \left[ \begin{array}{l}{z_0} = 7\\{z_0} = - 7\end{array} \right.\).
+ Nếu \({z_0} = 7\) thay vào (*)
\(\begin{array}{l} \Rightarrow {7^2} - 14\left( {m + 1} \right) + {m^2} = 0\\ \Leftrightarrow {m^2} - 14m + 35 = 0\\ \Leftrightarrow m = 7 \pm \sqrt {14} \end{array}\)
\( \Rightarrow \) Có 2 giá trị thỏa mãn \(m = 7 \pm \sqrt {14} \) thì phương trình (*) có nghiệm \({z_0} = 7\) (tmycbt).
+ Nếu \({z_0} = - 7\) thay vào (*)
\(\begin{array}{l} \Rightarrow 49 + 14\left( {m + 1} \right) + {m^2} = 0\\ \Leftrightarrow {m^2} + 14m + 63 = 0\end{array}\)
\( \Rightarrow \) Vô nghiệm.
TH2: \({z_0}\) là nghiệm có chứa \(i \Leftrightarrow \Delta ' = {\left( {m + 1} \right)^2} - {m^2} < 0 \Leftrightarrow 2m + 1 < 0 \Leftrightarrow m < - \dfrac{1}{2}\).
Theo tính chất của phương trình bậc hai trên tập phức, nếu phương trình (*) có 1 nghiệm phức \({z_0}\) chứa \(i\) thì sẽ có 1 nghiệm phức còn lại là \(\overline {{z_0}} \).
Điều kiện \(\left| {{z_0}} \right| = 7 \Leftrightarrow {\left| {{z_0}} \right|^2} = 7 \Leftrightarrow {z_0}.\overline {{z_0}} = {7^2} \Leftrightarrow {z_0}.\overline {{z_0}} = 49\,\,\left( 1 \right)\).
Vì \({z_0}\) và \(\overline {{z_0}} \) là 2 nghiệm của phương trình (*), theo định lí Vi-ét ta có: \({z_0}.\overline {{z_0}} = {m^2}\,\,\,\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow {m^2} = 49 \Leftrightarrow m = \pm 7\).
So sánh điều kiện \(m < - \dfrac{1}{2} \Rightarrow m = - 7\).
Vậy tất cả TH1 và TH2 có 3 giá trị của \(m\) thỏa mãn yêu cầu bài toán (\(m = 7 \pm \sqrt {14} \) và \(m = - 7\)).
Số nghiệm phức của phương trình \({z^2} + \left| z \right| = 0\) là:
Bước 1:
Ta có: \({z^2} + \left| z \right| = 0 \Leftrightarrow \left| z \right| = - {z^2}\).
Bước 2:
Lấy môđun 2 vế của phương trình ta có:
\({\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left| {\left| z \right|} \right| = \left| { - {z^2}} \right| \Leftrightarrow \left| z \right| = {\left| z \right|^2}\)
\( \Leftrightarrow \left| z \right|\left( {1 - \left| z \right|} \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{\left| z \right| = 0}\\{\left| z \right| = 1{\mkern 1mu} {\mkern 1mu} }\end{array}} \right.\)
Bước 3:
\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{z = 0}\\{{z^2} + 1 = 0}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{z = 0}\\{z = {\rm{\;}} \pm i}\end{array}} \right.\)
Vậy phương trình đã cho có 3 nghiệm phức duy nhất \(z = 0,\,\,z = \pm i\).
Gọi $S$ là tổng các giá trị thực của $m$ để phương trình $9 z^{2}+6 z+1-m=0$ có nghiệm phức thỏa mãn $|z|=1$. Tính $S$
12
12
12
Bước 1: Tính $\Delta^{\prime}$
Phương trình $9 z^{2}+6 z+1-m=0(*)$ có $\Delta^{\prime}=9-9(1-m)=9 m$
Xét hai trường hợp sau:
Bước 2: Trường hợp (*) có nghiệm thực
Trường hợp 1. (*) có nghiệm thực $\Leftrightarrow \Delta^{\prime} \geq 0 \Leftrightarrow m \geq 0$
Khi đó, $|z|=1 \Leftrightarrow\left[\begin{array}{l}z=1 \\ z=-1\end{array}\right.$
$+) z=1 \Rightarrow m=16$ (thỏa mãn)
$+) z=-1 \Rightarrow m=4$ (thỏa mãn)
Bước 3: Trường hợp (*) có nghiệm phức
Trường hợp 2. (*) có nghiệm phức $z=a+b i(b \neq 0) \Leftrightarrow \Delta^{\prime}<0 \Leftrightarrow m<0$
Nếu $z$ là một nghiệm của phương trình $9 z^{2}+6 z+1-m=0$ thì $\bar{z}$ cũng là một nghiệm của phương trình $9 z^{2}+6 z+1-m=0$
Ta có $|z|=1 \Leftrightarrow|z|^{2}=1 \Leftrightarrow z . \bar{z}=1 \Leftrightarrow \dfrac{1-m}{9}=1 \Leftrightarrow m=-8$ (thỏa mãn)
Vậy tổng các giá trị thực của $m$ bằng $16+4+(-8)=12$.
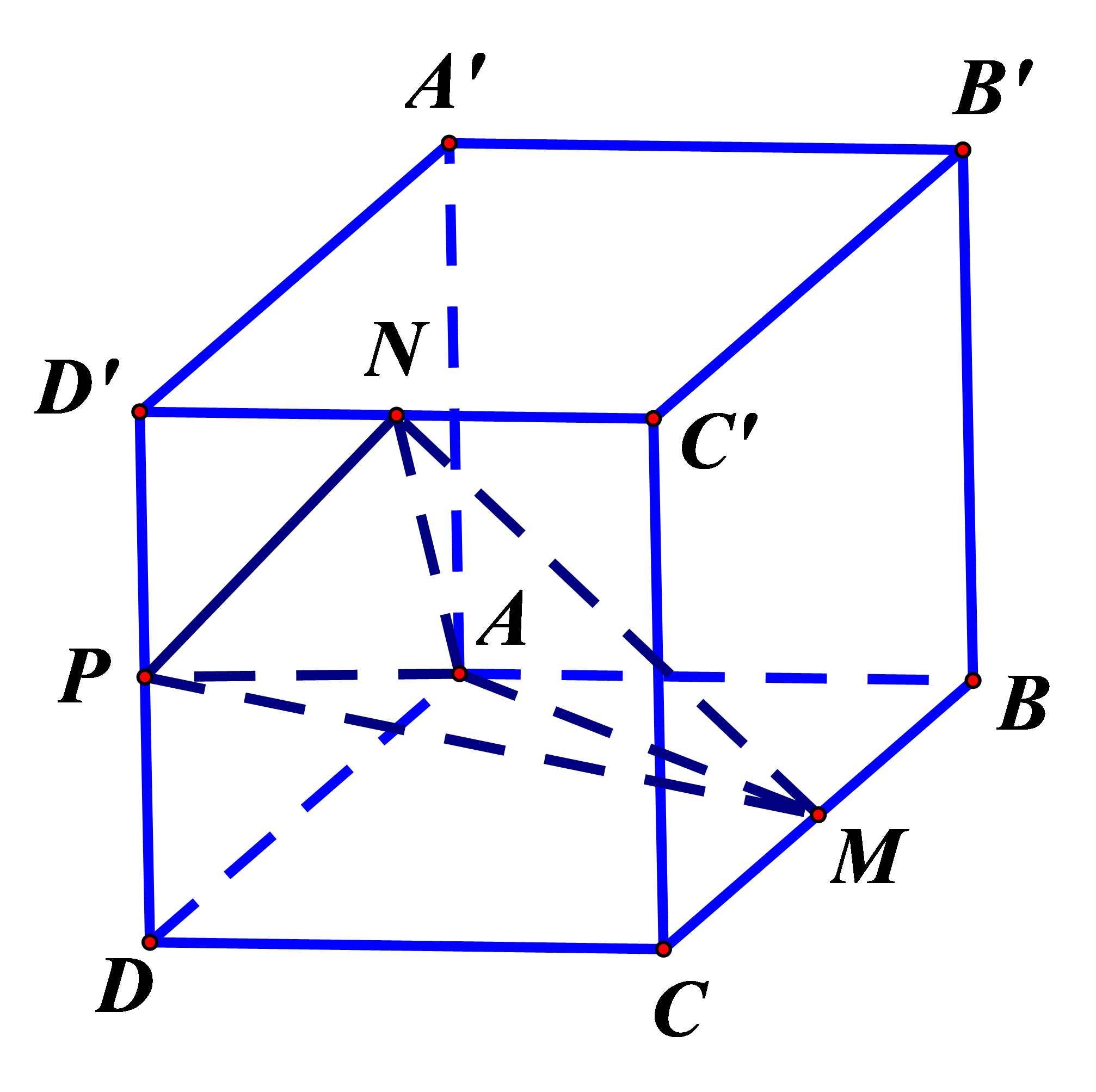
Cho hình hộp chữ nhật $A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ có $M, N, P$ lần lượt là trung điểm các cạnh $B C, C^{\prime} D^{\prime}, D D^{\prime}$ (tham khảo hình vẽ). Biết thể tích khối hộp bằng 144 , thể tích khối tứ diện $A M N P$ bằng
15
15
15
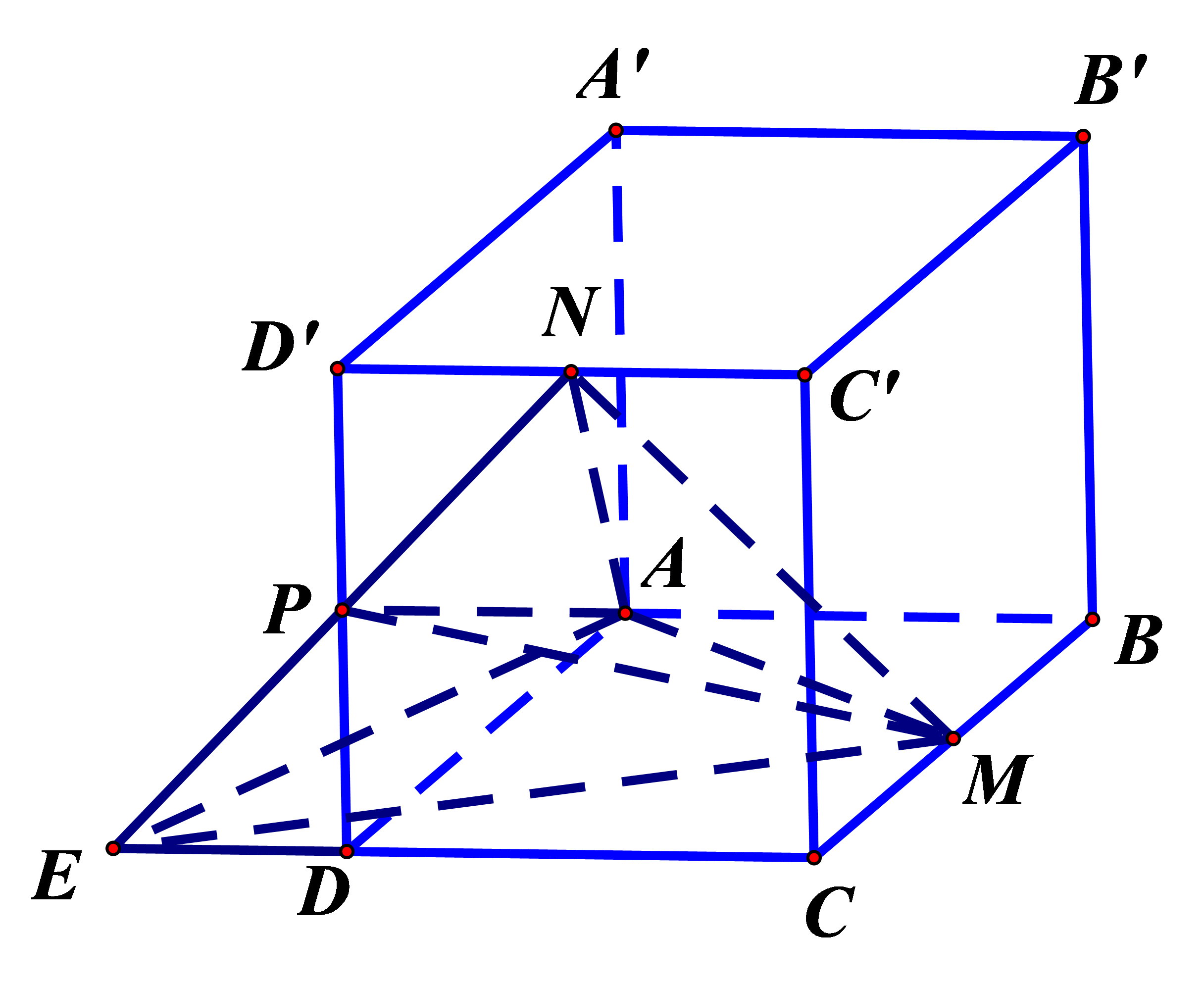
Bước 1: Gọi $E=N P \cap C D$. Đặt $D C=2 d, B C=2 r$
Gọi $E=N P \cap C D$. Đặt $D C=2 d, B C=2 r$
Ta có:
\(\begin{array}{l}{S_{EMA}} = {S_{ECBA}} - {S_{EMC}} - {S_{ABM}}\\ = 5dr - \dfrac{3}{2}dr - dr = \dfrac{5}{2}dr\end{array}\)
Bước 2: Tính thể tích của NPAM
\(\begin{array}{l}{V_{NEAM}} = \dfrac{1}{3}{S_{EMA}} \cdot d(N,(EMA))\\ = \dfrac{1}{3}{S_{EMA}} \cdot CC' = \dfrac{5}{{24}} \cdot 4dr \cdot C{C^\prime }\\ = \dfrac{5}{{24}}{V_{ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }}} = 30.\\ \Rightarrow {V_{NPAM}} = \dfrac{1}{2}{V_{NEAM}} = 15\end{array}\)
Các nghiệm của phương trình \({z^2} - z + 2 = 0\) được biểu diễn hình học bởi điểm A và điểm B trên mặt phẳng tọa độ. Độ dài của AB là
Bước 1: Tìm A và B
\({z^2} - z + 2 = 0 \Leftrightarrow \left[ \begin{array}{l}z = \dfrac{1}{2} + \dfrac{{\sqrt 7 }}{2}i\\z = \dfrac{1}{2} - \dfrac{{\sqrt 7 }}{2}i\end{array} \right.\)
Chọn \(A\left( {\dfrac{1}{2};\dfrac{{\sqrt 7 }}{2}} \right);B\left( {\dfrac{1}{2}; - \dfrac{{\sqrt 7 }}{2}} \right)\)
Bước 2: Tính độ dài AB.
Độ dài đoạn thẳng AB là: \(\sqrt {{{\left( {\dfrac{{\sqrt 7 }}{2} + \dfrac{{\sqrt 7 }}{2}} \right)}^2}} = \sqrt 7 \)
Trên tập hợp các số phức, xét phương trình \({z^2} - 2mz + 8m - 12 = 0\) (m là tham số thực). Có bao nhiêu giá trị nguyên của \(m\) để phương trình đó có hai nghiệm phân biệt \({z_1},{z_2}\) thỏa mãn \(\left| {{z_1}} \right| = \left| {{z_2}} \right|?\)
Ta có \({\Delta ^\prime } = {m^2} - 8m + 12\)
Nếu \({\Delta ^\prime } > 0\) thì phương trình có hai nghiệm thực. Khi đó:
\(\left| {{z_1}} \right| = \left| {{z_2}} \right| \Leftrightarrow {z_1} = - {z_2}\) \( \Leftrightarrow {z_1} + {z_2} = 0 \Leftrightarrow m = 0\) (thỏa mãn)
Nếu \({\Delta ^\prime } < 0\), thì phương trình có hai nghiệm phức khi đó là hai số phức liên hợp nên ta luôn có \(\left| {{z_1}} \right| = \left| {{z_2}} \right|\), hay \({m^2} - 8m + 12 < 0 \Leftrightarrow 2 < m < 6\) luôn thỏa mãn.
=> \(m \in \left\{ {3;4;5} \right\}\)
Vậy có 4 giá trị nguyên của tham số thỏa mãn

