Cho các dạng đồ thị (I), (II), (III) như hình dưới đây:
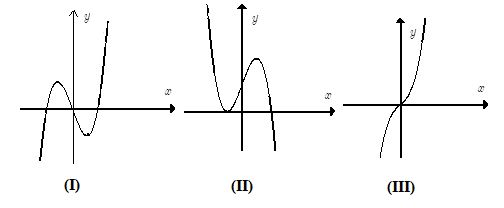
Liệt kê tất cả các dạng có thể biểu diễn đồ thị hàm số \(y = {x^3} + b{x^2} - x + d\).
Hàm số \(y = {x^3} + b{x^2} - x + d\) có hệ số của \({x^3}\) dương nên loại (II).
Xét \(y' = 3{x^2} + 2bx - 1\) có \(\Delta ' = {b^2} + 3 > 0,\forall b \in \mathbb{R}\).
Do đó hàm số có hai cực trị.
Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\) có bảng biến thiên như hình bên. Trong các hệ số a, b, c và d có bao nhiêu số âm?
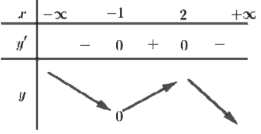
Ta có: \(\mathop {\lim }\limits_{x \to + \infty } y = - \infty \Rightarrow a < 0\).
\(y' = 3a{x^2} + 2bx + c\).
Dựa vào BBT ta thấy hàm số có hai điểm cực trị \({x_1} = - 1,\,\,{x_2} = 2\) nên phương trình \(y' = 0\) có hai nghiệm phân biệt thỏa mãn \(S = {x_1} + {x_2} = 1 > 0\), \(P = {x_1}{x_2} = - 2 < 0\) \( \Rightarrow \left\{ \begin{array}{l}\Delta ' = {b^2} - 3ac > 0\\S = \dfrac{{ - 2b}}{{3a}} > 0\\P = \dfrac{c}{{3a}} < 0\end{array} \right.\).
Mà \(a < 0\) nên \(b > 0\) và \(c > 0\).
Dựa vào BBT ta thấy tại điểm \(x = 0\) thì \(y > 0\), do đó \(d > 0\).
Vậy trong 4 hệ số a, b, c, d chỉ có 1 số âm.
Cho đồ thị (C) của hàm số \(y = {x^3} - 6{x^2} + 9x - 1\) như hình vẽ. Hãy xác định số điểm cực trị của hàm số \(y = {\left| x \right|^3} - 6{x^2} + 9\left| x \right| - 1\).
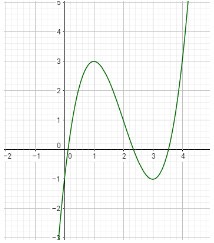
Từ đồ thị hàm số \(y = {x^3} - 6{x^2} + 9x - 1\) ta suy ra được đồ thị hàm số \(y = {\left| x \right|^3} - 6{x^2} + 9\left| x \right| - 1\) như sau (phần nét liền):
Dựa vào đồ thị hàm số ta thấy hàm số \(y = {\left| x \right|^3} - 6{x^2} + 9\left| x \right| - 1\) có 5 điểm cực trị.
Biết rằng hàm số \(y = f\left( x \right) = a{x^4} + b{x^2} + c\) có đồ thị là đường cong như hình vẽ bên dưới.
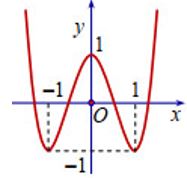
Tính giá trị \(f\left( {3a + 2b + c} \right)\).
Ta có \(f'\left( x \right) = 4a{x^3} + 2bx\).
Dựa vào đồ thị hàm số ta thấy:
Đồ thị hàm số đi qua các điểm \(\left( {0;1} \right);\,\,\left( {1; - 1} \right)\).
Đồng thời đây cũng là 2 điểm cực trị của hàm số. Do đó ta có hệ phương trình:
\(\left\{ \begin{array}{l}f\left( 0 \right) = 1\\f\left( 1 \right) = - 1\\f'\left( 1 \right) = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}c = 1\\a + b + c = - 1\\4a + 2b = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}c = 1\\a = 2\\b =- 4\end{array} \right.\).
\( \Rightarrow f\left( x \right) = 2{x^4} - 4{x^2} + 1\) và \(3a + 2b + c = 3.2 + 2.(-4) + 1 = -1\).
Vậy \(f\left( {3a + 2b + c} \right) = f\left( -1 \right) = - 1\).
Cho hàm số \(f\left( x \right) = a{x^4} + b{x^3} + c{x^2} + dx + e,\) với \(a,b,c,d,e \in \mathbb{R}.\) Hàm số \(y = f'\left( x \right)\) có đồ thị như hình vẽ. Trong các khẳng định sau, khẳng định nào đúng?
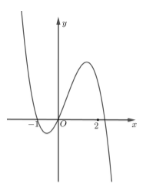
Ta có \(f'\left( x \right) = 4a{x^3} + 3b{x^2} + 2cx + d\)
Từ đồ thị hàm số ta thấy \(f'\left( 0 \right) \Leftrightarrow d = 0\)
Từ đồ thị ta thấy:
+ Khi $x< -1$ thì $f'(x)>0$.
+ Khi $-1<x<0=>f'(x)<0$
+ Khi $0<x<x_0$ (với $x_0$ là nghiệm thứ 3 của phương trình $f'(x)=0$) $=>f'(x)>0$
+ Khi $x>x_0$ thì $f'(x)<0$
Ta có bảng biến thiên:
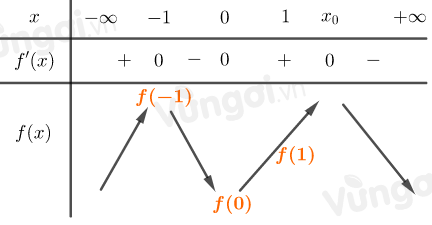
\(\Rightarrow f\left( { - 1} \right) > f\left( 0 \right)\)
\( \Leftrightarrow a - b + c - d + e > e \Leftrightarrow a + c > b + d\) nên B sai, lại có \(d = 0 \Rightarrow a + c > b\) (1)
+) Từ bảng biến thiên \( \Rightarrow f\left( 1 \right) > f\left( 0 \right)\)
\( \Leftrightarrow a + b + c + d + e > e \Leftrightarrow a + b + c + d > 0\) nên A sai.
Mà \(d = 0\) nên \(a + b + c > 0 \Leftrightarrow a + c > - b\) (2)
Từ (1) và (2) suy ra \(2\left( {a + c} \right) > 0 \Leftrightarrow a + c > 0.\)
Cho hàm số $y = f(x)$ liên tục và có đạo hàm cấp hai trên $R$. Đồ thị của các hàm số $y = f(x),y = f'(x),y = f''(x)$ lần lượt là các đường cong nào trong hình vẽ bên.
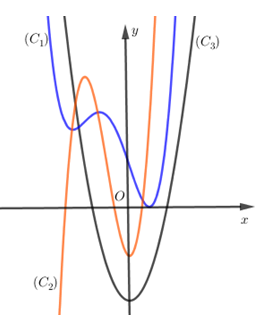
Từ đồ thị ta thấy $(C_1)$ là đồ thị của hàm bậc bốn; $(C_2)$ là đồ thị của hàm bậc ba; $\left( {{C_3}} \right)$là đồ thị hàm bậc hai (parabol) nên $(C_1)$ là đồ thị của $f(x)$; $\left( {{C_2}} \right)$ là đồ thị của $f'\left( x \right)$; $\left( {{C_3}} \right)$ là đồ thị của $f''\left( x \right)$

