Đồ thị của hàm số \(y = f\left( x \right)\) đối xứng với đồ thị của hàm số \(y = {a^x}\,\,\left( {a > 0,\,\,a \ne 1} \right)\) qua điểm \(M\left( {1;1} \right)\). Giá trị của hàm số \(y = f\left( x \right)\) tại \(x = 2 + {\log _a}\dfrac{1}{{2020}}\) bằng:
Lấy điểm \(A\left( {{x_0};{a^{{x_0}}}} \right) \in \left( {{C_1}} \right)\) (đồ thị của hàm số \(y = {a^x}\). Gọi B là điểm đối xứng của A qua M(1;1).
\( \Rightarrow \left\{ \begin{array}{l}{x_B} = 2{x_M} - {x_A} = 2 - {x_0}\\{y_B} = 2{y_M} - {y_A} = 2 - {a^{{x_0}}}\end{array} \right.\)\( \Rightarrow {x_0} = 2 - {x_B} \Rightarrow {y_B} = 2 - {a^{2 - {x_B}}}\)
\( \Rightarrow \) Hàm số \(y = f\left( x \right) = 2 - {a^{2 - x}}\)
\( \Rightarrow f\left( {2 + {{\log }_a}\dfrac{1}{{2020}}} \right) = 2 - {a^{2 - \left( {2 + {{\log }_a}\dfrac{1}{{2020}}} \right)}}\)\( = 2 - {a^{{{\log }_a}20220}} = 2 - 2020 = - 2018\).
Cho \(a\) và \(b\) là các số thực dương khác 1. Biết rằng bất kì đường thẳng nào song song với trục tung mà cắt các đồ thị \(y = {\log _a}x,\,\,y = {\log _b}x\) và trục hoành lần lượt tại \(A,\,\,B\) và \(H\) phân biệt ta đều có \(3HA = 4HB\) (hình vẽ bên dưới). Khẳng định nào sau đây là đúng?
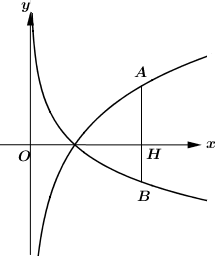
Gọi \(H\left( {{x_0};0} \right)\,\,\left( {{x_0} > 1} \right)\) ta có: \(A\left( {{x_0};{{\log }_a}{x_0}} \right);\,\,B\left( {{x_0};{{\log }_b}{x_0}} \right)\).
\( \Rightarrow HA = {\log _a}{x_0}\); \(HB = - {\log _b}{x_0}\) (do \({\log _a}{x_0} > 0,\,\,{\log _b}{x_0} < 0\)).
Theo bài ra ta có: \(3HA = 4HB\)\( \Leftrightarrow 3{\log _a}{x_0} = - 4{\log _b}{x_0}\).
\(\begin{array}{l} \Leftrightarrow 3{\log _a}{x_0} + 4{\log _b}{x_0} = 0\\ \Leftrightarrow \dfrac{3}{{{{\log }_{{x_0}}}a}} + \dfrac{4}{{{{\log }_{{x_0}}}b}} = 0\\ \Leftrightarrow \dfrac{{3{{\log }_{{x_0}}}b + 4{{\log }_{{x_0}}}a}}{{{{\log }_{{x_0}}}b.{{\log }_{{x_0}}}a}} = 0\\ \Leftrightarrow {\log _{{x_0}}}{b^3} + {\log _{{x_0}}}{a^4} = 0\\ \Leftrightarrow {\log _{{x_0}}}{a^4}{b^3} = 0\\ \Leftrightarrow {a^4}{b^3} = 1\end{array}\)
Cho hàm số \(f\left( x \right) = \ln \left( {{e^x} + m} \right)\) có \(f'\left( { - \ln 2} \right) = \frac{3}{2}.\) Mệnh đề nào dưới đây đúng?
Ta có: \(f\left( x \right) = \ln \left( {{e^x} + m} \right)\)
Điều kiện: \({e^x} + m > 0.\)
\(\begin{array}{l} \Rightarrow f'\left( x \right) = \frac{{{e^x}}}{{{e^x} + m}}\\ \Rightarrow f'\left( { - \ln 2} \right) = \frac{3}{2} \Leftrightarrow \frac{{{e^{ - \ln 2}}}}{{{e^{ - \ln 2}} + m}} = \frac{3}{2}\\ \Leftrightarrow 2.{e^{ - \ln 2}} = 3.{e^{ - \ln 2}} + 3m\\ \Leftrightarrow {2.2^{ - \ln e}} = {3.2^{ - \ln e}} + 3m\\ \Leftrightarrow 2.\frac{1}{2} - 3.\frac{1}{2} = 3m\\ \Leftrightarrow m = - \dfrac{1}{6}.\\ \Rightarrow m \in \left( { - 2;\,\,0} \right).\end{array}\)
Xét các số thực \(a\), \(b\) thỏa mãn \(a > b > 1\). Tìm giá trị nhỏ nhất \({P_{\min }}\) của biểu thức \(P = \log _{\frac{a}{b}}^2\left( {{a^2}} \right) + 3{\log _b}\left( {\dfrac{a}{b}} \right)\).
Ta có \(P = \log _{\frac{a}{b}}^2\left( {{a^2}} \right) + 3{\log _b}\dfrac{a}{b}\)
\( \Leftrightarrow P = 4\log _{\frac{a}{b}}^2a + 3\left( {{{\log }_b}a - 1} \right)\)\( \Leftrightarrow P = \dfrac{4}{{{{\left( {1 - {{\log }_a}b} \right)}^2}}} + 3\left( {\dfrac{1}{{{{\log }_a}b}} - 1} \right)\)
Đặt \({\log _a}b = t \Rightarrow 0 < t < 1\) . Khi đó \(P = \dfrac{4}{{{{\left( {t - 1} \right)}^2}}} + \dfrac{3}{t} - 3\)
\(P' = \dfrac{{ - 8}}{{{{\left( {t - 1} \right)}^3}}} - \dfrac{3}{{{t^2}}} = 0\) \( \Leftrightarrow 3{t^3} - {t^2} + 9t - 3 = 0\) \( \Rightarrow t = \dfrac{1}{3}\)
\( \Rightarrow {P_{\min }} = 15\).
Cho hai hàm số \(y = \ln \left| {\dfrac{{x - 2}}{x}} \right|\) và \(y = \dfrac{3}{{x - 2}} - \dfrac{1}{x} + 4m - 2020\). Tổng tất cả các giá trị nguyên của tham số m để hai đồ thị hàm số cắt nhau tại một điểm duy nhất bằng:
ĐKXĐ: \(x \ne 0,\,\,x \ne 2\).
Xét phương trình hoành độ giao điểm:
\(\begin{array}{l}\ln \left| {\dfrac{{x - 2}}{x}} \right| = \dfrac{3}{{x - 2}} - \dfrac{1}{x} + 4m - 2020\\ \Leftrightarrow \ln \left| {\dfrac{{x - 2}}{x}} \right| - \dfrac{3}{{x - 2}} + \dfrac{1}{x} = 4m - 2020\end{array}\)
Đặt \(f\left( x \right) = \ln \left| {\dfrac{{x - 2}}{x}} \right| - \dfrac{3}{{x - 2}} + \dfrac{1}{x}\) ta có:
\(\begin{array}{l}f'\left( x \right) = \dfrac{2}{{{x^2}}}:\dfrac{{x - 2}}{x} + \dfrac{3}{{{{\left( {x - 2} \right)}^2}}} - \dfrac{1}{{{x^2}}}\\f'\left( x \right) = \dfrac{2}{{x\left( {x - 2} \right)}} + \dfrac{3}{{{{\left( {x - 2} \right)}^2}}} - \dfrac{1}{{{x^2}}}\\f'\left( x \right) = \dfrac{{2x\left( {x - 2} \right) + 3{x^2} - {{\left( {x - 2} \right)}^2}}}{{{x^2}{{\left( {x - 2} \right)}^2}}}\\f'\left( x \right) = \dfrac{{2{x^2} - 4x + 3{x^2} - {x^2} + 4x - 4}}{{{x^2}{{\left( {x - 2} \right)}^2}}}\\f'\left( x \right) = \dfrac{{4{x^2} - 4}}{{{x^2}{{\left( {x - 2} \right)}^2}}} = 0 \Leftrightarrow x = \pm 1\end{array}\)
BBT:
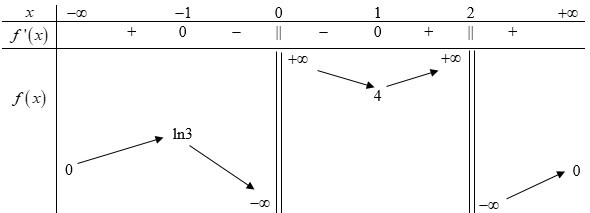
Dựa vào BBT ta thấy để phương trình có nghiệm duy nhất thì \(\left[ \begin{array}{l}4m - 2020 = 0\\4m - 2020 = \ln 3\\4m - 2020 = 4\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 505\\m = \dfrac{{2020 + \ln 3}}{4} \notin \mathbb{Z}\,\,\left( {ktm} \right)\\m = 506\end{array} \right.\).
Vậy tổng các giá trị của \(m\) thỏa mãn yêu cầu bài toán là: \(505 + 506 = 1011\).
Cho $x, y$ là các số thực thỏa mãn \({\log _4}\left( {x + y} \right) + {\log _4}\left( {x - y} \right) \ge 1\). Tìm giá trị nhỏ nhất \({P_{\min }}\) của biểu thức \(P = 2x - y\).
Điều kiện : $x + y >0, x – y > 0$
\({\log _4}\left( {x + y} \right) + {\log _4}\left( {x - y} \right) \ge 1 \Leftrightarrow {\log _4}\left( {{x^2} - {y^2}} \right) \ge 1 \Leftrightarrow {x^2} - {y^2} \ge 4\)
Ta có: $P = 2x - y = \dfrac{{x + y + 3(x - y)}}{2} \ge \sqrt {(x + y).3(x - y)} = \sqrt {3({x^2} - {y^2})} = \sqrt {3.4} = 2\sqrt 3 $
Dấu “=” xảy ra khi:
\(\left\{ \begin{array}{l}x + y = 3\left( {x - y} \right)\\{x^2} - {y^2} = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x + y = 3\left( {x - y} \right)\\3{\left( {x - y} \right)^2} = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x - y = \dfrac{2}{{\sqrt 3 }}\\x + y = 2\sqrt 3 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{1}{{\sqrt 3 }} + \sqrt 3 \\y = \sqrt 3 - \dfrac{1}{{\sqrt 3 }}\end{array} \right.\)
Vậy $Min\,P = 2\sqrt 3 $.
Trên khoảng \((0; + \infty )\), đạo hàm của hàm số \(y = {\log _2}x\) là:
Đạo hàm của hàm số \(y = {\log _2}x\) trên khoảng \((0; + \infty )\) là \({y^\prime } = \dfrac{1}{{x\ln 2}}\)

