Số đường tiệm cận của đồ thị hàm số \(y = \dfrac{{x - 2}}{{\sqrt {{x^2} - 4} }}\) là:
TXĐ: \(D = \left( { - \infty ; - 2} \right) \cup \left( {2; + \infty } \right)\).
Ta có:
\(\begin{array}{l}\mathop {\lim }\limits_{x \to {2^ + }} y = \mathop {\lim }\limits_{x \to {2^ + }} \dfrac{{x - 2}}{{\sqrt {{x^2} - 4} }} = 0\\\mathop {\lim }\limits_{x \to {{\left( { - 2} \right)}^ - }} y = \mathop {\lim }\limits_{x \to {1^ - }} \dfrac{{x - 2}}{{\sqrt {{x^2} - 4} }} = - \infty \end{array}\)
Suy ra \(x = - 2\) là tiệm cận đứng của đồ thị hàm số.
\(\begin{array}{l}\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \dfrac{{x - 2}}{{\sqrt {{x^2} - 4} }} = 1\\\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \dfrac{{x - 2}}{{\sqrt {{x^2} - 4} }} = - 1\end{array}\)
Suy ra \(y = 1,\,\,y = - 1\) là tiệm cận ngang của đồ thị hàm số.
Vậy đồ thị hàm số đã cho có tất cả 3 đường tiệm cận.
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:

Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số \(y = \dfrac{1}{{f\left( x \right) - 1}}\) là
Ta có: \(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \dfrac{1}{{f\left( x \right) - 1}} = \dfrac{1}{{2 - 1}} = 1\), do đó đồ thị hàm số có TCN \(y = 1\).
\(\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \dfrac{1}{{f\left( x \right) - 1}} = 0\), do đó đồ thị hàm số có TCN \(y = 0\).
Số đường tiệm cận đứng của đồ thị hàm số \(y = \dfrac{1}{{f\left( x \right) - 1}}\) là số nghiệm của phương trình \(f\left( x \right) = 1.\)
Dựa vào đồ thị hàm số ta thấy đường thẳng \(y = 1\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại 4 điểm phân biệt nên phương trình \(f\left( x \right) = 1\) có 4 nghiệm phân biệt. Suy ra đồ thị hàm số có 4 đường tiệm cận đứng.
Vậy đồ thị hàm số có tổng cộng 6 đường tiệm cận.
Cho hàm số \(f(x) = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình vẽ bên.
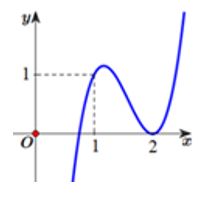
Hỏi đồ thị hàm số \(g(x) = \dfrac{{({x^2} - 3x + 2)\sqrt {x - 1} }}{{x\left[ {{f^2}(x) - f(x)} \right]}}\) có bao nhiêu tiệm cận đứng?
ĐKXĐ: \(x \ge 1,\,\,f\left( x \right) \ne 0,\,\,f\left( x \right) \ne 1\).
\(g(x) = \dfrac{{\left( {{x^2} - 3x + 2} \right)\sqrt {x - 1} }}{{x\left[ {{f^2}\left( x \right) - f\left( x \right)} \right]}} = \dfrac{{\left( {x - 2} \right)\left( {x - 1} \right)\sqrt {x - 1} }}{{x.f\left( x \right)\left( {f\left( x \right) - 1} \right)}}\)
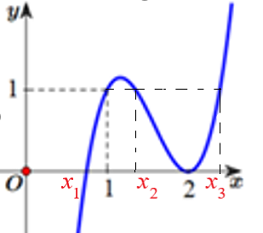
Nhận xét: \(f\left( x \right) = a{x^3} + b{x^2} + cx + d\) là hàm số bậc ba, đồng thời, quan sát đồ thị ta thấy:
+) \(f\left( x \right) = 0\) có 2 nghiệm phân biệt \(x = {x_1}\,\,\left( {0 < {x_1} < 1} \right)\,\,\left( {ktm} \right)\)(nghiệm đơn) và \(x = 2\)(nghiệm kép).
+) \(f\left( x \right) = 1\) có 3 nghiệm phân biệt \(x = 1\) (nghiệm đơn), \(x = {x_2}\,\,\left( {1 < {x_2} < 2} \right)\) (nghiệm đơn) và \(x = {x_3}\,\,\left( {{x_3} > 2} \right)\) (nghiệm đơn).
Khi đó hàm số \(y = g\left( x \right)\) được viết dưới dạng : \(g\left( x \right) = \dfrac{{\left( {x - 2} \right)\left( {x - 1} \right)\sqrt {x - 1} }}{{x.\,a\left( {x - {x_1}} \right){{\left( {x - 2} \right)}^2}.\,a\left( {x - 1} \right)\left( {x - {x_2}} \right)\left( {x - {x_3}} \right)}}\)
Do đó, đồ thị hàm số \(g\left( x \right)\) có 3 đường tiệm cận đứng là: \(x = {x_2},\,\,x = 2,\,\,x = {x_3}.\)
Cho hàm số $y = \dfrac{{a{x^2} + 3ax + 2a + 1}}{{x + 2}}$. Chọn kết luận đúng:
+ Nếu $a = 0$ thì $y = \dfrac{1}{{x + 2}}$, đồ thị hàm số này có tiệm cận đứng $x = - 2$ và tiệm cận ngang $y = 0$ nên A, C sai.
+ Nếu $a \ne 0$ thì $y = ax + a + \dfrac{1}{{x + 2}}$ nên $y = ax + a$ là đường tiệm cận xiên của đồ thị hàm số.
Khi đó $y = ax + a \Leftrightarrow a\left( {x + 1} \right) - y = 0$ luôn đi qua điểm $\left( { - 1;0} \right)$ với mọi $a \ne 0$.
Biết đồ thị hàm số \(y = 2x + \sqrt {a{x^2} + bx + 4} \) có tiệm cận ngang \(y = - 1\). Giá trị \(2a - {b^3}\) bằng
\( - 56\).
\( - 56\).
\( - 56\).
Bước 1: Tìm điều kiện để đồ thị có tiệm cận ngang.
Điều kiện \(a{x^2} + bx + 4 \ge 0\). Để đồ thị hàm số có tiệm cận ngang thì \(a > 0\). Khi đó, ta có
\(\mathop {\lim }\limits_{x \to + \infty } y\)\( = \mathop {\lim }\limits_{x \to + \infty } \left( {2x + \sqrt {a{x^2} + bx + 4} } \right)\)\( = + \infty \)
\(\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \left( {2x + \sqrt {a{x^2} + bx + 4} } \right)\)\( = \mathop {\lim }\limits_{x \to - \infty } \dfrac{{(a - 4){x^2} + bx + 4}}{{\sqrt {a{x^2} + bx + 4} - 2x}} = - 1\)
Bước 2: Tìm a,b rồi tính \(2a - {b^3}\)
\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a - 4 = 0}\\{\dfrac{b}{{ - \sqrt {a }-2 }} = - 1}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = 4}\\{b = 4}\end{array}} \right.} \right.\)
Vậy \(2a - {b^3} = - 56\)

