Bất phương trình logarit

ĐKXĐ: \(x > 0\).

Ta có:

\(\begin{array}{l}{9^{\log _9^2x}} + {x^{{{\log }_9}x}} \le 18\\ \Leftrightarrow {9^{{{\log }_9}x.{{\log }_9}x}} + {x^{{{\log }_9}x}} \le 18\\ \Leftrightarrow {\left( {{9^{{{\log }_9}x}}} \right)^{{{\log }_9}x}} + {x^{{{\log }_9}x}} \le 18\\ \Leftrightarrow {x^{{{\log }_9}x}} + {x^{{{\log }_9}x}} \le 18\\ \Leftrightarrow 2.{x^{{{\log }_9}x}} \le 18\\ \Leftrightarrow {x^{{{\log }_9}x}} \le 9\end{array}\)

Lấy logarit cơ số 9 cả 2 vế bất phương trình ta được:

\(\begin{array}{l}{\log _9}\left( {{x^{{{\log }_9}x}}} \right) \le {\log _9}9\\ \Leftrightarrow {\log _9}x.{\log _9}x \le 1\\ \Leftrightarrow \log _9^2x \le 1\\ \Leftrightarrow  - 1 \le {\log _9}x \le 1\\ \Leftrightarrow \dfrac{1}{9} \le x \le 9\end{array}\)

Kết hợp điều kiện xác định ta có \(x \in \left[ {\dfrac{1}{9};9} \right]\).

Vậy tập nghiệm của bất phương trình là: \(S = \left[ {\dfrac{1}{9};9} \right]\).

Điều kiện : \(x\sqrt {{x^2} + 2}  + 4 - {x^2} > 0 \Leftrightarrow x\left( {\sqrt {{x^2} + 2}  - x} \right) + 4 > 0 \Leftrightarrow x.\dfrac{2}{{\sqrt {{x^2} + 2}  + x}} + 4 > 0\)

\( \Leftrightarrow \dfrac{{2x}}{{\sqrt {{x^2} + 2}  + x}} + \dfrac{{4\left( {\sqrt {{x^2} + 2}  + x} \right)}}{{\sqrt {{x^2} + 2}  + x}} > 0 \Rightarrow 6x + 4\sqrt {{x^2} + 2}  > 0\) (vì \(\sqrt {{x^2} + 2}  > x;\,\forall x\) )

\( \Leftrightarrow 2\sqrt {{x^2} + 2}  >  - 3x \Leftrightarrow \left[ \begin{array}{l} - 3x < 0\\\left\{ \begin{array}{l} - 3x \ge 0\\4\left( {{x^2} + 2} \right) > {\left( { - 3x} \right)^2}\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x > 0\\\left\{ \begin{array}{l}x \le 0\\5{x^2} < 8\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x > 0\\ - \dfrac{{\sqrt {40} }}{5} < x \le 0\end{array} \right.\)

Khi đó ta có \({\log _2}\left( {x\sqrt {{x^2} + 2}  + 4 - {x^2}} \right) + 2x + \sqrt {{x^2} + 2}  \le 1\)

\(\begin{array}{l} \Leftrightarrow {\log _2}\left( {x\left( {\sqrt {{x^2} + 2}  - x} \right) + 4} \right) + 2x + \sqrt {{x^2} + 2}  \le 1\\ \Leftrightarrow {\log _2}\left( {\dfrac{{2x}}{{\sqrt {{x^2} + 2}  + x}} + 4} \right) + 2x + \sqrt {{x^2} + 2}  \le 1\\ \Leftrightarrow {\log _2}\left( {\dfrac{{6x + 4\sqrt {{x^2} + 2} }}{{\sqrt {{x^2} + 2}  + x}}} \right) + 2x + \sqrt {{x^2} + 2}  \le 1\end{array}\)

\(\begin{array}{l} \Leftrightarrow {\log _2}\left( {6x + 4\sqrt {{x^2} + 2} } \right) - {\log _2}\left( {\sqrt {{x^2} + 2}  + x} \right) + 2x + \sqrt {{x^2} + 2}  \le 1\\ \Leftrightarrow {\log _2}\left[ {2\left( {3x + 2\sqrt {{x^2} + 2} } \right)} \right] - {\log _2}\left( {\sqrt {{x^2} + 2}  + x} \right) + 2x + \sqrt {{x^2} + 2}  \le 1\\ \Leftrightarrow {\log _2}2 + {\log _2}\left( {3x + 2\sqrt {{x^2} + 2} } \right) - {\log _2}\left( {\sqrt {{x^2} + 2}  + x} \right) + 2x + \sqrt {{x^2} + 2}  \le 1\\ \Leftrightarrow 1 + {\log _2}\left( {3x + 2\sqrt {{x^2} + 2} } \right) - {\log _2}\left( {\sqrt {{x^2} + 2}  + x} \right) + 2x + \sqrt {{x^2} + 2}  \le 1\\ \Leftrightarrow {\log _2}\left( {3x + 2\sqrt {{x^2} + 2} } \right) + 3x + 2\sqrt {{x^2} + 2}  \le {\log _2}\left( {\sqrt {{x^2} + 2}  + x} \right) + x + \sqrt {{x^2} + 2} \,\left( * \right)\end{array}\)

Xét hàm số \(f\left( t \right) = t + {\log _2}t\,\) với \(t > 0\) ta có \(f'\left( t \right) = 1 + \dfrac{1}{{t.\ln 2}} > 0;\,\forall t > 0\) nên \(f\left( t \right)\) là hàm đồng biến trên \(\left( {0; + \infty } \right)\)

Từ đó

 \(\begin{array}{l}\left( * \right) \Leftrightarrow f\left( {3x + 2\sqrt {{x^2} + 2} } \right) \le f\left( {\sqrt {{x^2} + 2}  + x} \right)\\ \Leftrightarrow 3x + 2\sqrt {{x^2} + 2}  \le \sqrt {{x^2} + 2}  + x\\ \Leftrightarrow \sqrt {{x^2} + 2}  \le  - 2x\\ \Leftrightarrow \left\{ \begin{array}{l} - 2x \ge 0\\{x^2} + 2 \le 4{x^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \le 0\\3{x^2} \ge 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \le 0\\\left[ \begin{array}{l}x \ge \dfrac{{\sqrt 6 }}{3}\\x \le  - \dfrac{{\sqrt 6 }}{3}\end{array} \right.\end{array} \right. \Leftrightarrow x \le  - \dfrac{{\sqrt 6 }}{3}\end{array}\)

Kết hợp điều kiện \(\left[ \begin{array}{l}x > 0\\ - \dfrac{{\sqrt {40} }}{5} < x \le 0\end{array} \right.\)  ta có \( - \dfrac{{\sqrt {40} }}{5} < x \le  - \dfrac{{\sqrt 6 }}{3}\)  hay \( - \sqrt {\dfrac{8}{5}}  < x \le  - \sqrt {\dfrac{2}{3}} \)

Tập nghiệm bất phương trình \(S = \left( { - \sqrt {\dfrac{8}{5}} ; - \sqrt {\dfrac{2}{3}} } \right]\)  nên \(a = \dfrac{8}{5};b = \dfrac{2}{3} \Rightarrow a.b = \dfrac{8}{5}.\dfrac{2}{3} = \dfrac{{16}}{{15}}.\)

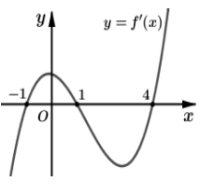
ĐK : \(f\left( x \right) + m + 2 > 0\)

Ta có \({\log _5}\left( {f\left( x \right) + m + 2} \right) + f\left( x \right) > 4 - m\) \( \Leftrightarrow {\log _5}\left( {f\left( x \right) + m + 2} \right) + f\left( x \right) + m + 2 > 6\)  (*)

Xét hàm số \(y = {\log _5}t + t\,\,\,\left( {t > 0} \right)\) có \(y' = \dfrac{1}{{t.\ln 5}} + 1 > 0\) với \(t > 0\)

Nên hàm số \(y = {\log _5}t + t\) đồng biến trên \(\left( {0; + \infty } \right)\), lại có \(y\left( 5 \right) = {\log _5}5 + 5 = 6\)

Nên từ (*) suy ra \(y\left( {f\left( x \right) + m + 2} \right) > y\left( 5 \right) \Leftrightarrow f\left( x \right) + m + 2 > 5 \Leftrightarrow f\left( x \right) > 3 - m\) (1)

Từ hình vẽ ta có BBT của hàm số \(f\left( x \right)\) như sau

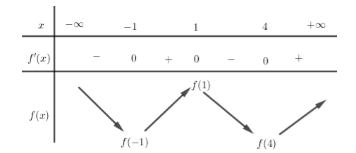
Từ hình vẽ ta có \(\int\limits_{ - 1}^1 {\left| {f'\left( x \right)} \right|} dx < \int\limits_1^4 {\left| {f'\left( x \right)} \right|dx}  \Leftrightarrow \int\limits_{ - 1}^1 {f'\left( x \right)} dx <  - \int\limits_1^4 {f'\left( x \right)dx} \)

\( \Leftrightarrow \left. {f\left( x \right)} \right|_{ - 1}^1 < \left. { - f\left( x \right)} \right|_1^4 \Leftrightarrow f\left( 1 \right) - f\left( { - 1} \right) < f\left( 1 \right) - f\left( 4 \right)\) \( \Leftrightarrow f\left( { - 1} \right) > f\left( 4 \right)\) (2)

Từ (1) ; (2) và BBT ta thấy để phương trình đã cho đúng với \(x \in \left( { - 1;4} \right)\) suy ra \(3 - m \le f\left( 4 \right) \Leftrightarrow m \ge 3 - f\left( 4 \right).\)

ĐK: \({x^2} + 6x + 5 + m > 0.\)

\(\begin{array}{l}{\log _7}\left( {{x^2} + 2x + 2} \right) + 1 > {\log _7}\left( {{x^2} + 6x + 5 + m} \right)\\ \Leftrightarrow {\log _7}7\left( {{x^2} + 2x + 2} \right) > {\log _7}\left( {{x^2} + 6x + 5 + m} \right)\\ \Leftrightarrow 7\left( {{x^2} + 2x + 2} \right) > {x^2} + 6x + 5 + m\\ \Leftrightarrow 7{x^2} + 14x + 14 - {x^2} - 6x - 5 - m > 0\\ \Leftrightarrow 6{x^2} + 8x + 9 - m > 0\end{array}\)

Bất phương trình đã cho có tập nghiệm chứa \(\left( {1;3} \right)\)

\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}{x^2} + 6x + 5 + m > 0,\forall x \in \left( {1;3} \right)\\6{x^2} + 8x + 9 - m > 0,\forall x \in \left( {1;3} \right)\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}m >  - {x^2} - 6x - 5,\forall x \in \left( {1;3} \right)\\m < 6{x^2} + 8x + 9,\forall x \in \left( {1;3} \right)\end{array} \right.\,\,\left( * \right)\end{array}\)

\( \Leftrightarrow \left\{ \begin{array}{l}m \ge \mathop {\max }\limits_{\left[ {1;3} \right]} f\left( x \right)\\m \le \mathop {\min }\limits_{\left[ {1;3} \right]} g\left( x \right)\end{array} \right.\)

với \(f\left( x \right) =  - {x^2} - 6x - 5\) và \(g\left( x \right) = 6{x^2} + 8x + 9\)

Ta có:

\(f'\left( x \right) =  - 2x - 6 = 0\) \( \Leftrightarrow x =  - 3 \notin \left( {1;3} \right)\) và \(f'\left( x \right) < 0,\forall x \in \left( {1;3} \right)\) nên hàm số \(y = f\left( x \right)\) nghịch biến trên \(\left( {1;3} \right)\)

\( \Rightarrow \mathop {\max }\limits_{\left[ {1;3} \right]} f\left( x \right) = f\left( 1 \right) =  - 12\) \( \Rightarrow m \ge  - 12\)

\(g'\left( x \right) = 12x + 8 = 0\) \( \Leftrightarrow x =  - \frac{2}{3} \notin \left( {1;3} \right)\) và \(g'\left( x \right) > 0,\forall x \in \left( {1;3} \right)\) nên hàm số \(y = g\left( x \right)\) đồng biến trên \(\left( {1;3} \right)\)

\( \Rightarrow \mathop {\min }\limits_{\left[ {1;3} \right]} g\left( x \right) = g\left( 1 \right) = 23\) \( \Rightarrow m \le 23\)

Vậy \( - 12 \le m \le 23\).

Mà \(m \in \mathbb{Z} \Rightarrow m \in \left\{ { - 12; - 11;...;23} \right\}\) hay có \(23 - \left( { - 12} \right) + 1 = 36\) giá trị.

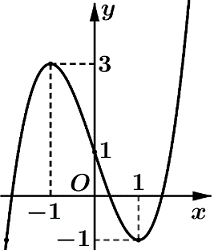
ĐKXĐ: \( - x > 0 \Leftrightarrow x < 0\).

Ta có: \(f\left( x \right) < \ln \left( { - x} \right) + m \Leftrightarrow m > f\left( x \right) - \ln \left( { - x} \right)\) (*)

Xét hàm số \(g\left( x \right) = f\left( x \right) - \ln \left( { - x} \right)\) trên khoảng \(\left( { - 1; - \dfrac{1}{e}} \right)\) có:

\(\,g'\left( x \right) = f'\left( x \right) - \dfrac{{ - 1}}{{ - x}} = f'\left( x \right) - \dfrac{1}{x}\)

Ta biểu diễn đồ thị hàm số \(y = \dfrac{1}{x}\) (nét màu đỏ) trên hình vẽ như sau:

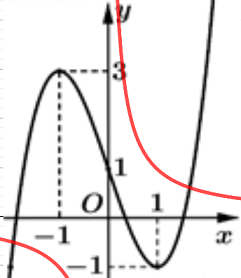
Quan sát đồ thị hàm số ta thấy

\(\,g'\left( x \right) = f'\left( x \right) - \dfrac{1}{x} > 0,\,\,\forall x \in \)\(\left( { - 1; - \dfrac{1}{e}} \right) \Rightarrow \) Hàm số \(y = g\left( x \right)\) đồng biến trên \(\left( { - 1; - \dfrac{1}{e}} \right)\).

Ta có: \(\left\{ \begin{array}{l}g\left( { - 1} \right) = f\left( { - 1} \right) - \ln \left( 1 \right) = 1\\g\left( { - \dfrac{1}{e}} \right) = f\left( { - \dfrac{1}{e}} \right) - \ln \dfrac{1}{e} = 2 + 1 = 3\end{array} \right.\) .

Để (*) nghiệm đúng với mọi \(x \in \left( { - 1; - \dfrac{1}{e}} \right)\) thì \( \Leftrightarrow m \ge \mathop {max}\limits_{\left[ { - 1; - \dfrac{1}{e}} \right]} g\left( x \right) \Leftrightarrow m \ge 3.\)

\(\begin{array}{l}\,\,\,\,\,\,{\log _{\dfrac{2}{3}}}\left( {3x - 2} \right) > {\log _{\dfrac{2}{3}}}\left( {2x + 1} \right)\\ \Leftrightarrow 0 < 3x - 2 < 2x + 1\\ \Leftrightarrow \left\{ \begin{array}{l}x > \dfrac{2}{3}\\x - 3 < 0\end{array} \right. \Leftrightarrow \dfrac{2}{3} < x < 3\end{array}\)

Vậy tập nghiệm của bất phương trình đã cho là: \(S = \left( {\dfrac{2}{3};\,\,3} \right).\)

Bước 1: Đặt \(t = 2a + b\;\left( {t \ge 0} \right)\), đưa bất phương trình về dạng \(f\left( t \right) \ge 0\)

Đặt \(t = 2a + b\;\left( {t \ge 0} \right)\), ta có giả thiết đã cho tương đương với \(f\left( t \right) = {\log _2}t - t + 1 \ge 0\)

Ta có \(f'\left( t \right) = \dfrac{1}{{t\ln 2}} - 1 > 0 \Leftrightarrow t < \dfrac{1}{{\ln 2}}\) . Hàm số đồng biến trên \(\left( {0;\dfrac{1}{{\ln 2}}} \right)\)

Bước 2: Chứng minh \(t \ge 1\).

Ta chứng minh \(t \ge 1\) .

Thật vậy, giả sử \(t < 1\) thì \(f\left( t \right) < f\left( 1 \right) = 0\) (mâu thuẫn)

Vậy \(2a + b \ge 1\)

Áp dụng BĐT Cauchy – Schwarz ta có

\(\begin{array}{l}{\left( {2a + b} \right)^2} \le \left( {{2^2} + {1^2}} \right)\left( {{a^2} + {b^2}} \right) = 5\left( {{a^2} + {b^2}} \right)\\ \Rightarrow {a^2} + {b^2} \ge \dfrac{{{{\left( {2a + b} \right)}^2}}}{5} \ge \dfrac{1}{5}\end{array}\)

Dấu bằng xảy ra \(\left\{ \begin{array}{l}2a + b = 1\\\dfrac{a}{2} = \dfrac{b}{1}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \dfrac{2}{5}\\b = \dfrac{1}{5}\end{array} \right.\)

Bước 1: Đặt \(f\left( x \right) = {\log _{2020}}\left( {x + {y^2}} \right) + {\log _{2021}}\left( {{y^2} + y + 64} \right) - {\log _4}\left( {x - y} \right)\) và tìm điều kiện xác định.

Đặt \(f\left( x \right) = {\log _{2020}}\left( {x + {y^2}} \right) + {\log _{2021}}\left( {{y^2} + y + 64} \right) - {\log _4}\left( {x - y} \right)\) (coi \(y\) là tham số).

Điều kiện xác định của \(f\left( x \right)\) là:

\(\left\{ {\begin{array}{*{20}{c}}{x + {y^2} > 0}\\{{y^2} + y + 64 > 0}\\{x - y > 0}\end{array}} \right.\)

Do \(x,\;y\) nguyên nên \(x > y \ge  - {y^2}\). Cũng vì \(x,\;y\) nguyên nên ta chỉ xét \(f\left( x \right)\) trên nửa khoảng \(\left[ {y + 1; + \infty } \right)\).

Bước 2: Xét hàm số trên \(\left[ {y + 1; + \infty } \right)\)

Ta có:

\(f'\left( x \right) = \dfrac{1}{{\left( {x + {y^2}} \right)\ln 2020}} - \dfrac{1}{{\left( {x - y} \right)\ln 2021}} - \dfrac{1}{{\left( {x - y} \right)\ln 4}} < 0,\;\forall x \ge y + 1\)

Bước 3: Lập bảng biến thiên

Ta có bảng biến thiên của hàm số \(f\left( x \right):\)

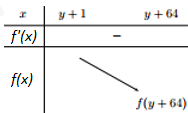
Bước 4: Tìm y nguyên \(f\left( {y + 64} \right) < 0\)

Yêu cầu bài toán trở thành:

\(f\left( {y + 64} \right) < 0\)

\( \Leftrightarrow {\log _{2020}}\left( {{y^2} + y + 64} \right) + {\log _{2021}}\left( {{y^2} + y + 64} \right) < {\log _4}64\)

\( \Leftrightarrow {\log _{2021}}\left( {{y^2} + y + 64} \right)\left( {{{\log }_{2020}}2021 + 1} \right) < 3\)

\( \Leftrightarrow {y^2} + y + 64 - {2021^{\dfrac{3}{{{{\log }_{2020}}2021 + 1}}}} < 0\)

\( \Leftrightarrow  - 301,76 < y < 300,76\)

Mà \(y\) nguyên nên \(y \in \left\{ { - 301; - 300; \ldots ;299;300} \right\}\).

Vậy có 602 giá trị nguyên của \(y\) thỏa mãn yêu cầu.

\(\begin{array}{l}{\log _2}\left( {{x^2} + 2x + m} \right) - 2{\log _2}\left( {2x - 1} \right) > 0 \Leftrightarrow \left\{ \begin{array}{l}{\log _2}\left( {{x^2} + 2x + m} \right) > {\log _2}{\left( {2x - 1} \right)^2}\\x > \dfrac{1}{2}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{x^2} + 2x + m > {\left( {2x - 1} \right)^2}\\x > \dfrac{1}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3{x^3} - 6x + 1 < m\\x > \dfrac{1}{2}\end{array} \right.\end{array}\)

Xét bất phương trình \(3{x^3} - 6x + 1 < m\)(1) với \(x > \dfrac{1}{2}\)

Bảng biến thiên của hàm số \(y = 3{x^3} - 6x + 1\) trên \(\left( {\dfrac{1}{2}; + \infty } \right)\)

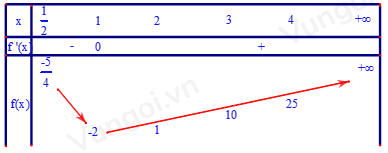
Bất phương trình (1) có nghiệm thì \(m >  - 2\) khi đó (1) luôn có 1 nghiệm nguyên x=1

Vậy nếu (1) có đúng 2 nghiệm nguyên thì 2 nghiệm nguyên đó chắc chắn là \(x = 1,x = 2\)

$=>f(2)<m=>1<m$

Khi đó, \(2 \le m \le 10\)

Vậy có tất cả 9 giá trị nguyên cần tìm

Bước 1: Điều kiện

\({x^2} + 4x + 2 + m > 0\)

Bước 2:

Ta có:

\(\begin{array}{l}{\log _5}\left( {{x^2} + 2x + 3} \right) > {\log _5}\left( {{x^2} + 4x + 2 + m} \right) - 1\\ \Leftrightarrow {\log _5}\left( {{x^2} + 2x + 3} \right) + {\log _5}5 > {\log _5}\left( {{x^2} + 4x + 2 + m} \right)\\ \Leftrightarrow {\log _5}\left[ {5\left( {{x^2} + 2x + 3} \right)} \right] > {\log _5}\left( {{x^2} + 4x + 2 + m} \right)\\ \Leftrightarrow 5\left( {{x^2} + 2x + 3} \right) > {x^2} + 4x + 2 + m\\ \Leftrightarrow 4{x^2} + 6x + 13 - m > 0\end{array}\)

Bước 3:

Vì \(\left( {1;2} \right) \subset S\) nên bài toán trở thành tìm m nguyên để hệ bất phương trình

\(\left\{ \begin{array}{l}{x^2} + 4x + 2 + m > 0\\4{x^2} + 6x + 13 - m > 0\end{array} \right.\) nghiệm đúng với mọi \(x \in \left( {1;2} \right)\)

Tương đương với hai bất phương trình: \({x^2} + 4x + 2 + m > 0\) nghiệm đúng với mọi \(x \in \left( {1;2} \right)\) và bất phương trình \(4{x^2} + 6x + 13 - m > 0\) nghiệm đúng với mọi \(x \in \left( {1;2} \right)\)

Ta xét \({x^2} + 4x + 2 + m > 0\) nghiệm đúng với mọi \(x \in \left( {1;2} \right)\)

\( \Leftrightarrow m >  - {x^2} - 4x - 2\forall x \in \left( {1;2} \right)\)

\( \Leftrightarrow m > \mathop {\max }\limits_{\left[ {1;2} \right]} \left( { - {x^2} - 4x - 2} \right)\)

\(m >  - 7\)

Tương tự với \(4{x^2} + 6x + 13 - m > 0\) nghiệm đúng với mọi \(x \in \left( {1;2} \right)\)

Ta có \(m < 4{x^2} + 6x + 13\forall x \in \left( {1;2} \right)\)

\(\begin{array}{l} \Leftrightarrow m < \mathop {\min }\limits_{\left[ {1;2} \right]} \left( {4{x^2} + 6x + 13} \right)\\ \Leftrightarrow m < 23\end{array}\)

Vậy \( - 7 < m < 23\)

Vì m nguyên nên m là các số nguyên thỏa mãn \( - 6 \le m \le 22\), tức là có 22-(-6)+1=29 giá trị của m thỏa mãn bài toán.

Bước 1: Đặt \({\log _4}2x = a;{\log _6}2x = b\)

TXĐ: \(D = \left( {0; + \infty } \right)\)

Đặt \({\log _4}2x = a;{\log _6}2x = b\)

Bước 2: Giải bất phương trình

BPT trở thành:

\(\begin{array}{l}a + b \ge 1 + ab \Leftrightarrow a - 1 + b - ab \ge 0\\ \Leftrightarrow \left( {a - 1} \right) - b\left( {a - 1} \right) \ge 0\\ \Leftrightarrow \left( {a - 1} \right)\left( {b - 1} \right) \le 0\end{array}\)

\(\begin{array}{l} \Leftrightarrow \left( {{{\log }_4}2x - 1} \right)\left( {{{\log }_6}2x - 1} \right) \le 0\\ \Leftrightarrow {\log _4}\dfrac{{2x}}{4}.{\log _6}\dfrac{{2x}}{6} \le 0\\ \Leftrightarrow {\log _4}\dfrac{x}{2}.{\log _6}\dfrac{x}{3} \le 0\\ \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}{\log _4}\dfrac{x}{2} \ge 0\\{\log _6}\dfrac{x}{3} \le 0\end{array} \right.\\\left\{ \begin{array}{l}{\log _4}\dfrac{x}{2} \le 0\\{\log _6}\dfrac{x}{3} \ge 0\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}\dfrac{x}{2} \ge 1\\\dfrac{x}{3} \le 1\end{array} \right.\\\left\{ \begin{array}{l}\dfrac{x}{2} \le 1\\\dfrac{x}{3} \ge 1\end{array} \right.\end{array} \right.\end{array}\)

\( \Leftrightarrow \left[ \begin{array}{l}2 \le x \le 3\\\left\{ \begin{array}{l}x \le 2\\x \ge 3\end{array} \right.\left( L \right)\end{array} \right.\)

Vậy có 2 nghiệm nguyên của bất phương trình.

Điều kiện: \(\left\{ \begin{array}{l}{x^2} + y > 0\\x + y > 0\end{array} \right..\)

Ta có: \({\log _3}\left( {{x^2} + y} \right) \ge {\log _2}\left( {x + y} \right)\)

\(\begin{array}{l} \Leftrightarrow {x^2} + y \ge {3^{{{\log }_2}\left( {x + y} \right)}}\\ \Leftrightarrow {x^2} + y \ge {\left( {x + y} \right)^{{{\log }_2}3}}\,\,\,\,\left( 1 \right)\end{array}\)

Điều kiện: \(x + y \ge 1\,\,\,\left( {do\,\,\,x,\,\,y \in \mathbb{Z},\,\,x + y > 0} \right).\)  

Đặt \(t = x + y\,\,\,\left( {t \ge 1} \right)\)

\(\begin{array}{l} \Rightarrow \left( 1 \right) \Leftrightarrow {x^2} + t - x \ge {t^{{{\log }_2}3}}\\ \Leftrightarrow {x^2} - x \ge {t^{{{\log }_2}3}} - t\,\,\,\,\left( 2 \right)\end{array}\)

Để \(\left( 1 \right)\) không có quá \(255\) nghiệm nguyên \(y\) \( \Leftrightarrow \,\,\left( 2 \right)\) có không quá \(255\) nghiệm nguyên dương \(t\)

Đặt \(A = f\left( {255} \right)\) với \(f\left( t \right) = {t^{{{\log }_2}3}} - t\)

Ta có: \(f'\left( t \right) = {\log _2}3.{t^{{{\log }_2}3 - 1}} - 1 > 0\,\,\,\forall t > 1\)

\( \Rightarrow f\left( t \right)\) là hàm số đồng biến trên \(\left[ {1; + \infty } \right)\)

\( \Rightarrow \left( 2 \right) \Leftrightarrow 1 \le t \le {f^{ - 1}}\left( {{x^2} - x} \right)\) với \({x^2} - x \ge 0\)

\( \Rightarrow \left( 2 \right)\) có không quá \(255\) nghiệm nguyên \( \Leftrightarrow {f^{ - 1}}\left( {{x^2} - x} \right) \le 255\)

\( \Leftrightarrow {x^2} - x \le 255\)\( \Leftrightarrow {x^2} - x - 255 \le 0\) \( \Leftrightarrow  - 78 \le x \le 79\)

Lại có: \(x \in \mathbb{Z}\) \( \Rightarrow \) Có \(158\) số nguyên \(x\) thỏa mãn bài toán.