Câu hỏi:
2 năm trước
Có bao nhiêu giá trị nguyên của tham số m để tập nghiệm của bất phương trình \({\log _2}\left( {{x^2} + 2x + m} \right) - 2{\log _2}\left( {2x - 1} \right) > 0\) chứa đúng hai số nguyên?
Trả lời bởi giáo viên
Đáp án đúng: c
\(\begin{array}{l}{\log _2}\left( {{x^2} + 2x + m} \right) - 2{\log _2}\left( {2x - 1} \right) > 0 \Leftrightarrow \left\{ \begin{array}{l}{\log _2}\left( {{x^2} + 2x + m} \right) > {\log _2}{\left( {2x - 1} \right)^2}\\x > \dfrac{1}{2}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{x^2} + 2x + m > {\left( {2x - 1} \right)^2}\\x > \dfrac{1}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3{x^3} - 6x + 1 < m\\x > \dfrac{1}{2}\end{array} \right.\end{array}\)
Xét bất phương trình \(3{x^3} - 6x + 1 < m\)(1) với \(x > \dfrac{1}{2}\)
Bảng biến thiên của hàm số \(y = 3{x^3} - 6x + 1\) trên \(\left( {\dfrac{1}{2}; + \infty } \right)\)
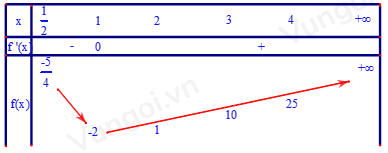
Bất phương trình (1) có nghiệm thì \(m > - 2\) khi đó (1) luôn có 1 nghiệm nguyên x=1
Vậy nếu (1) có đúng 2 nghiệm nguyên thì 2 nghiệm nguyên đó chắc chắn là \(x = 1,x = 2\)
$=>f(2)<m=>1<m$
Khi đó, \(2 \le m \le 10\)
Vậy có tất cả 9 giá trị nguyên cần tìm
Hướng dẫn giải:
- Giải bất phương trình cùng cơ số
- Xét bất phương trình \(3{x^3} - 6x + 1 < m\)(1) với \(x > \dfrac{1}{2}\)
- Lập bảng biến thiên và tìm các nghiệm nguyên.
