Cho hệ phương trình \(\left\{ \begin{array}{l}{6^x} - {2.3^y} = 2\\{6^x}{.3^y} = 12\end{array} \right.\) có nghiệm \(\left( {x;y} \right)\). Chọn kết luận đúng:
Đặt \(\left\{ \begin{array}{l}{6^x} = a > 0\\{3^y} = b > 0\end{array} \right.\) thì hệ trở thành: \(\left\{ \begin{array}{l}a - 2b = 2\\ab = 12\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2b + 2\\{b^2} + b - 6 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2b + 2\\b = 2(TM);b = - 3(L)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 6\\b = 2\end{array} \right.\)
Do đó \(\left\{ \begin{array}{l}{6^x} = 6\\{3^y} = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1 \in Z\\y = {\log _3}2 \in I\end{array} \right.\)
Cho hệ phương trình $\left\{ \begin{array}{l}{\left( {\dfrac{2}{3}} \right)^{2x - y}} + 6{\left( {\dfrac{2}{3}} \right)^{\frac{{2x - y}}{2}}} - 7 = 0\\{3^{{{\log }_9}\left( {x - y} \right)}} = 1\end{array} \right.$. Chọn khẳng định đúng:
ĐKXĐ: \(x - y > 0 \Leftrightarrow x > y\) nên A sai.
Xét phương trình thứ nhất của hệ: ${\left( {\dfrac{2}{3}} \right)^{2x - y}} + 6{\left( {\dfrac{2}{3}} \right)^{\frac{{2x - y}}{2}}} - 7 = 0$.
Đặt \(t = {\left( {\dfrac{2}{3}} \right)^{\frac{{2x - y}}{2}}} > 0\) thì phương trình trở thành \({t^2} + 6t - 7 = 0 \Leftrightarrow \left[ \begin{array}{l}t = 1(TM)\\t = - 7(L)\end{array} \right.\)
Suy ra \({\left( {\dfrac{2}{3}} \right)^{\frac{{2x - y}}{2}}} = 1 \Leftrightarrow 2x - y = 0\)
Phương trình thứ hai của hệ ${3^{{{\log }_9}\left( {x - y} \right)}} = 1 \Leftrightarrow {\log _9}\left( {x - y} \right) = 0 \Leftrightarrow x - y = 1$.
Từ đó ta có: \(\left\{ \begin{array}{l}2x - y = 0\\x - y = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 1\\y = - 2\end{array} \right.\left( {TM} \right)\)
Vậy hệ có nghiệm duy nhất \(\left( { - 1; - 2} \right)\).
Cho hệ phương trình \(\left\{ \begin{array}{l}{2^x} + 2x = 3 + y\\{2^y} + 2y = 3 + x\end{array} \right.\). Gọi \(\left( {{x_0};{y_0}} \right)\) là nghiệm của hệ, chọn mệnh đề đúng:
Trừ vế với vế của phương trình đầu cho phương trình hai ta được:
${2^x} - {2^y} + 2x - 2y = y - x \Leftrightarrow {2^x} + 3x = {2^y} + 3y$
Xét hàm số \(f\left( t \right) = {2^t} + 3t\) có \(f'\left( t \right) = {2^t}\ln 2 + 3 > 0,\forall t \in R\) nên hàm số đồng biến trên \(R\).
Do đó \(f\left( x \right) = f\left( y \right) \Leftrightarrow x = y \Rightarrow {2^x} + 2x = 3 + y \Leftrightarrow {2^x} + x = 3\)
Xét hàm \(g\left( x \right) = {2^x} + x\) có \(g'\left( x \right) = {2^x}\ln 2 + 1 > 0,\forall x \in R\) nên hàm số \(y = g\left( x \right)\) đồng biến trên \(R\).
Dễ thấy \(g\left( 1 \right) = 3\) nên \(x = 1\) là nghiệm duy nhất của phương trình hay \(\left( {1;1} \right)\) là nghiệm duy nhất của hệ.
Vậy \({x_0} = {y_0} = 1 > 0\).
Số nghiệm của hệ phương trình \(\left\{ \begin{array}{l}{3^x} - {3^y} = y - x\\{x^2} + xy + {y^2} = 12\end{array} \right.\) là:
Phương trình \({3^x} - {3^y} = y - x \Leftrightarrow {3^x} + x = {3^y} + y\).
Xét hàm \(f\left( t \right) = {3^t} + t\) có \(f'\left( t \right) = {3^t}\ln 3 + 1 > 0,\forall t \in R\) nên hàm số đồng biến trên \(R\).
Do đó \(f\left( x \right) = f\left( y \right) \Leftrightarrow x = y\).
Thay \(y = x\) vào phương trình \({x^2} + xy + {y^2} = 12\) ta được: \({x^2} + {x^2} + {x^2} = 12 \Leftrightarrow 3{x^2} = 12 \Leftrightarrow x = \pm 2 \Rightarrow y = \pm 2\)
Vậy hệ có nghiệm \(\left( {2;2} \right),\left( { - 2; - 2} \right)\).
Số nghiệm của hệ \(\left\{ \begin{array}{l}{2^x} = 2y\\{2^y} = 2x\end{array} \right.\) là:
Trừ phương trình 1 cho 2 vế với vế ta được:
\({2^x} - {2^y} = 2y - 2x \Leftrightarrow {2^x} + 2x = {2^y} + 2y\)
Xét hàm \(f\left( t \right) = {2^t} + 2t\) có \(f'\left( t \right) = {2^t}\ln 2 + 2 > 0,\forall t \in R\) nên hàm số \(f\left( t \right)\) đồng biến trên \(R\).
Do đó \(f\left( x \right) = f\left( y \right) \Leftrightarrow x = y\).
Thay \(y = x\) vào phương trình \({2^x} = 2y\) ta được \({2^x} = 2x \Leftrightarrow {2^x} - 2x = 0\).
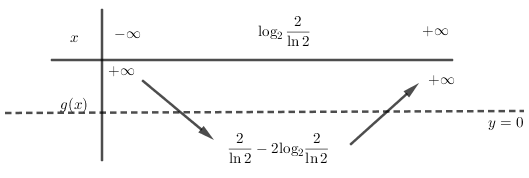
Xét hàm \(y=g\left( x \right) = {2^x} - 2x\) có \(g'\left( x \right) = {2^x}\ln 2 - 2 = 0 \Leftrightarrow x = {\log _2}\dfrac{2}{{\ln 2}}\).
Suy ra \(g'\left( x \right) > 0 \Leftrightarrow x > {\log _2}\dfrac{2}{{\ln 2}};\) \(g'\left( x \right) < 0 \Leftrightarrow x < {\log _2}\dfrac{2}{{\ln 2}}\)
\( \Rightarrow x = {\log _2}\dfrac{2}{{\ln 2}}\) là điểm cực tiểu của hàm số\( \Rightarrow {y_{CT}} = {2^{{{\log }_2}\frac{2}{{\ln 2}}}} - 2{\log _2}\dfrac{2}{{\ln 2}} = \dfrac{2}{{\ln 2}} - 2{\log _2}\dfrac{2}{{\ln 2}} < 0\)
Mặt khác \(\mathop {\lim }\limits_{x \to \pm \infty } g(x) = + \infty \) suy ra đường thẳng \(y = 0\) cắt đồ thị hàm số \(y = g\left( x \right)\) tại \(2\) điểm phân biệt.
Vậy số nghiệm của hệ là \(2\)
Gọi \(m\) là giá trị thực thỏa mãn hệ \(\left\{ \begin{array}{l}{2^{\left| x \right|}} - {2^y} = y - \left| x \right|\left( {m + 1} \right)\\{x^2} + y = {m^2}\end{array} \right.\) có nghiệm duy nhất, khi đó giá trị của \(m\) thỏa mãn:
Ta thấy: nếu \(\left( {{x_0};{y_0}} \right)\) là nghiệm của hệ thì \(\left( { - {x_0};{y_0}} \right)\) cũng là nghiệm của hệ, do đó \(\left( {0;{y_0}} \right)\) cũng là nghiệm của hệ.
Với \(x = 0\) thì \(\left\{ \begin{array}{l}1 - {2^y} = y\\y = {m^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = {m^2}\\{2^y} + y = 1\end{array} \right.\).
Xét hàm \(f\left( t \right) = {2^t} + t\) có \(f'\left( t \right) = {2^t}\ln 2 + 1 > 0,\forall t \in R\) nên phương trình \({2^y} + y = 1\) có nghiệm duy nhất \(y = 0 \Rightarrow {m^2} = 0 \Leftrightarrow m = 0\).
Với \(m = 0\) thì hệ trở thành \(\left\{ \begin{array}{l}{2^{\left| x \right|}} - {2^y} = y - \left| x \right|\\{x^2} + y = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{2^{\left| x \right|}} + \left| x \right| = {2^y} + y\\{x^2} + y = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left| x \right| = y\\{y^2} + y = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 0\\x = 0\end{array} \right.\)
Do đó hệ có nghiệm duy nhất \(\left( {x;y} \right) = \left( {0;0} \right)\)nếu \(m = 0\).

