Cho hai số phức \({z_1},{z_2}\) thỏa mãn \(\left| {{z_1}} \right| = 6,\left| {{z_2}} \right| = 2\). Gọi \(M,N\) lần lượt là các điểm biểu diễn của số phức \({z_1}\) và số phức \(i{z_2}\). Biết \(\widehat {MON} = {60^0}\). Tính \(T = \left| {z_1^2 + 9z_2^2} \right|\).
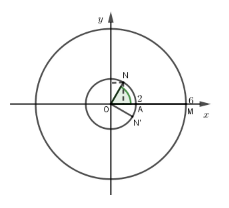
Ta chọn \({z_1} = 6\) có điểm biểu diễn là \(M\left( {6;0} \right)\).
Khi đó \(\widehat {MON} = {60^0}\) nên chọn \(N\left( {1;\sqrt 3 } \right)\) (hình vẽ) biểu diễn số phức \(i{z_2}\)
Suy ra điểm \(N'\left( {\sqrt 3 ; - 1} \right)\) biểu diễn số phức \({z_2}\) hay \({z_2} = \sqrt 3 - i\).
Khi đó \(T = \left| {z_1^2 + 9z_2^2} \right| = \left| {{6^2} + 9{{\left( {\sqrt 3 - i} \right)}^2}} \right| = 36\sqrt 3 \).
Cho hai số phức \({z_1} = 3 + i,\)\({z_2} = - 1 + 2i\). Trong mặt phẳng tọa độ, điểm biểu diễn cho số phức \(w = 2{z_1} - {z_2}\) là:
Ta có
\(\begin{array}{l}w = 2{z_1} - {z_2}\\\,\,\,\,\, = 2\left( {3 + i} \right) - \left( { - 1 + 2i} \right)\\\,\,\,\,\, = 6 + 2i + 1 - 2i = 7\end{array}\)
Vậy điểm biểu diễn của số phức \(w\) là \(M\left( {7;0} \right)\).
Trong mặt phẳng phức, tập hợp các điểm biểu diễn các số phức z thỏa mãn \(z.\bar z = 1\) là:
Bước 1:
Gọi \(z = x + yi\left( {x;y \in R} \right)\) khi đó \(\overline z = x - yi\)
Bước 2:
Ta có: \(z.\overline z = 1 \Leftrightarrow \left( {x + yi} \right)\left( {x - yi} \right) = 1\) \( \Leftrightarrow {x^2} - {\left( {yi} \right)^2} = 1\) \( \Leftrightarrow {x^2} + {y^2} = 1\)
Vậy tập hợp điểm biểu diễn số phức \(z\) là một đường tròn.
Trong mặt phẳng phức, gọi A, B, C, D lần lượt là các điểm biểu diễn các số phức \({z_1} = - 1 + i,\) \(\,\,{z_2} = 1 + 2i,\)\({z_3} = 2 - i,\)\({z_4} = - 3i\). Gọi S diện tích tứ giác ABCD. Tính S.
Ta có: \(A\left( { - 1;1} \right);\,\,B\left( {1;2} \right);\,\,C\left( {2; - 1} \right);\,\,D\left( {0; - 3} \right)\)
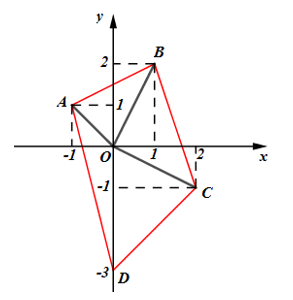
Phương trình AB: \(\dfrac{{x + 1}}{{1 + 1}} = \dfrac{{y - 1}}{{2 - 1}} \Leftrightarrow x + 1 = 2y - 2 \Leftrightarrow x - 2y + 3 = 0 \Rightarrow d\left( {O;AB} \right) = \dfrac{3}{{\sqrt 5 }};\,\,AB = \sqrt 5 \)
\( \Rightarrow {S_{\Delta OAB}} = \dfrac{1}{2}d\left( {O;AB} \right).AB = \dfrac{1}{2}.\dfrac{3}{{\sqrt 5 }}.\sqrt 5 = \dfrac{3}{2}\)
Phương trình BC: \(\dfrac{{x - 1}}{{2 - 1}} = \dfrac{{y - 2}}{{ - 1 - 2}} \Leftrightarrow - 3x + 3 = y - 2 \Leftrightarrow 3x + y - 5 = 0 \Rightarrow d\left( {O;BC} \right) = \dfrac{5}{{\sqrt {10} }};\,\,BC = \sqrt {10} \)
\( \Rightarrow {S_{\Delta OBC}} = \dfrac{1}{2}d\left( {O;BC} \right).BC = \dfrac{1}{2}.\dfrac{5}{{\sqrt {10} .\sqrt {10} }} = \dfrac{5}{2}\)
Phương trình CD: \(\dfrac{{x - 2}}{{0 - 2}} = \dfrac{{y + 1}}{{ - 3 + 1}} \Leftrightarrow - 2x + 4 = - 2y - 2 \Leftrightarrow x - y - 3 = 0 \Rightarrow d\left( {O;CD} \right) = \dfrac{3}{{\sqrt 2 }};\,\,CD = 2\sqrt 2 \)
\( \Rightarrow {S_{\Delta OCD}} = \dfrac{1}{2}.\dfrac{3}{{\sqrt 2 }}.2\sqrt 2 = 3\)
Phương trình AD: \(\dfrac{{x + 1}}{{0 + 1}} = \dfrac{{y - 1}}{{ - 3 - 1}} \Leftrightarrow - 4x - 4 = y - 1 \Leftrightarrow 4x + y + 3 = 0 \Rightarrow d\left( {O;AD} \right) = \dfrac{3}{{\sqrt {17} }};\,\,AD = \sqrt {17} \)
\( \Rightarrow {S_{\Delta OAD}} = \dfrac{1}{2}.\dfrac{3}{{\sqrt {17} }}.\sqrt {17} = \dfrac{3}{2}\)
Vậy \(S = {S_{\Delta OAB}} + {S_{\Delta OBC}} + {S_{\Delta OCD}} + {S_{\Delta OAD}} = \dfrac{{17}}{2}\).
Cho các số phức \({z_1} = 2,{z_2} = - 4i,{z_3} = 2 - 4i\) có điểm biểu diễn tương ứng trên mặt phẳng tọa độ Oxy là A, B, C. Diện tích tam giác ABC bằng
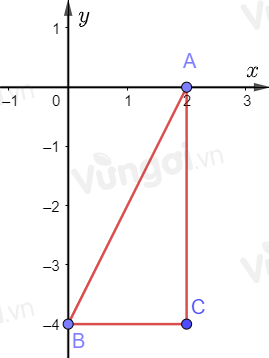
Các điểm biểu diễn trên mặt phẳng tọa độ: A(2;0), B(0;-4), C(2;-4).
Ta thấy tam giác ABC vuông tại C với độ dài hai cạnh góc vuông là: 2 và 4.
\({S_{ABC}} = \dfrac{1}{2}.AC.BC = \dfrac{1}{2}.4.2 = 4\)
Cho các số phức z thỏa mãn |z|= 2 và điểm A trong hình vẽ là điểm biểu diễn của z. Biết rằng trong hình vẽ, điểm biểu diễn số phức \(w = \dfrac{{ - 4}}{z}\) là một trong bốn điểm M, N, P, Q
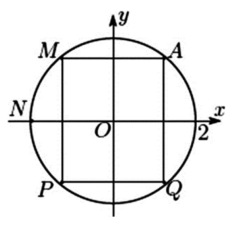
Khi đó điểm biểu diễn của số phức w là
Đặt \(z = x + yi\) \( = > {x^2} + {y^2} = 4 = > A\left( {x;y} \right)\)
Xét \(w = \dfrac{{ - 4}}{z} = \dfrac{{ - \left( {{x^2} + {y^2}} \right)}}{{x + yi}}\) \( = \dfrac{{ - \left( {x+yi} \right)\left( {x - yi} \right)}}{{\left( {x + yi} \right)}} = - x + yi\)
Điểm biểu diễn số phức w đối xứng A qua Oy
=> Điểm M.
Biết rằng tập hợp điểm biểu diễn các số phức \(z\) thỏa mãn \(\left| {\left( {1 + i} \right)z + 5 - i} \right| = 1\) là đường tròn tâm \(I\left( {a;b} \right)\). Tính \(a + b.\)
Đáp án
Đáp án
Bước 1: Chia cả 2 vế của phương trình ban đầu cho $\left| {{1+i}} \right|$
Thay vào giả thiết ta có:
$\left| {\left( {1 + i} \right)z + 5 - i} \right| = 1$
\(\begin{array}{l} \Leftrightarrow \dfrac{{\left| {\left( {1 + i} \right)z + 5 - i} \right|}}{{\left| {1 + i} \right|}} = \dfrac{1}{{\left| {1 + i} \right|}}\\ \Leftrightarrow \left| {\dfrac{{\left( {1 + i} \right)z + 5 - i}}{{1 + i}}} \right| = \dfrac{1}{{\left| {1 + i} \right|}}\end{array}\)
\(\begin{array}{l}\Leftrightarrow \left| {z + \dfrac{{5 - i}}{{1 + i}}} \right| = \dfrac{1}{{\left| {1 + i} \right|}}\\ \Leftrightarrow \left| {z + 2 - 3i} \right| = \dfrac{1}{{\sqrt 2 }} = \dfrac{{\sqrt 2 }}{2}\\ \Leftrightarrow \left| {z - \left( { - 2 + 3i} \right)} \right| = \dfrac{{\sqrt 2 }}{2}\end{array}\)
Bước 2: Tìm tâm và bán kính của đường tròn
Suy ra tập hợp các điểm biểu diễn số phức \(z\) là đường tròn tâm \(I\left( { - 2;3} \right) \Rightarrow \left\{ \begin{array}{l}a = - 2\\b = 3\end{array} \right.\).
Vậy \(a + b = - 2 + 3 = 1\).
Cho số phức \(z\) thỏa mãn \(\left| {z + i} \right| = 1\). Biết rằng tập hợp các điểm biểu diễn số phức \(w = \left( {3 + 4i} \right)z + 2 + i\) là một đường tròn tâm \(I\), điểm \(I\) có tọa độ là $I(a;b)$, tính $a-b$
Đáp án: $a-b$
Đáp án: $a-b$
Bước 1: Biểu diễn z theo w.
\(w=\left( 3+4i \right)z+2+i\Leftrightarrow \left( 3+4i \right)z=w-2-i\Leftrightarrow z=\dfrac{w-2-i}{3+4i}\)
Bước 2: Biến đổi phương trình ban đầu thành dạng \(\left| w-\left( a+bi \right) \right|=R\)
Theo bài ra ta có:
\(\begin{array}{l}\left| {z + i} \right| = 1 \Leftrightarrow \left| {\dfrac{{w - 2 - i}}{{3 + 4i}} + i} \right| = 1 \Leftrightarrow \left| {\dfrac{{w - 2 - i + 3i - 4}}{{3 + 4i}}} \right| = 1\\ \Leftrightarrow \dfrac{{\left| {w - 6 + 2i} \right|}}{{\left| {3 + 4i} \right|}} = 1 \Leftrightarrow \left| {w - \left( {6 - 2i} \right)} \right| = 5\end{array}\)
=> Tập hợp các điểm biểu diễn số phức \(w\) là đường tròn tâm \(I\left( 6;-2 \right)\) bán kính \(R=5\).
Vậy $a-b=8$
Trong mặt phẳng tọa độ, tập hợp các điểm M biểu diễn của số phức z thỏa mãn\(\left| {z + 1 + 3i} \right| = \left| {z - 2 - i} \right|\) là phương trình đường thẳng có dạng \(ax+by+c=0\). Khi đó tỉ số \(\dfrac{a}{b}\) bằng:
Đáp án:
Đáp án:
Bước 1:
Đặt \(z = a + bi\,\,\left( {a,\,\,b \in \mathbb{R}} \right).\)
Bước 2: Biến đổi rút ra mối quan hệ giữa \(a,\,\,b\) và suy ra quỹ tích các điểm biểu diễn số phức \(z\).
Theo bài ra ta có:
\(\begin{array}{l}\,\,\,\,\,\,\,\left| {z + 1 + 3i} \right| = \left| {z - 2 - i} \right|\\ \Leftrightarrow \left| {a + bi + 1 + 3i} \right| = \left| {a + bi - 2 - i} \right|\\ \Leftrightarrow {\left( {a + 1} \right)^2} + {\left( {b + 3} \right)^2} = {\left( {a - 2} \right)^2} + {\left( {b - 1} \right)^2}\\ \Leftrightarrow {a^2} + 2a + 1 + {b^2} + 6b + 9 = {a^2} - 4a + 4 + {b^2} - 2b + 1\\ \Leftrightarrow 6a + 8b + 5 = 0\end{array}\)
Suy ra tập hợp các điểm \(M\) biểu diễn số phức \(z\) là đường thẳng \(6x + 8y + 5 = 0\).
Vậy \(\dfrac{a}{b} = \dfrac{6}{8} = \dfrac{3}{4}\).
Trong mặt phẳng phức, tập hợp các điểm biểu diễn các số phức z thỏa mãn \(z.\bar z = 1\) là đường tròn có bán kính là:
Đáp án:
Đáp án:
Gọi \(z = x + yi\left( {x;y \in R} \right)\) khi đó \(\overline z = x - yi\)
Ta có: \(z.\overline z = 1 \Leftrightarrow \left( {x + yi} \right)\left( {x - yi} \right) = 1\)\( \Leftrightarrow {x^2} - {\left( {yi} \right)^2} = 1\)\( \Leftrightarrow {x^2} + {y^2} = 1\)
Vậy tập hợp điểm biểu diễn số phức \(z\) là một đường tròn có bán kính bằng 1.
Trên mặt phẳng tọa độ, cho \(M(2;3)\) là điểm biểu diễn của số phức \(z\). Phần thực của \(z\) bằng
Ta có \(M(2;3)\) là điểm biểu diễn của số phức \(z \Rightarrow z = 2 + 3i\). Vậy phần thực của \(z\) bằng 2

