Tính diện tích tứ giác \(ABCD.\)
Từ câu trước ta có tứ giác $ABCD$ là hình chữ nhật.
Hình chữ nhật \(ABCD\) có \(AB = 4;\,AD = 5\) nên diện tích \(ABCD\) bằng \(4.5 = 20 (dvdt).\)
Tứ giác \(ABCD\) là hình gì?
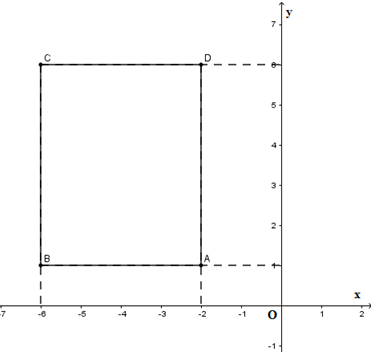
Vẽ các điểm \(A\left( { - 2;1} \right),B\left( { - 6;1} \right),C\left( { - 6;6} \right)\) và \(D\left( { - 2;6} \right)\) trên cùng mặt phẳng tọa độ.
Ta thấy \(ABCD\) là hình chữ nhật.
Tứ giác \(ABCD\) là hình gì?

Vẽ các điểm \(A\left( { - 2;1} \right),B\left( { - 6;1} \right),C\left( { - 6;6} \right)\) và \(D\left( { - 2;6} \right)\) trên cùng mặt phẳng tọa độ.
Ta thấy \(ABCD\) là hình chữ nhật.
Tứ giác \(ABCD\) là hình gì?

Vẽ các điểm \(A\left( { - 2;1} \right),B\left( { - 6;1} \right),C\left( { - 6;6} \right)\) và \(D\left( { - 2;6} \right)\) trên cùng mặt phẳng tọa độ.
Ta thấy \(ABCD\) là hình chữ nhật.
Trên mặt phẳng tọa độ $Oxy,$ vẽ các điểm \(A\left( { - 2;1} \right),B\left( { - 6;1} \right),C\left( { - 6;6} \right)\) và \(D\left( { - 2;6} \right)\)
Tứ giác \(ABCD\) là hình gì?

Vẽ các điểm \(A\left( { - 2;1} \right),B\left( { - 6;1} \right),C\left( { - 6;6} \right)\) và \(D\left( { - 2;6} \right)\) trên cùng mặt phẳng tọa độ.
Ta thấy \(ABCD\) là hình chữ nhật.
Trên mặt phẳng tọa độ $Oxy,$ vẽ các điểm \(A\left( { - 2;1} \right),B\left( { - 6;1} \right),C\left( { - 6;6} \right)\) và \(D\left( { - 2;6} \right)\)
Tính diện tích tứ giác \(ABCD.\)
Từ câu trước ta có tứ giác $ABCD$ là hình chữ nhật.
Hình chữ nhật \(ABCD\) có \(AB = 4;\,AD = 5\) nên diện tích \(ABCD\) bằng \(4.5 = 20 (dvdt).\)
Cho hàm số giá trị tuyết đối \(y = f(x) = \left| {3x - 1} \right|\)
Tính $f\left( { - \dfrac{1}{4}} \right) - f\left( {\dfrac{1}{4}} \right)$
Ta có \(f\left( { - \dfrac{1}{4}} \right) = \left| {3.\dfrac{{ - 1}}{4} - 1} \right| = \left| {\dfrac{{ - 7}}{4}} \right| = \dfrac{7}{4}\) ; \(f\left( {\dfrac{1}{4}} \right) = \left| {3.\dfrac{1}{4} - 1} \right| = \left| { - \dfrac{1}{4}} \right| = \dfrac{1}{4}\)
Suy ra \(f\left( { - \dfrac{1}{4}} \right) - f\left( {\dfrac{1}{4}} \right) = \dfrac{7}{4} - \dfrac{1}{4} = \dfrac{3}{2}.\)
Cho hàm số giá trị tuyết đối \(y = f(x) = \left| {3x - 1} \right|\)
Tìm $x$, biết \(f\left( x \right) = 10.\)
Từ \(f\left( x \right) = 10\) ta có \(\left| {3x - 1} \right| = 10\)

Vậy \(x = \dfrac{{11}}{3}\) hoặc \(x = - 3.\)
Cho hàm số \(y = 3{x^2} + 1\). So sánh \(f\left( x \right)\) và \(f\left( { - x} \right)\).
Ta có \(f\left( x \right) = 3{x^2} + 1\) và \(f\left( { - x} \right) = 3{\left( { - x} \right)^2} + 1 = 3{x^2} + 1\)
Nên \(f\left( x \right) = f\left( { - x} \right)\)
Cho hàm số xác định bởi \(y = f\left( x \right) = 40x + 20\). Với giá trị nào của \(x\) thì \(f\left( x \right) = 300?\)
Từ \(f\left( x \right) = 300\) ta có \(40x + 20 = 300\)
\(40x = 300 - 20 \Rightarrow 40x = 280\)\( \Rightarrow x = 7\)
Vậy \(x = 7\) thì \(f\left( x \right) = 300.\)
Hãy cho biết vị trí của các điểm có hoành độ lớn hơn \(0\) nhỏ hơn \(1\) và có tung độ lớn hơn \(0\) nhỏ hơn \(4.\)
Vẽ bốn đường thẳng \(x = 0;x = 1;y = 0;y = 4\) trên cùng mặt phẳng tọa độ.
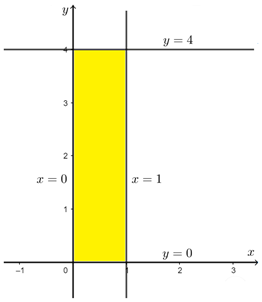
Dựa vào hình vẽ, vị trí các điểm có hoành độ lớn hơn \(0\) nhỏ hơn \(1\) và có tung độ lớn hơn \(0\) nhỏ hơn \(4\) nằm trong hình chữ nhật được giới hạn bởi bốn đường thẳng \(x = 0;x = 1;y = 0;y = 4\) (phần bôi vàng), không tính các điểm thuộc bốn đường thẳng trên.

