Đề thi thử THPTQG môn Toán THPT Kim Liên Hà Nội lần 3

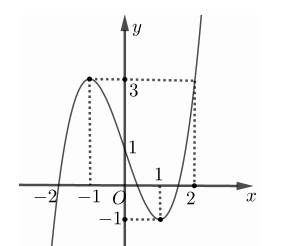
Cho hàm số \(y = f\left( x \right)\) xác định, liên tục trên đoạn \(\left[ { - 2;2} \right]\) và có đồ thị là đường cong trong hình vẽ bên. Hàm số \(f\left( x \right)\) đạt cực tiểu tại điểm nào dưới đây?

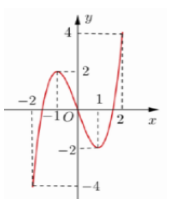
Trong không gian \(Oxyz,\) mặt cầu \(\left( S \right):{x^2} + {y^2} + {z^2} - 8x + 4y + 2z - 4 = 0\) có bán kính \(R\) là

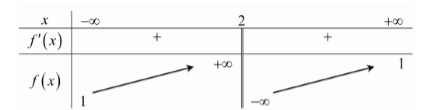
Cho hàm số \(y = f\left( x \right)\) liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau. Chọn khẳng định đúng?

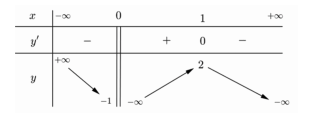
Cho \(n\) là số nguyên dương và \(C_n^5 = 792.\) Tính \(A_n^5.\)

Một khối trụ có bán kính đáy bằng \(2\), chiều cao bằng \(3\). Tính thể tích \(V\) của khối trụ.

Trong không gian \(Oxyz,\) mặt phẳng \(\left( P \right):x - 2y + z - 5 = 0\). Điểm nào dưới đây thuộc \(\left( P \right)?\)

Khối hộp chữ nhật có các kích thước lần lượt là \(a,2a,3a\) có thể tích bằng

Tìm nguyên hàm của hàm số \(f\left( x \right) = \cos 5x\)

Cho cấp số nhân \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1} = \dfrac{1}{2}\) và công bội \(q = 3\). Tính \({u_5}\).

Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:

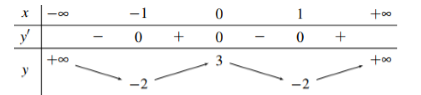
Hàm số đã cho đồng biến trên khoảng nào dưới đây?

Trong không gian \(Oxyz\), cho điểm \(M\) thỏa mãn hệ thức \(\overrightarrow {OM}  = 2\overrightarrow i  + \overrightarrow j \). Tọa độ của điểm \(M\) là

Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 2;2} \right]\) và có đồ thị bên. Gọi \(M,m\) lần lượt là giá trị lớn nhất và nhỏ nhất của đồ thị hàm số đã cho trên đoạn \(\left[ { - 2;2} \right]\). Giá trị của \(M + m\) bằng

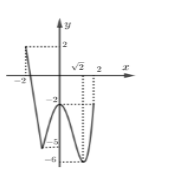
Cho số phức \(z = {\left( {2i - 1} \right)^2} - {\left( {3 + i} \right)^2}\). Tổng phần thực và phần ảo và phần ảo của \(z\) là

Cho số phức \(z = a + bi\,\,\left( {a;b \in \mathbb{R}} \right)\) thỏa mãn \(3z - \left( {4 + 5i} \right)\overline z  =  - 17 + 11i\). Tính \(ab.\)

Trong không gian \(Oxyz\), véc tơ nào sau đây là một véc tơ chỉ phương của đường thẳng \(\Delta :\dfrac{{x - 1}}{1} = \dfrac{{y + 2}}{{ - 1}} = \dfrac{z}{2}\)?

Tìm các số thực \(x,y\) thỏa mãn \(\left( {3 - 2i} \right)\left( {x - yi} \right) - 4\left( {1 - i} \right) = \left( {2 + i} \right)\left( {x + yi} \right)\)

Bảng biến thiên sau đây là của hàm số nào?

Cho hình hộp \(ABCD.A'B'C'D'\). Gọi \({V_1};{V_2}\) lần lượt là thể tích của khối tứ diện \(ACB'D'\) và khối hộp \(ABCD.A'B'C'D'.\) Tỉ số \(\dfrac{{{V_1}}}{{{V_2}}}\) bằng

Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có \(AB = a,AD = 2a,AA' = 3a\). Thể tích khối cầu ngoại tiếp hình hộp chữ nhật \(ABCD.A'B'C'D'\) là

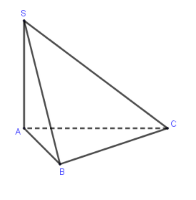
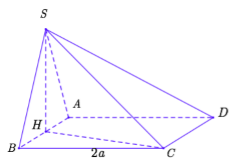
Cho hình chóp tam giác đều \(S.ABC\) có \(SA = 2a,AB = 3a.\) Gọi \(M\) là trung điểm \(SC.\) Tính khoảng cách từ \(M\)  đến mặt phẳng  \(\left( {SAB} \right)\).

Cho \(\log 3 = m;\ln 3 = n\). Hãy biểu diễn \(\ln 30\) theo \(m\) và \(n\).

Cho số phức \(z = \left( {m + 3} \right) + \left( {{m^2} - m - 6} \right)i\) với \(m \in \mathbb{R}.\) Gọi \(\left( P \right)\) là tập hợp điểm biểu diễn số phức \(z\) trong mặt phẳng tọa độ. Diện tích hình phẳng giới hạn bởi \(\left( P \right)\) và trục hoành bằng

Trong không gian tọa độ \(Oxyz\), cho hình thang cân \(ABCD\) có các cạnh đáy lần lượt là \(AB,CD\). Biết \(A\left( {3;1; - 2} \right)\), \(B\left( { - 1;3;2} \right),C\left( { - 6;3;6} \right)\) và \(D\left( {a;b;c} \right)\) với \(a,b,c \in \mathbb{R}\). Tính \(T = a + b + c\).

Biết \(\int\limits_2^{e + 1} {\dfrac{{\ln \left( {x - 1} \right)}}{{{{\left( {x - 1} \right)}^2}}}dx = a + b{e^{ - 1}}} \) với \(a,b \in \mathbb{Z}.\) Chọn khẳng định đúng trong các khẳng định sau:

Số lượng loại vi khuẩn \(A\) trong một phòng thí nghiệm được tính theo công thức \(s\left( t \right) = s\left( 0 \right){.2^t}\), trong đó \(s\left( 0 \right)\) là số lượng vi khuẩn \(A\) lúc ban đầu, \(s\left( t \right)\) là số lượng vi khuẩn \(A\) có sau \(t\) phút. Biết sau \(3\) phút thì số vi khuẩn \(A\) là \(625\) nghìn con. Hỏi sau bao lâu kể từ lúc ban đầu, số lượng vi khuẩn \(A\) là \(20\) triệu con.

Tìm tập nghiệm S của bất phương trình \({\log _3}\left( {2x + 3} \right) < {\log _3}\left( {1 - x} \right)\)

Cho khối chóp \(S.ABC\) có đáy \(ABC\) là tam giác cân tại \(A\), biết \(SA \bot \left( {ABC} \right)\), \(BC = 2a,\widehat {BAC} = {120^0}\), góc giữa mặt phẳng \(\left( {SBC} \right)\) và \(\left( {ABC} \right)\) bằng \({45^0}\). Tính thể tích khối chóp \(S.ABC\).

Nếu \(\log 3 = a\) thì \(\log 9000\) bằng

Trong không gian tọa độ \(Oxyz\), phương trình đường thẳng đi qua \(A\left( {1;2;4} \right)\), song song với \(\left( P \right)\): \(2x + y + z - 4 = 0\) và cắt đường thẳng \(d:\dfrac{{x - 2}}{3} = \dfrac{{y - 2}}{1} = \dfrac{{z - 2}}{5}\) có phương trình:

Cho \(\int\limits_0^1 {\left( {1 + 3x} \right)f'\left( x \right)dx}  = 2019;\) \(4f\left( 1 \right) - f\left( 0 \right) = 2020.\) Tính \(\int\limits_0^{\frac{1}{3}} {f\left( {3x} \right)dx.} \)

Cho hàm số \(y = {x^3} - 6mx + 4\) có đồ thị \(\left( {{C_m}} \right)\). Gọi \({m_0}\) là giá trị của \(m\) để đường thẳng đi qua điểm cực đại, điểm cực tiểu của \(\left( {{C_m}} \right)\) cắt đường tròn tâm \(I\left( {1;0} \right)\), bán kính \(\sqrt 2 \) tại hai điểm phân biệt \(A,B\) sao cho tam giác \(IAB\) có diện tích lớn nhất. Chọn khẳng định đúng?

Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ.

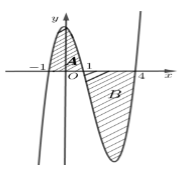
Diện tích hai phần \(A\) và \(B\) lần lượt là \(\dfrac{{16}}{3}\) và \(\dfrac{{63}}{4}.\) Tính \(\int\limits_{ - 1}^{\dfrac{3}{2}} {f\left( {2x + 1} \right)dx} \).

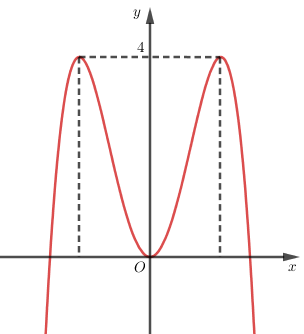
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình bên. Tìm tất cả các giá trị thực của tham số \(m\) để phương trình \(f\left( x \right) = {\log _2}m\) có hai nghiệm phân biệt.

Cho hàm số \(f\left( x \right) = {x^2}\left( {x - 1} \right){e^{3x}}\) có một nguyên hàm là hàm số \(F\left( x \right).\) Số cực trị của hàm số \(F\left( x \right)\) là

Trong không gian \(Oxyz\), cho điểm \(M\left( {1;2;3} \right)\). Gọi \(A,B,C\) lần lượt là hình chiếu của \(M\) trên các trục \(Ox,Oy,Oz\). Viết phương trình mặt phẳng \(\left( {ABC} \right)\).

Biết \(\int\limits_0^{\dfrac{\pi }{2}} {\dfrac{{3\sin x + \cos x}}{{2\sin x + 3\cos x}}dx =  - \dfrac{7}{{13}}\ln 2 + b\ln 3 + c\pi \,\,\left( {b,c \in \mathbb{Q}} \right).} \) Tính \(\dfrac{b}{c}.\)

Tìm tất cả các giá trị của tham số \(m\) để hàm số \(y = \dfrac{1}{3}{x^3} - \left( {2m - 1} \right){x^2} + \left( {{m^2} - m + 7} \right)x + m - 5\) có hai điểm cực trị là độ dài hai cạnh góc vuông của một tam giác vuông có cạnh huyền bằng \(\sqrt {74} \).

Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh bằng \(2a.\)  Tam giác \(SAB\) cân tại \(S\) và nằm trong mặt phẳng vuông góc với mặt đáy. Biết thể tích khối chóp \(S.ABCD\) bằng \(\dfrac{{4{a^3}}}{3}\) . Gọi \(\alpha \)  là góc giữa \(SC\) và mặt đáy, tính \(\tan \alpha .\)

Tổng bình phương các nghiệm của phương trình \({5^{3x - 2}} = {\left( {\dfrac{1}{5}} \right)^{ - {x^2}}}\) bằng

Tính tổng tất cả các nghiệm thực của phương trình \({\log _{\sqrt 3 }}\left( {x - 2} \right) + {\log _3}{\left( {x - 4} \right)^2} = 0.\)

Cho hai số phức \({z_1},{z_2}\) thỏa mãn \(\left| {{z_1}} \right| = 6,\left| {{z_2}} \right| = 2\). Gọi \(M,N\) lần lượt là các điểm biểu diễn của số phức \({z_1}\) và số phức \(i{z_2}\). Biết \(\widehat {MON} = {60^0}\). Tính \(T = \left| {z_1^2 + 9z_2^2} \right|\).

Gọi S là tập các số tự nhiên gồm 9 chữ số được lập từ tập \(X = \left\{ {6;7;8} \right\},\) trong đó chữ số 6 xuất hiện 2 lần, chữ số 7 xuất hiện 3 lần, chữ số 8 xuất hiện 4 lần. Chọn ngẫu nhiên một số từ tập S; tính xác suất để số được chọn là số không có chữ số 7 đứng giữa hai chữ số 6.

Trong không gian \(Oxyz\), cho hình lăng trụ tam giác đều \(ABC.A'B'C'\) có \(A'\left( {\sqrt 3 ; - 1;1} \right)\), hai đỉnh \(B,C\) thuộc trục \(Oz\) và \(AA' = 1\) (\(C\) không trùng với \(O\)). Biết véc tơ \(\overrightarrow u  = \left( {a;b;2} \right)\) với \(a,b \in \mathbb{R}\) là một véc tơ chỉ phương của đường thẳng \(A'C\). Tính \(T = {a^2} + {b^2}\).

Cho bất phương trình \(\sqrt[3]{{{x^4} + {x^2} + m}} - \sqrt[3]{{2{x^2} + 1}} + {x^2}\left( {{x^2} - 1} \right) > 1 - m\). Tìm tất cả các giá trị thực của tham số \(m\) để bất phương trình nghiệm đúng với mọi \(x > 1.\)

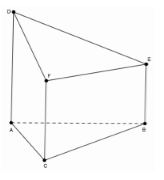
Cho đa diện \(ABCDEF\) có \(AD,BE,CF\) đôi một song song. \(AD \bot \left( {ABC} \right)\), \(AD + BE + CF = 5\), diện tích tam giác \(ABC\) bằng \(10\). Thể tích đa diện \(ABCDEF\) bằng

Trong không gian \(Oxyz,\) cho hai điểm \(M\left( { - 2; - 2;1} \right),A\left( {1;2; - 3} \right)\) và đường thẳng \(d:\dfrac{{x + 1}}{2} = \dfrac{{y - 5}}{2} = \dfrac{z}{{ - 1}}.\) Gọi \(\Delta \) là đường thẳng qua \(M,\) vuông góc với đường thẳng \(d,\) đồng thời cách điểm \(A\) một khoảng bé nhất. Khoảng cách bé nhất đó là

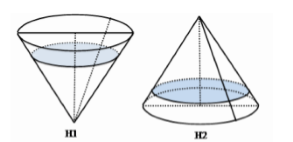
Một khối đồ chơi có dạng khối nón, chiều cao bằng \(20cm\), trong đó có chứa một lượng nước. Nếu đặt khối đồ chơi theo hình H1 thì chiều cao của lượng nước bằng \(\dfrac{2}{3}\) chiều cao của khối nón. Hỏi nếu đặt khối đồ chơi theo hình H2 thì chiều cao \(h\) của lượng nước trong khối đó gần với giá trị nào sau đây?

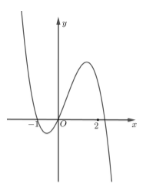
Cho hàm số \(f\left( x \right) = a{x^4} + b{x^3} + c{x^2} + dx + e,\) với \(a,b,c,d,e \in \mathbb{R}.\) Hàm số \(y = f'\left( x \right)\) có đồ thị như hình vẽ. Trong các khẳng định sau, khẳng định nào đúng?

Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ dưới đây. Gọi \(S\) là tập hợp tất cả các giá trị của tham số \(m\) để phương trình \(f\left( {3 - \sqrt {4 - {x^2}} } \right) = m\) có hai nghiệm phân biệt thuộc đoạn \(\left[ { - \sqrt 2 ;\sqrt 3 } \right]\). Tìm tập \(S\).

Cho hàm số \(y = f\left( x \right) = {2^{2019}}{x^3} + {3.2^{2018}}{x^2} - 2018\) có đồ thị cắt trục hoành tại ba điểm phân biệt có hoành độ \({x_1};{x_2};{x_3}\). Tính giá trị biểu thức \(P = \dfrac{1}{{f'\left( {{x_1}} \right)}} + \dfrac{1}{{f'\left( {{x_2}} \right)}} + \dfrac{1}{{f'\left( {{x_3}} \right)}}.\)

Cho biểu đồ GDP của Ma-lai-xi-a và Phi-lip-pin qua các năm

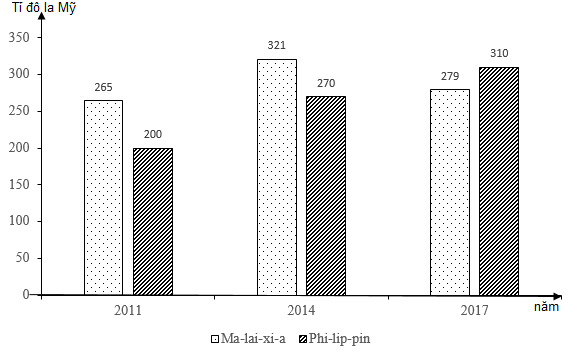
(Nguồn: Niến giám thống kê Việt Nam 2017, NXB Thống kê, 2019)

Biểu đồ thể hiện nội dung nào sau đây?

Năng suất lúa cả năm của nước ta có xu hướng tăng, chủ yếu do

Nội thương của nước ta hiện nay

Phát biểu nào sau đây không đúng về tự nhiên của Đông Nam Á lục địa?

Xu hướng thay đổi lãnh thổ công nghiệp của Hoa Kì trong những năm gần đây là

Mục đích chính của việc đẩy mạnh đánh bắt xa bờ ở nước ta là

Căn cứ vào Atlat Địa lí Việt Nam trang 15, hãy cho biết tỉ trọng dân thành thị và nông thôn năm 2007 lần lượt là (đơn vị: %) 

Cho bảng số liệu:

SẢN LƯỢNG MỘT SỐ SẢN PHẨM CÔNG NGHIỆP CỦA NƯỚC TA GIAI ĐOẠN 2010 – 2018

(Nguồn: Niên giám thống kê Việt Nam 2018, NXB Thống kê, 2019)

Theo bảng số liệu trên, để thể hiện tốc độ tăng trưởng sản lượng một số sản phẩm công nghiệp của nước ta giai đoạn 2010 – 2018, dạng biểu đồ nào sau đây là thích hợp nhất?

Để nâng cao chất lượng và hạ giá thành sản phẩm, công nghiệp nước ta cần phải

Nhận định nào sau đây đúng về dân cư nước ta hiện nay?

Ngành nào sau đây đặc trưng cho nông nghiệp ở khu vực Đông Nam Á?

Nội dung nào sau đây không nằm trong các mặt tự do lưu thông của thị trường chung châu Âu?

Ở nước ta, rừng phòng hộ bao gồm

Sông ngòi của nước ta có chế độ nước thay đổi theo mùa, do

Căn cứ vào Atlat Địa lí Việt Nam trang 19, hãy xác định tỉnh có diện tích cây công nghiệp lâu năm lớn nhất ở vùng Bắc Trung Bộ?

Cho bảng số liệu

Mật độ dân số một số vùng nước ta, năm 2006.

(Đơn vị: người/km)

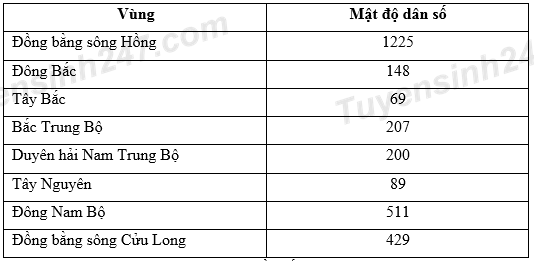
(Nguồn số liệu theo Bài 16 - SGK trang 69 - NXB giáo dục Việt Nam)

Để thể hiện mật độ dân số một số vùng nước ta năm 2006 theo bảng số liệu, biểu đồ nào sau đây là thích hợp nhất ?

Khó khăn lớn nhất đối với việc phát triển cây công nghiệp lâu năm hiện nay ở nước ta là

Điều kiện thuận lợi nhất về tự nhiên để xây dựng các cảng biển ở nước ta là:

Thuận lợi chủ yếu đối với phát triển cây công nghiệp cận nhiệt ở Trung du và miền núi Bắc Bộ là

Đồng bằng sông Hồng không có thế mạnh về

Đại bộ phận lãnh thổ của Liên bang Nga nằm trong vành đai khí hậu

Yếu tố vị trí địa lí và lãnh thổ giúp Nhật Bản phát triển mạnh loại hình giao thông vận tải nào sau đây?

Đất ở đồng bằng ven biển miền Trung nước ta thường nghèo, nhiều cát do

Căn cứ vào Atlat Địa lí Việt Nam trang 19, hãy xác định tỉnh có diện tích cây công nghiệp lâu năm lớn nhất ở vùng Bắc Trung Bộ?

Cho biểu đồ:

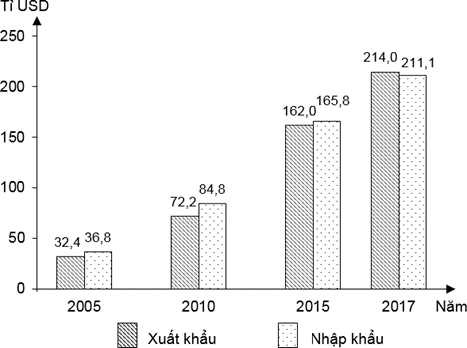
TÌNH HÌNH XUẤT, NHẬP KHẨU CỦA VIỆT NAM, GIAI ĐOẠN 2005 - 2017

(Nguồn số liệu theo Niên giám thống kê Việt Nam 2018, NXB Thống kê, 2019)

Theo biểu đồ, nhận xét nào sau đây đúng về xuất, nhập khẩu của nước ta giai đoạn 2005 - 2017?

Trong những năm qua, sản lượng lương thực của nước ta tăng lên chủ yếu là do

Hạn chế lớn nhất trong phát triển công nghiệp Nhật Bản là

Vấn đề dân cư mà Nhà nước Liên bang Nga quan tâm nhất hiện nay là

Ở Việt Nam, vùng sẽ chịu ảnh hưởng nặng nề nhất của biến đổi khí hậu do nước biển dâng là

Phát biểu nào sau đây không đúng với khí hậu phần lãnh thổ phía Bắc nước ta (từ dãy Bạch Mã trở ra)?

Căn cứ và Atlat Địa lí Việt Nam trang 14, cho biết sông Đồng Nai bắt nguồn từ cao nguyên nào sau đây?

Cho bảng số liệu:

LAO ĐỘNG PHÂN THEO KHU VỰC KINH TẾ NƯỚC TA, GIAI ĐOẠN 2009 - 2019

(Đơn vị: Nghìn người)

(Nguồn: Niên giám thống kê 2019, NXB Thống kê, 2020)

Theo bảng số liệu, để thể hiện tốc độ tăng trưởng lao động phân theo khu vực kinh tế nước ta giai đoạn 2009 - 2019, dạng biểu đồ nào sau đây là thích hợp nhất?

Ý nào dưới đây không đúng với sự chuyển dịch cơ cấu ngành công nghiệp nước ta hiện nay?

Ở nước ta, trong các ngành giao thông vận tải sau, ngành nào có ý nghĩa quan trọng đối với vận tải quốc tế?

Tây Nguyên hiện nay phát triển mạnh

Vấn đề quan trọng trong phát triển nông nghiệp theo chiều sâu ở Đông Nam Bộ là

Ý nào sau đây không phải là một trong những đặc điểm về vị trí địa lí của Hoa Kì?

Ngành công nghiệp nào sau đây phát triển mạnh ở Trung Quốc nhờ lực lượng lao động dồi dào?

Biện pháp nào sau đây không phải là biện pháp để hạn chế thiệt hại của lũ quét?

Điểm khác chủ yếu của Đồng bằng sông Hồng so với Đồng bằng sông Cửu Long là ở đồng bằng này có

Căn cứ vào Atlat Địa lí Việt Nam trang 15, nhận xét nào sau đây không đúng về dân số phân theo thành thị và nông thôn ở nước ta?

Cho biểu đồ về tình hình sinh và tử của nước ta giai đoạn 1999 – 2019

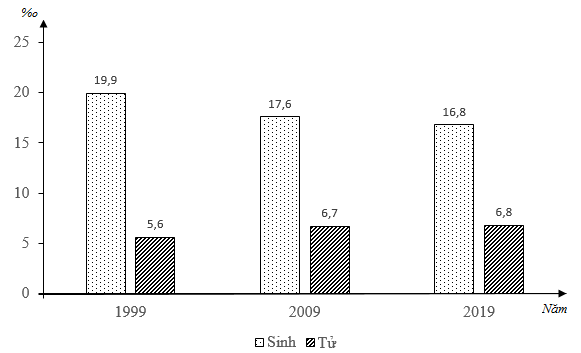
(Nguồn: Niên giám thống kê Việt Nam 2019, Nhà xuất bản thống kê 2019)

Biểu đồ trên thể hiện nội dung nào sau đây?

Nhận định nào sau đây đúng về dân cư – xã hội Châu Phi?

Quốc gia nào hiện nay đầu tư vào khu vực Mĩ latinh nhiều nhất?

Đâu là đặc điểm của bão ở nước ta?

Nguyên nhân khiến thiên nhiên nước ta xanh tốt khác với các nước có cùng vĩ độ ở Tây Nam Á và Bắc Phi là do

Căn cứ vào Atlat Địa lí Việt Nam trang 16, cho biết nhận xét nào sau đây đúng về phân bố các dân tộc Việt Nam?

Cho bảng số liệu:

DÂN SỐ VÀ TỈ LỆ GIA TĂNG DÂN SỐ TỰ NHIÊN CỦA NƯỚC TA QUA CÁC NĂM

 (Nguồn: Tổng điều tra dân số Việt Nam năm 2019)

Theo bảng số liệu, để thể hiện dân số và tỉ lệ gia tăng dân số tự nhiên của nước ta qua các năm, dạng biểu đồ nào sau đây là thích hợp nhất?

Nhân tố quan trọng nhất ảnh hưởng đến sự phát triển và phân bố các khu công nghiệp của nước ta hiện nay là

Thế mạnh nông nghiệp nhiệt đới ở trung du và miền núi nước ta là

Ở Trung du và miền núi Bắc Bộ, khu vực Tây Bắc có thể mạnh nổi bật hơn Đông Bắc về

Cơ cấu công nghiệp của Bắc Trung Bộ chưa thật định hình là do những hạn chế về