Câu hỏi:
2 năm trước
Cho hình hộp \(ABCD.A'B'C'D'\). Gọi \({V_1};{V_2}\) lần lượt là thể tích của khối tứ diện \(ACB'D'\) và khối hộp \(ABCD.A'B'C'D'.\) Tỉ số \(\dfrac{{{V_1}}}{{{V_2}}}\) bằng
Trả lời bởi giáo viên
Đáp án đúng: a
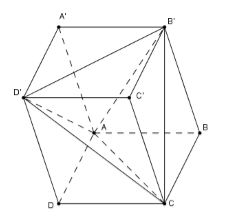
Ta thấy \({V_1} = {V_{ABCD.A'B'C'D'}} = h.{S_{ABCD}}\) với \(h = d\left( {A',\left( {ABCD} \right)} \right)\)
+) \({V_{D'.ADC}} = \dfrac{1}{3}d\left( {D',\left( {ADC} \right)} \right).{S_{\Delta ADC}} = \dfrac{1}{3}.h.\dfrac{1}{2}{S_{ABCD}} = \dfrac{1}{6}{V_1}\)
Tương tự ta có \({V_{C.D'C'B'}} = {V_{B'.ABC}} = {V_{A.A'B'D'}} = {V_{D'.ADC}} = \dfrac{1}{6}{V_1}\)
Lại có \({V_{C.D'C'B'}} + {V_{B'.ABC}} + {V_{A.A'B'D'}} + {V_{D'.ADC}} + {V_{ACB'D'}} = {V_{ABCD.A'B'C'D'}}\)
\( \Leftrightarrow {V_2} = {V_{ACB'D'}} = {V_1} - 4.\dfrac{1}{6}{V_1} = \dfrac{{{V_1}}}{3} \Leftrightarrow \dfrac{{{V_1}}}{{{V_2}}} = \dfrac{1}{3}\).
Hướng dẫn giải:
Thể tích khối chóp \(V = \dfrac{1}{3}S.h\).
Thể tích khối hộp \(V = S.h\).
Câu hỏi khác
- Đề thi thử THPTQG môn Toán Chuyên ĐH Vinh Nghệ An lần 3 Toán 12 có lời giải chi tiết
- Đề thi thử THPTQG - Đề số 2 Toán 12 có lời giải chi tiết
- Đề thi thử THPTQG - Đề số 1 Toán 12 có lời giải chi tiết
- Đề tập huấn thi THPTQG Sở Giáo Dục và Đào Tạo Bắc Ninh 2019 Toán 12 có lời giải chi tiết
- Đề thi thử THPTQG - Đề số 4 Toán 12 có lời giải chi tiết
