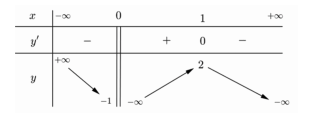
Cho hàm số \(y = f\left( x \right)\) liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau. Chọn khẳng định đúng?

Hướng dẫn giải:

Sử dụng định nghĩa các đường tiệm cận của đồ thị hàm số:

- Tiệm cận đứng: Đường thẳng \(x = {x_0}\) được gọi là tiệm cận đứng của đồ thị hàm số \(y = f\left( x \right)\) nếu nó thỏa mãn một trong 4 điều kiện sau: \(\left[ \begin{array}{l}\mathop {\lim }\limits_{x \to x_0^ + } y =  + \infty \\\mathop {\lim }\limits_{x \to x_0^ + } y =  - \infty \\\mathop {\lim }\limits_{x \to x_0^ - } y =  + \infty \\\mathop {\lim }\limits_{x \to x_0^ - } y =  - \infty \end{array} \right.\)

- Tiệm cận ngang: Đường thẳng \(y = {y_0}\) được gọi là tiệm cận ngang của đồ thị hàm số \(y = f\left( x \right)\) nếu nó thỏa mãn một trong 2 điều kiện sau: \(\left[ \begin{array}{l}\mathop {\lim }\limits_{x \to  + \infty } y = {y_0}\\\mathop {\lim }\limits_{x \to  - \infty } y = {y_0}\end{array} \right.\)