Đề thi thử THPTQG - Đề số 4

Cho hàm số $y=f(x)$ liên tục trên đoạn $\left( a;b \right)$và $f(x)>0,\forall x\in \left( a;b \right)$. Gọi D là hình phẳng giới hạn bởi đồ thị hàm số $y=f(x)$, trục hoành và 2 đường thẳng $x=a,\,\,x=b\,\,(a<b)$. Thể tích của vật thể tròn xoay khi quay D quanh Ox được tính theo công thức:

Trong không gian với hệ trục $Oxyz$, mặt phẳng đi qua điểm $A\left( {1,3, - 2} \right)$ và song song với mặt phẳng $\left( P \right):2x - y + 3z + 4 = 0$  là:

Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh bằng $1$. Tam giác $SAB$ đều và nằm trong mặt phẳng vuông góc với đáy $\left( {ABCD} \right)$. Tính khoảng cách $d$ từ $A$ đến $\left( {SCD} \right)$.

Trong không gian với hệ tọa độ $Oxyz$, cho mặt cầu $\left( S \right):{x^2} + {\left( {y - 1} \right)^2} + {\left( {z - 2} \right)^2} = 25$. Điểm nào sau đây nằm bên trong mặt cầu $\left( S \right)$.

Trong không gian $Oxyz$, cho tam giác $OAB$ với $A\left( {1;1;2} \right),\;B\left( {3; - 3;0} \right)$. Phương trình đường trung tuyến $OI$ của tam giác $OAB$ là

Cho hàm số $y=f\left( x \right)$ liên tục trên $R$ và thỏa mãn $\int\limits_{{}}^{{}}{f\left( x \right)dx}=4{{x}^{3}}-3{{x}^{2}}+2x+C$. Hàm số $f\left( x \right)$ là hàm số nào trong các hàm số sau?

Trong các phương trình sau đây, phương trình nào có nghiệm?

Giá trị của $C = \lim \dfrac{{{{\left( {2{n^2} + 1} \right)}^4}{{\left( {n + 2} \right)}^9}}}{{{n^{17}} + 1}}$ bằng:

Hình trụ có bán kính đáy $r = 2cm$ và chiều cao $h = 5cm$ có diện tích xung quanh:

Có bao nhiêu số tự nhiên có các chữ số đôi một khác nhau nhỏ hơn $1000$ được lập từ năm chữ số $0,1,2,3,4$?

Tích phân $I = \int\limits_1^2 {{x^5}} dx$ có giá trị là:

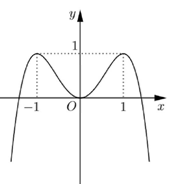
Đường cong trong hình bên là đồ thị của một trong bốn hàm số nào sau đây?

Cho hàm số $y = \dfrac{{x - 2}}{{x + 2}}$ có đồ thị $(C)$. Tìm tọa độ giao điểm $I$ của hai đường tiệm cận của đồ thị $(C)$

Cho hình lăng trụ đứng $ABC.A'B'C'$ có đáy là tam giác cân tại $A$. $AB = AC = 2a,\widehat {CAB} = {120^0}.$ Mặt phẳng $\left( {AB'C'} \right)$ tạo với đáy một góc ${60^0}$. Thể tích khối lăng trụ là:

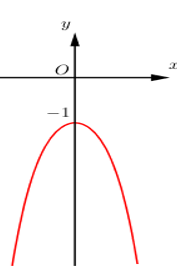
Đường cong hình bên là đồ thị hàm số nào sau đây:

Kí hiệu $a,b$ lần lượt là phần thực và phần ảo của số phức $3 - 2\sqrt 2 i$. Tìm $a,b.$

Trong không gian với hệ tọa độ $Oxyz$, cho mặt phẳng $\left( P \right):9x + 3y - 10z + 26 = 0$ và đường thẳng $d:\dfrac{{x + 1}}{2} = \dfrac{{y - 1}}{4} = \dfrac{{z - 2}}{3}$. Mệnh đề nào sau đây là đúng?

Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a$ và $SA = SB = SC = b$. Gọi $G$ là trọng tâm $\Delta ABC$. Độ dài $SG$ là:

Tìm các giá trị của tham số $m$ sao cho hàm số $y =  - {x^3} - {x^2} + mx + 1$ nghịch biến trên $R$?

Cho hàm số $y = {x^3} - 3{x^2} - 9x + m$. Viết phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số.

Cho hàm số $y = {x^3} - 3m{x^2} + 6$, giá trị nhỏ nhất của hàm số trên $\left[ {0;3} \right]$ bằng $2$ khi:

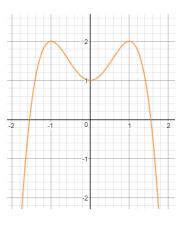
Cho hàm số $y =  - {x^4} + 2{{\rm{x}}^2} + 1$ có đồ thị như hình bên

Tìm tất cả các giá trị thực của tham số $m$ để phương trình $- {x^4} + 2{{\rm{x}}^2} + 1 = m$ có $3$ nghiệm phân biệt

Gọi $M\left( a;b \right)$ là điểm trên đồ thị hàm số $y=\dfrac{2x+1}{x+2}$ mà có khoảng cách đến đường thẳng $d:y=3x+6$ nhỏ nhất. Khi đó

Tìm $m$ để phương trình ${x^5} + {x^3} - \sqrt {1 - x}  + m = 0$ có nghiệm trên $\left( { - \infty ;1} \right]$.

Một người gửi vào ngân hàng một số tiền là 100.000.000 triệu đồng, họ định gửi theo kì hạn n năm với lãi suất là 12%/năm ; sau mỗi năm không nhận lãi mà để lãi nhập vốn cho năm kế tiếp. Tìm n nhỏ nhất để số tiền lãi nhận được lớn hơn 40.000.000 đồng?

Đặt $a = {\log _2}5$ và $b = {\log _2}6$. Hãy biểu diễn ${\log _3}90$ theo $a$ và $b$?

Tính tổng $T$ tất cả các nghiệm của phương trình ${4.9^x} - {13.6^x} + {9.4^x} = 0$.

Biết tích phân $I = \int\limits_0^1 {x{e^{2x}}dx}  = a{e^2} + b$ ($a,b$ là các số hữu tỉ). Khi đó tổng $a + b$ là:

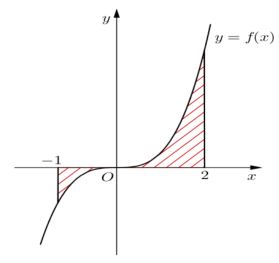
Gọi $S$ là diện tích hình phẳng $\left( H \right)$ giới hạn bởi các đường $y=f\left( x \right),~$trục hoành và hai đường thẳng $x =  - 1,x = 2$ (như hình vẽ). Đặt $a=\underset{-1}{\overset{0}{\mathop \int }}\,f\left( x \right)dx,~b=\underset{0}{\overset{2}{\mathop \int }}\,f\left( x \right)dx.$  Mệnh đề nào sau đây đúng?

Thu gọn số phức $w = {i^5} + {i^6} + {i^7} + ... + {i^{18}}$ có dạng $a + bi$. Tính tổng $S = a + b.$

Cho số phức $z$ có $|z| = 4$. Tập hợp các điểm $M$  trong mặt phẳng tọa độ $Oxy$ biểu diễn số phức $w = \bar z + 3i$  là một đường tròn. Tính bán kính đường tròn đó.

Cho hàm số $f\left( x \right)$ có đạo hàm liên tục trên R thỏa mãn $f'\left( x \right) = f\left( x \right) + {x^2}{e^x} + 1\,\,\forall x \in R$ và $f\left( 0 \right) =  - 1$. Tính $f\left( 3 \right)$.

Cho lăng trụ đứng $ABC.A'B'C'$ với $ABC$ là tam giác vuông cân tại $C$ có $AB = a$ , mặt bên $ABB'A'$ là hình vuông. Mặt phẳng qua trung điểm $I$ của $AB$ và vuông góc với $AB'$ chia khối lăng trụ thành 2 phần. Tính thể tích mỗi phần?

Cho lăng trụ $ABC.A'B'C'$ có đáy $ABC$  là tam giác đều cạnh $a$, và $A'A = A'B = A'C = a\sqrt {\dfrac{7}{{12}}}$ . Thể tích khối lăng trụ $ABC.A'B'C'$ theo $a$ là:

Một đội xây dựng cần hoàn thiện một hệ thống cột tròn của một cửa hàng kinh doanh gồm $17$ chiếc. Trước khi hoàn thiện mỗi chiếc cột là một khối bê tông cốt thép hình lăng trụ lục giác đều có cạnh $14cm$; sau khi hoàn thiện (bằng cách trát thêm vữa tổng hợp vào xung quanh) mỗi cột là một khối trụ có đường kính đáy bằng$30cm$. Biết chiều cao của mỗi cột trước và sau khi hoàn thiện là $390cm$. Tỉnh lượng vữa hỗn hợp cần dùng (tính theo đơn vị ${m^3}$, làm tròn đến $1$ chữ số thập phân sau dấu phầy). Ta có kết quả:

Cho điểm $A(0 ; 8 ; 2)$ và mặt cầu $(S)$ có phương trình $(S):{\left( {x - 5} \right)^2} + {\left( {y + 3} \right)^2} + {\left( {z - 7} \right)^2} = 72$ và điểm $B(1 ; 1 ; -9)$. Viết phương trình mặt phẳng $(P)$ qua $A$ tiếp xúc với $(S)$ sao cho khoảng cách từ $B$ đến $(P)$ là lớn nhất. Giả sử $\overrightarrow n  = \left( {1;m;n} \right)$ là véctơ pháp tuyến của $(P)$. Lúc đó:

Cho hai hàm số $y = \dfrac{{2x - 1}}{{{m^2} - 8 - x}}$  và $y = \dfrac{{5 - 2x}}{{x + 4}}$. Tập hợp các giá trị của tham số $m$ để hai đường tiệm cận đứng của hai đồ thị hàm số trên trùng nhau là:

Cho hai điểm $A\left( {1; - 2;0} \right),B\left( {0;1;1} \right)$, độ dài đường cao $OH$ của tam giác $OAB$ là:

Trong không gian với hệ tọa độ Oxyz cho điểm $A(1;2;1)$và đường thẳng $(d):\dfrac{x}{3} = \dfrac{{y - 1}}{4} = z + 3$. Viết phương trình mặt phẳng (P) đi qua A và chứa đường thẳng d

Tìm hệ số của ${x^6}$ trong khai triển ${\left( {\dfrac{1}{x} + {x^3}} \right)^{3n\, + \,1}}$ với $x \ne 0,$ biết $n$ là số nguyên dương thỏa mãn điều kiện $3C_{n\, + 1}^2 + n{P_2} = 4A_n^2.$

Cho hàm số $f\left( x \right) = \tan \left( {x - \dfrac{{2\pi }}{3}} \right)$. Giá trị $f'\left( 0 \right)$ bằng:

Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông tâm $O$, cạnh $a$. Cạnh bên $SA$ vuông góc với đáy, góc $\widehat {SBD} = {60^0}$. Tính khoảng cách $d$ giữa hai đường thẳng $AB$ và $SO.$

Cho hình chóp $S.ABCD$ có đáy là hình thang vuông $ABCD$ vuông tại $A$ và $D$, $AB = 2a,$ $AD = CD = a$. Cạnh bên $SA = a$ và vuông góc với mặt phẳng $\left( {ABCD} \right).$ Gọi $\varphi$ là góc giữa hai mặt phẳng $\left( {SBC} \right)$ và $\left( {ABCD} \right)$ . Mệnh đề nào sau đây đúng?

Xét số phức $z$ thỏa mãn $\left| {z + 2 - i} \right| + \left| {z - 4 - 7i} \right| = 6\sqrt 2$. Gọi $m,M$ lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của $\left| {z - 1 + i} \right|$. Tính $P = m + M$.

Cho hàm số $f\left( x \right);\,\,g\left( x \right);\,\,h\left( x \right)=\frac{f\left( x \right)}{3-g\left( x \right)}$. Hệ số góc của các tiếp tuyến của các đồ thị hàm số đã cho tại điểm có hoành độ ${{x}_{0}}=2018$ bằng nhau và khác 0. Khẳng định nào sau đây là đúng?

Cho phương trình ${\log _2}\left( {x - \sqrt {{x^2} - 1} } \right).{\log _5}\left( {x - \sqrt {{x^2} - 1} } \right) = {\log _m}\left( {x + \sqrt {{x^2} - 1} } \right)$. Có bao nhiêu giá trị nguyên dương khác 1 của m sao cho phương trình đã cho có nghiệm x lớn hơn 2 ? 

Trong không gian với hệ tọa độ $Oxyz$, cho mặt phẳng $\left( P \right):x + 2y - 3z + 4 = 0$ và đường thẳng $d:\dfrac{{x + 2}}{1} = \dfrac{{y - 2}}{1} = \dfrac{z}{{ - 1}}$. Đường thẳng $\Delta$ nằm trong $\left( P \right)$ đồng thời cắt và vuông góc với $d$ có phương trình:

Cho hàm số $f\left( x \right)={{x}^{3}}-3{{x}^{2}}.$ Có bao nhiêu giá trị nguyên của $m$ để đồ thị hàm số $g\left( x \right)=f\left( \left| x \right| \right)+m$ cắt trục hoành tại 4 điểm phân biệt ?

Trong không gian với hệ tọa độ $Oxyz$, cho mặt cầu $(S) : {\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 3} \right)^2} = 9$ và mặt phẳng  $(P) :2x - 2y + z + 3 = 0$. Gọi $M(a ; b ; c)$ là điểm trên mặt cầu $(S)$ sao cho khoảng cách từ $M$ đến mặt phẳng $(P)$ là lớn nhất. Khi đó:

Phương trình ${\log _3}\dfrac{{{x^2} - 2x + 1}}{x} + {x^2} + 1 = 3x$ có tổng tất cả các nghiệm bằng: