Đề kiểm tra giữa học kì 1- Đề số 2

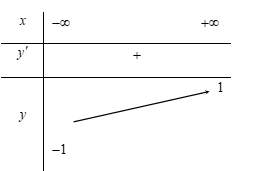
Cho hàm số \(y = f\left( x \right)\) có\(\mathop {\lim }\limits_{x \to  + \infty } f\left( x \right) = 1;\,\mathop {\lim }\limits_{x \to  - \infty } f\left( x \right) =  - 1.\) Khẳng định nào sau đây là khẳng định đúng?

Cho hình chóp tứ giác $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$, \(SA \bot (ABCD)\) và \(SA = a\sqrt 6 \). Thể tích của khối chóp $S.ABCD$ bằng

Tiệm cận ngang của đồ thị hàm số \(y = \dfrac{{x - 1}}{{ - 3x + 2}}\) là?

Chọn khẳng định đúng:

Cho hàm số \(y = f\left( x \right)\) có $\mathop {\lim }\limits_{x \to  + \infty } f\left( x \right) = 0$ và $\mathop {\lim }\limits_{x \to  - \infty } f\left( x \right) =  + \infty $. Mệnh đề nào sau đây là đúng?

Hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = {\left( {x - 1} \right)^2}\left( {x - 3} \right)\) . Phát biểu nào sau đây là đúng ?

Cho hàm số $y = f\left( x \right)$ có đồ thị như hình bên. Giá trị lớn nhất của hàm số này trên đoạn $\left[ { - 2;3} \right]$ bằng:

Hai hình chóp tam giác đều có chung đáy là tam giác đều và đỉnh thuộc hai phía khác nhau so với mặt đáy. Hai hình này bằng nhau khi:

Số mặt phẳng đối xứng của hình bát diện đều là:

Cho hàm số \(y=\dfrac{2x+1}{x-2}\). Khẳng định nào dưới đây là đúng?

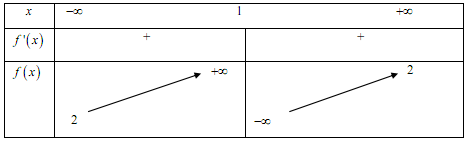
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình bên. Số đường tiệm cận ngang của đồ thị hàm số \(y = f\left( x \right)\) là:

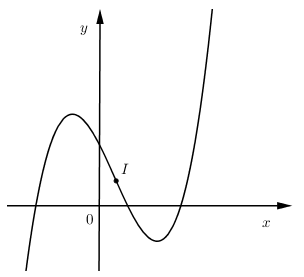
Hàm số $y = f\left( x \right) = a{x^3} + b{x^2} + cx + d$ có đồ thị như hình vẽ, chọn kết luận đúng:

Tìm tất cả các giá trị của $m$ để hàm số $y = \dfrac{{m{x^3}}}{3} - m{x^2} + x - 1$  có cực đại và cực tiểu.

Trong các khẳng định sau, khẳng định nào sai?

Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên như sau:

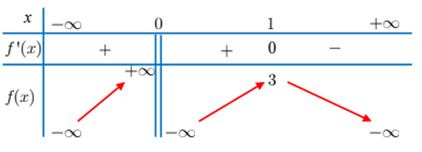
Với các giá trị thực của tham số \(m\), phương trình \(f\left( x \right)=m\) có nhiều nhất bao nhiêu nghiệm?

Giá trị lớn nhất của hàm số $y = x - \dfrac{1}{x}$ trên $\left( { - \infty ; - 1} \right]$ là:

Cho hàm số \(y = f\left( x \right)\) đồng biến trên \(\left( { - 3;7} \right)\) và xác định tại hai điểm \(x =  - 3;x = 7\). Chọn kết luận đúng:

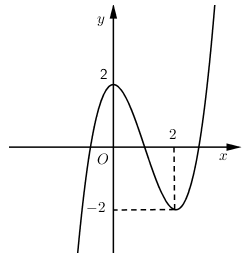
Đường cong trong hình vẽ bên là đồ thị của hàm số nào?

Cho điểm $A \in \left( P \right),B \notin \left( P \right)$, gọi \(B'\) là ảnh của \(B\) qua phép đối xứng qua mặt phẳng \(\left( P \right),A \notin BB'\). Chọn kết luận đúng:

Vật thể nào trong các vật thể sau không phải là khối đa diện?

Số cực trị của hàm số \(y = \dfrac{{ax + b}}{{cx + d}}\) là:

Cho hai đồ thị hàm số $y = {x^3} + 2{x^2} - x + 1$ và đồ thị hàm số $y = {x^2} - x + 3$ có tất cả bao nhiêu điểm chung?

Khối đa diện lồi có \(8\) đỉnh và \(6\) mặt thì có số cạnh là:

Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông. Nếu khối chóp có chiều cao bằng \(a\sqrt 3 \) và thể tích là \(3{a^3}\sqrt 3 \) thì cạnh đáy có độ dài là:

Khối đa diện đều loại \(\left\{ {n;p} \right\}\) thì \(n\) là:

Cho lăng trụ đều \(ABC.A'B'C'\), cạnh đáy bằng a, góc giữa hai mặt phẳng \(\left( {A'BC} \right)\) và \(\left( {ABC} \right)\) bằng \(60^\circ \). Tính thể tích khối lăng trụ đó.

Trong các hàm số dưới đây, hàm số nào không đồng biến trên $R?$

Cho khối chóp tam giác \(S.ABC\), trên các cạnh \(SA,SB,SC\) lần lượt lấy các điểm \(A',B',C'\). Khi đó:

Cho khối chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh \(a\), \(SA \bot \left( {ABC} \right)\) và \(SA = a\). Tính thể tích khối chóp \(S.ABC\).

Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như sau. Khẳng định nào dưới đây là đúng?

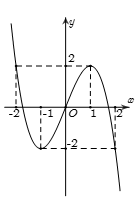
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ. Mệnh đề nào sau đây SAI?

Cho hình chóp đều \(S.ABCD\) có cạnh \(AB = a\), góc giữa đường thẳng \(SA\) và mặt phẳng \(\left( {ABC} \right)\) bằng \(45^0\). Thể tích khối chóp \(S.\,ABCD\) là

Hàm số $y = {x^3} - 6{x^2} + mx + 1$ đồng biến trên $\left( {0; + \infty {\rm{\;}}} \right)$ khi giá trị của $m$ là:

Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:

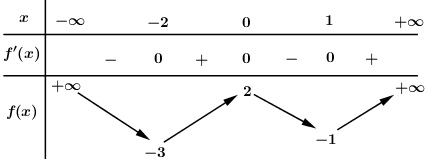
Số điểm cực tiểu của hàm số \(g\left( x \right) = {f^3}\left( x \right) - 3f\left( x \right)\) là:

Cho hàm số \(y = {x^3} - 3{x^2} - 9x + m\). Viết phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số.

Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 1;4} \right]\) và có đồ thị như hình vẽ

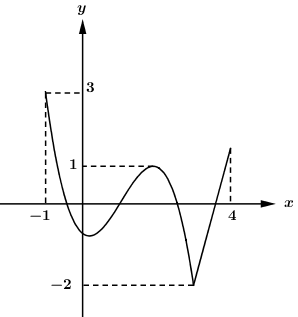
Có tất cả bao nhiêu giá trị nguyên của m thuộc đoạn \(\left[ { - 10;10} \right]\) để bất phương trình \(\left| {f\left( x \right) + m} \right| < 2m\) đúng với mọi x thuộc đoạn \(\left[ { - 1;4} \right]\)?

Cho điểm $I\left( {0;4} \right)$ và đường cong $\left( C \right):y =  - {x^2} + 3x$. Phương trình $\left( C \right)$ đối với hệ tọa độ $\left( {IXY} \right)$ là:

Phương trình đường tiệm cận đứng của đồ thị hàm số $y = \dfrac{{{x^2} - 3x - 4}}{{{x^2} - 16}}$ là:

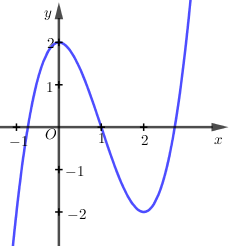
Đồ thị trong hình dưới là đồ thị của một trong bốn hàm số cho trong các phương án sau đây, đó là hàm số nào?

Đồ thị hàm số \(y = \dfrac{{2x + b}}{{cx + d}}\) như hình vẽ bên:

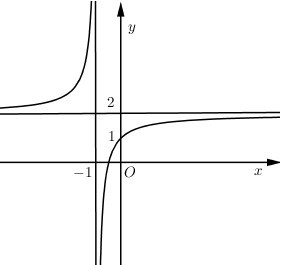
Chọn kết luận đúng:

Đồ thị hàm số $y = \dfrac{{2x + b}}{{cx + d}}$ như hình vẽ bên

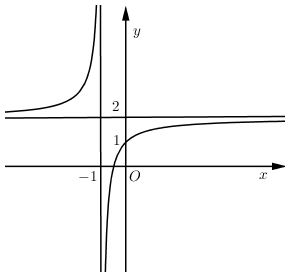
Chọn khẳng định đúng:

Cho hàm số \(y=\frac{x-1}{2x-3}\). Gọi I là giao điểm của hai tiệm cận của đồ thị hàm số. Khoảng cách từ I  đến tiếp tuyến của đồ thị hàm số đã cho đạt giá trị lớn nhất bằng

Cho hàm số \(y = f\left( x \right) = a{x^3} + b{x^2} + cx + d\). Biết \(f\left( {x + 1} \right) = {x^3} + 3{x^2} + 3x + 2\). Hãy xác định biểu thức \(f\left( x \right)\).

Cho khối lăng trụ tam giác đều \(ABC.{A_1}{B_1}{C_1}\) có tất cả các cạnh bằng \(a\). Gọi \(M\) là trung điểm của \(A{A_1}\). Thể tích khối chóp \(M.BC{A_1}\) là:

Cho khối lăng trụ đứng \(ABC.A'B'C'\) có đáy ABC là tam giác vuông tại B với \(AB = a,AA' = 2a,\)\(A'C = 3a\)  . Gọi M là trung điểm của \(A'C'\), I là giao điểm của đường thẳng AM và A’C. Tính theo a thể tích khối IABC .

Cho tứ diện \(ABCD\) có \(AD = 14,BC = 6\). Gọi \(M,N\) lần lượt là trung điểm của các cạnh \(AC,BD\) và \(MN = 8\). Gọi \(\alpha \) là góc giữa hai đường thẳng \(BC\) và \(MN\). Tính \(\sin \alpha \).

Cho hình hộp đứng $ABCD.A’B’C’D’$ có đáy $ABCD$ là hình thoi cạnh $a$ và $\widehat {BAD} = {60^0}$, $AB’$ hợp với đáy $(ABCD)$ một góc ${30^0}$. Thể tích của khối hộp là

Cho hàm số \(y = f\left( x \right)\). Đồ thị hàm \(y = f'\left( x \right)\) như hình vẽ

Đặt \(g\left( x \right) = 3f\left( x \right) - {x^3} + 3x - m\), với \(m\) là tham số thực. Điều kiện cần và đủ để bất phương trình \(g\left( x \right) \ge 0\) đúng với \(\forall x \in \left[ { - \sqrt 3 ;\sqrt 3 } \right]\) là:

Cho các số thực $x, y$ thỏa mãn ${\left( {x - 4} \right)^2} + {\left( {y - 4} \right)^2} + 2xy \leqslant 32.$ Giá trị nhỏ nhất $m$ của biểu thức $A = {x^3} + {y^3} + 3\left( {xy - 1} \right)\left( {x + y - 2} \right)$ là:

Cho hàm số \(y = f\left( x \right) = a{x^4} + b{x^2} + c\) biết \(a > 0\), \(c > 2017\) và \(a + b + c < 2017\). Số điểm cực trị của hàm số \(y = \left| {f\left( x \right) - 2017} \right|\) là: