Cho hàm số \(y=\frac{x-1}{2x-3}\). Gọi I là giao điểm của hai tiệm cận của đồ thị hàm số. Khoảng cách từ I  đến tiếp tuyến của đồ thị hàm số đã cho đạt giá trị lớn nhất bằng

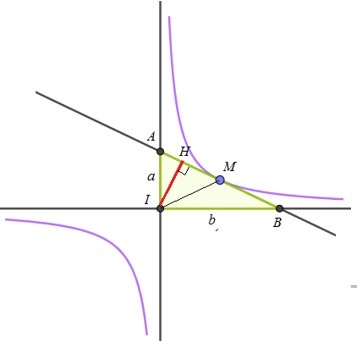
Gọi độ dài đoạn thẳng IA, IB lần lượt là a, b.

Kẻ \(IH\bot AB,\,H\in AB\).

Tam giác IAB vuông tại I, \(IH\bot AB\)

\(\begin{array}{l} \Rightarrow \frac{1}{{I{H^2}}} = \frac{1}{{I{A^2}}} + \frac{1}{{I{B^2}}} \Leftrightarrow I{H^2} = \frac{{I{A^2}.I{B^2}}}{{I{A^2} + I{B^2}}}\\\mathop  \le \limits^{{\mathop{\rm Cos}\nolimits} i} \frac{{I{A^2}.I{B^2}}}{{2IA.IB}} = \frac{{IA.IB}}{2} = {S_{IAB}} = const\end{array}\)

\(\Rightarrow I{{H}_{\max }}=\sqrt{{{S}_{IAB}}}\) khi và chỉ khi \(IA=IB\).

Khi đó, tam giác IAB vuông cân tại I, M trùng H.

\(\Rightarrow \)Ta tìm M bằng cách tìm giao điểm của đường thẳng IM với đồ thị (C).

 *) Viết phương trình đường thẳng IM:

Ta có: \(y=\frac{x-1}{2x-3}\Rightarrow y'=\frac{-1}{{{(2x-3)}^{2}}}<0,\,\,\forall x\ne \frac{3}{2}\): Hàm số nghịch biến trên các khoảng \(\left( -\infty ;\frac{3}{2} \right),\,\,\left( \frac{3}{2};+\infty  \right)\).

( Đồ thị hàm số có dạng như hình vẽ bên).

Đường thẳng IM là đường thẳng đi qua điểm \(I\left( \frac{3}{2};\frac{1}{2} \right)\) song song với phân giác của góc phần tư thứ nhất : \(y=x\), có phương trình là: \(y=x-1\).

Tọa độ điểm M là nghiệm của hệ phương trình :

       \(\left\{ \begin{array}{l}y = x - 1\\y = \frac{{x - 1}}{{2x - 3}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = x - 1\\x - 1 = \frac{{x - 1}}{{2x - 3}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = x - 1\\(x - 1)(2x - 3 - 1) = 0,\,\,x \ne \frac{3}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = x - 1\\\left[ \begin{array}{l}x = 1\\x = 2\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x = 1\\y = 0\end{array} \right.\\\left\{ \begin{array}{l}x = 2\\y = 1\end{array} \right.\end{array} \right.\)

 Vậy \(M\left( 1;0 \right)\) hoặc \(M\left( 2;1 \right)\).

*) Khoảng cách từ I đến đường tiếp tuyến của (C) tại M :

    \(IH=IM=\sqrt{{{\left( 1-\frac{3}{2} \right)}^{2}}+{{\left( 0-\frac{1}{2} \right)}^{2}}}=\sqrt{{{\left( 2-\frac{3}{2} \right)}^{2}}+{{\left( 1-\frac{1}{2} \right)}^{2}}}=\frac{\sqrt{2}}{2}\)