Cho hàm số \(y = f\left( x \right)\) có $\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 0$ và $\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = + \infty $. Mệnh đề nào sau đây là đúng?
Trả lời bởi giáo viên
Vì $\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 0$ và $\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = + \infty $ nên đồ thị hàm số chỉ một tiệm cận ngang là trục hoành.
Hướng dẫn giải:
Sử dụng định nghĩa tiệm cận ngang:
Đường thẳng \(y = {y_0}\) được gọi là TCN của đồ thị hàm số nếu \(\mathop {\lim }\limits_{x \to + \infty } y = {y_0}\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } y = {y_0}\)
Giải thích thêm:
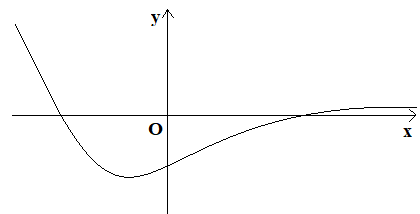
Đáp án D sai vì chưa chắc đồ thị hàm số nằm hoàn toàn phía trên trục hoành, có thể xảy ra trường hợp dưới đây: