Đề thi thử THPTQG môn Toán sở GD&ĐT tỉnh Hà Tĩnh năm 2021-2022

Cho số phức \(z =  - 2 + 3i\). Số phức liên hợp của \(z\) là

Phương trình mặt cầu có tâm  \(I\left( { - 1;2; - 3} \right)\), bán kính R=3 là

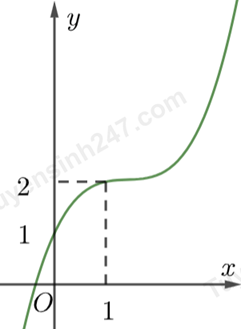
Điểm nào dưới đây thuộc đồ thị hàm số \(y = {x^3} - 3x + 3\)?

Một mặt cầu có bán kính \(R\sqrt 3 \) thì có diện tích bằng

Nguyên hàm của hàm số \(f\left( x \right) = {x^{2022}}\)\((x \in \mathbb{R})\) là hàm số nào trong các hàm số dưới đây?

Cho hàm số \(y = f(x)\) như hình vẽ. Đồ thị hàm số \(y = f(x)\) có mấy điểm cực trị?

Tập nghiệm của bất phương trình \({\left( {\dfrac{1}{3}} \right)^{2x - 1}} \ge \dfrac{1}{3}\) là

Cho hình chóp có diện tích đáy là \(2{a^2}\). chiều cao là $3a$. Khi đó thể tích khối chóp này là

Hàm số \(y = {\left( {1 - 2x} \right)^{\sqrt 2 }}\) có tập xác định là:

Phương trình \(\log \left( {3x + 1} \right) = 1\) có nghiệm là:

Cho hàm số \(f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\), \(f\left( { - 1} \right) =  - 2\) và \(f\left( 3 \right) = 2\). Tính \(I = \int\limits_{ - 1}^3 {f'\left( x \right)} dx.\)

Phần thực và phần ảo số phức \(z = (1 + 2i)i\) là

Trong không gian với hệ toạ độ $Oxyz$. Điểm nào sau đây không thuộc mặt phẳng (P):\( - 2x + y - 5 = 0\)

Trong không gian với hệ tọa độ Oxyz, cho vectơ \(\overrightarrow a \left( {1; - 2; - 3} \right)\)  và \(\overrightarrow b  =  - 2\overrightarrow a \). Tìm tọa độ của vectơ \(\overrightarrow b \)?

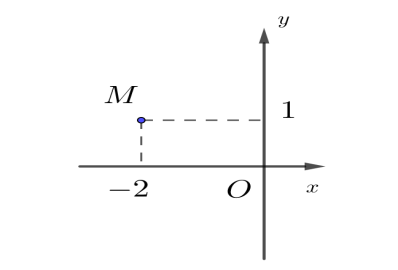
Cho số phức \(z\) có điểm biểu diễn trên mặt phẳng tọa độ là điểm \(M\) như hình vẽ. Tính mô dun của \(z\).

Tiệm cận ngang của đồ thị hàm số \(y = \dfrac{{1 - 2x}}{{ - x + 2}}\) là

Tính giá trị của biểu thức \(P = {2^{{{\log }_2}3}} - {\log _{\sqrt 3 }}3\).

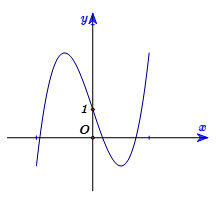
Đường cong sau đây là đồ thị của hàm số nào?

Trong các điểm sau điểm nào không thuộc đường thẳng \(d:\dfrac{{x - 1}}{2} = \dfrac{{y + 1}}{{ - 1}} = \dfrac{{z + 3}}{3}\).

 Cho \(n,k\) là các số tự nhiên \(1 \le k \le n\). Trong các công thức sau công thức nào đúng?

Cho hình chóp có diện tích đáy bằng \(5\), đường cao bằng 3. Thể tích khối chóp là

Đạo hàm của hàm số \(y = {5^x}\) là

Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:

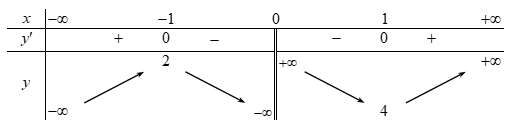
Hàm số nghịch biến trong khoảng nào?

Cho hình nón \(\left( N \right)\) có chiều cao \(h\), độ dài đường sinh \(l\), bán kính đáy \(r\). Ký hiệu \({S_{xq}}\) là diện tích xung quanh của \(\left( N \right)\). Công thức nào sau đây là đúng?

Cho hàm số \(f\) liên tục trên \(\mathbb{R}\) và số thực dương \(a\). Trong các khẳng định sau, khẳng định nào luôn đúng?

Cho cấp số nhân biết \({u_1} =  - 2\), công bội \(q = 3\). Tính \({u_4}\).

Tính \(I = \int {{3^x}} {\rm{dx}}\).

Cho hàm số \(y = f\left( x \right)\) xác định và liên tục trên \(\mathbb{R}\), có đồ thị như hình vẽ.

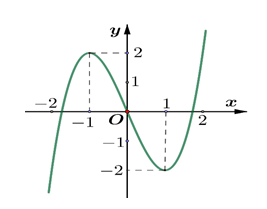
Hàm số \(y = f\left( x \right)\) có điểm cực tiểu là

Giá trị lớn nhất của hàm số \(f\left( x \right) = {x^3} - 3x + 2\) trên đoạn \(\left[ { - 3\,;\,3} \right]\) bằng:

Hàm số \(y =  - {x^4} + 2{x^2} + 1\) đồng biến trên khoảng nào dưới đây?

Cho \({\log _a}b = 3\) với \(a\), \(b\) là các số thực dương và \(1\) khác \(1\). Giá trị biểu thức \(T = {\log _{{a^2}}}{b^8} + {\log _{\sqrt a }}b\) bằng

Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) (tham khảo hình vẽ). Góc giữa hai đường thẳng \(A'C'\) và \(BB'\) bằng

Cho \(\int\limits_2^4 {f\left( x \right){\rm{d}}x}  = 8\). Kết quả \(\int\limits_2^4 {\left[ {2 - 3{x^2} - f\left( x \right)} \right]{\rm{d}}x} \) bằng

Trong không gian \(Oxyz\), đường thẳng \(\Delta \) đi qua\(A\left( {1;\,2;\, - 3} \right)\) và vuông góc với mặt phẳng \(x - 2y + 4z - 3 = 0\) có phương trình là

Cho số phức \(z\) thỏa mãn \(z\left( {1 - i} \right) + 2 = 4 + i\). Phần ảo của \(\bar z\) là

Cho hình chóp \(S.ABCD\) có \(SA \bot \left( {ABCD} \right)\), đáy \(ABCD\) là hình vuông cạnh \(a\), \(SA = a\sqrt 3 \). Khoảng cách từ \(A\) đến \(\left( {SCD} \right)\) bằng?

Một tổ có 10 đoàn viên trong đó có 4 đoàn viên nam và 6 đoàn viên nữ. Chọn 3 đoàn viên đi chăm sóc cây cảnh. Tính xác suất để trong 3 đoàn viên được chọn có ít nhất 1 đoàn viên nữ.

Trong không gian \(Oxyz\), cho điểm \(A( - 1;5;4)\) và đường thẳng \(d:\,\dfrac{{x - 2}}{1} = \dfrac{{y + 3}}{2} = \dfrac{z}{{ - 5}}\). Đường thẳng đi qua \(A\) và song song với đường thẳng \(d\) có phương trình tham số là

Có bao nhiêu số nguyên $x$ thỏa mãn \(\left( {{{25}^x} - {{126.5}^{x + 1}} + 3125} \right)\sqrt {3 - {{\log }_2}x}  \le 0\)?

Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình bên.

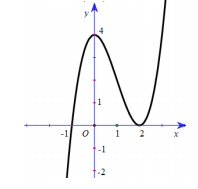
Số nghiệm dương của phương trình \(f'\left( {f\left( x \right) - 2} \right) = 0\) là

Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và \(\int\limits_0^2 {f\left( x \right){\rm{d}}x}  = 9;\,\int\limits_0^4 {f\left( x \right){\rm{d}}x}  = 12\). Giá trị của \(\int\limits_{ - 1}^1 {f\left( {\left| {3x - 1} \right|} \right){\rm{d}}x} \) bằng

Cho hình chóp \(S.ABCD\) với đáy \(ABCD\) là hình thang vuông tại \(A\) và \(D\), đáy nhỏ của hình thang là \(CD\), cạnh bên \(SC = 2a\). Tam giác \(SAD\) là tam giác đều cạnh \(a\) và nằm trong mặt phẳng vuông góc với đáy hình chóp. Gọi \(H\) là trung điểm cạnh \(AD\), khoảng cách từ \(B\) tới mặt phẳng \(\left( {SHC} \right)\) bằng \(a\sqrt 3 \). Tính thể tích \(V\) của khối chóp \(S.ABCD\)?

Trên tập hợp các số phức, xét phương trình \({z^2} + 4az + {b^2} + 1 = 0\), (\(a,\,\,b\) là các tham số thực). Có bao nhiêu cặp số thực \(\left( {a;\,b\,} \right)\)sao cho phương trình đó có hai nghiệm \({z_1},\,{z_2}\) thỏa mãn \({z_1} + 2i{z_2} = 3 + 4i\)?

Xét hai số phức \({z_1}\,,\,{z_2}\) thỏa mãn \(2\left| {{{\bar z}_1} + i} \right| = \left| {{{\bar z}_1} - {z_1} - 2i} \right|\) và \(\left| {{z_2} - i - 10} \right| = 1\). Giá trị nhỏ nhất của biểu thức \(\left| {{z_1} - {z_2}} \right|\) bằng

Cho hàm số bậc ba \(y = f\left( x \right)\) có đồ thị là đường cong trong hình bên dưới:

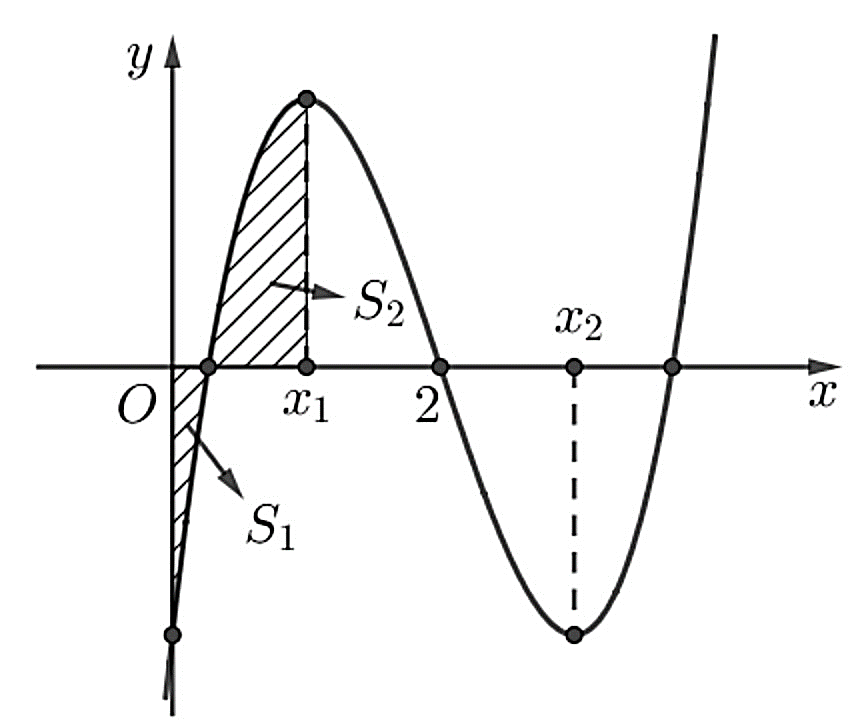
Biết hàm số \(f\left( x \right)\) đạt cực trị tại các điểm \({x_1},\,\,{x_2}\) sao cho \({x_2} - {x_1} = 2\) và \(f''\left( 2 \right) = 0\). Gọi \({S_1}\) và \({S_2}\) là diện tích hai hình phẳng được gạch trong hình bên. Tỉ số \(\dfrac{{{S_1}}}{{{S_2}}}\) bằng

Trong không gian với hệ tọa độ \(Oxyz\), cho điểm \(M\left( {1;1;1} \right)\) và hai đường thẳng \({d_1}:\dfrac{{x - 2}}{1} = \dfrac{{y + 3}}{{ - 1}} = \dfrac{{z - 1}}{2}\), \({d_2}:\left\{ \begin{array}{l}x =  - 1 + t\\y = 2 + 2t\\z = 1 + t\end{array} \right.\). Đường thẳng \(\Delta \) đi qua điểm \(M\) vuông góc với \({d_1}\) và cắt \({d_2}\) có phương trình là

Một người thợ có một khối đá hình trụ. Kẻ hai đường kính \(MN,\,PQ\) của hai đáy sao cho \(MN \bot PQ.\) Người thợ đó cắt khối đá theo các mặt cắt đi qua 3 trong 4 điểm \(M,\,N,\,P,\,Q\) để thu được khối đá có hình tứ diện \(MNPQ\). Biết rằng \(MN = 6\,{\rm{dm}}\) và thể tích khối tứ diện \(MNPQ\) bằng \(36{\rm{d}}{{\rm{m}}^3}\). Tìm thể tích của lượng đá bị cắt bỏ (làm tròn kết quả đến 1 chữ số thập phân).

Có bao nhiêu cặp số nguyên \(\left( {x;y} \right)\) thỏa mãn \(0 \le x \le 2022\), \(y \ge 2\) và \({x^2} + x - xy = x{\log _2}\left( {xy - x} \right) - {2^x}\)?

Cho hai mặt cầu \(\left( S \right):{\left( {x - 1} \right)^2} + {y^2} + {\left( {z - 3} \right)^2} = 36\) và \(\left( {S'} \right):{\left( {x + 1} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z - 1} \right)^2} = 81\). Gọi \(d\) là đường thẳng tiếp xúc với cả hai mặt cầu trên và cách điểm \(M\left( {4; - 1; - 7} \right)\) một khoảng lớn nhất. Gọi \(E\left( {m;n;p} \right)\) là giao điểm của \(d\) với mặt phẳng \(\left( P \right):2x - y + z - 17 = 0\). Biểu thức \(T = m + n + p\) có giá trị bằng

Cho hàm số \(y = f(x)\) có đạo hàm \(f'(x) = {\left( {x - 1} \right)^2}\left( {{x^2} - 2x} \right)\) với mọi \(x \in \mathbb{R}\). Có bao nhiêu giá trị nguyên dương của tham số \(m\) để hàm số \(g(x) = f\left( {{x^2} - 8x + m} \right)\) có đúng \(5\) điểm cực trị?