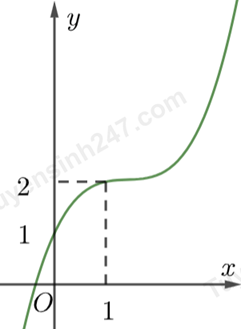
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình bên.

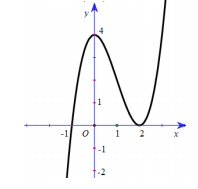
Số nghiệm dương của phương trình \(f'\left( {f\left( x \right) - 2} \right) = 0\) là

Đặt \(t =  f\left( x \right)-2\)

Từ đồ thị hàm số \(y = f\left( x \right)\), ta có hàm số có 2 điểm cực trị là $x=0$ và $x=2$. Khi đó phương trình $f’(t)=0$ có 2 nghiệm phân biệt $t=0$ và $t=2$. Do đó:

\(f'\left( {f\left( x \right) -2} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) - 2 = 0\\f\left( x \right) - 2 = 2\end{array} \right.\) \( \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) = 2\\f\left( x \right) = 4\end{array} \right.\).

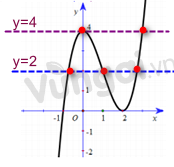
Dựa vào đồ thị ta có:

Phương trình \(f\left( x \right) = 2\) có hai nghiệm dương (2 điểm bên phải trục tung).

Phương trình \(f\left( x \right) = 4\) có một nghiệm dương (1 điểm bên phải trục tung) khác hai nghiệm của phương trình \(f\left( x \right) = 2\).

Vậy phương trình \(f'\left( {f\left( x \right) - 2} \right) = 0\) có ba nghiệm dương.