Cho hình chóp \(S.ABCD\) với đáy \(ABCD\) là hình thang vuông tại \(A\) và \(D\), đáy nhỏ của hình thang là \(CD\), cạnh bên \(SC = 2a\). Tam giác \(SAD\) là tam giác đều cạnh \(a\) và nằm trong mặt phẳng vuông góc với đáy hình chóp. Gọi \(H\) là trung điểm cạnh \(AD\), khoảng cách từ \(B\) tới mặt phẳng \(\left( {SHC} \right)\) bằng \(a\sqrt 3 \). Tính thể tích \(V\) của khối chóp \(S.ABCD\)?

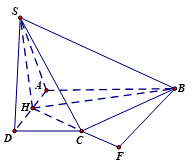
\(\left\{ \begin{array}{l}\left( {SAD} \right) \bot \left( {ABCD} \right)\\\left( {SAD} \right) \cap \left( {ABCD} \right) = AD\\SH \bot AD,SH \subset \left( {SAD} \right)\end{array} \right. \)\(\Rightarrow SH \bot \left( {ABCD} \right)\)  \(\Rightarrow(SHC) \bot \left( {ABCD} \right)\)

Ta có \(SH = \sqrt {S{D^2} - D{H^2}}  = \dfrac{{a\sqrt 3 }}{2}\), \(HC = \sqrt {S{C^2} - S{H^2}}  = \sqrt {4{a^2} - \dfrac{{3{a^2}}}{4}}\)\(  = \dfrac{{\sqrt {13} a}}{2}\).

\(CD = \sqrt {H{C^2} - H{D^2}}  = \sqrt {\dfrac{{13{a^2}}}{4} - \dfrac{{{a^2}}}{4}}\)\(    = a\sqrt 3 \).

Trong $(ABCD)$, vẽ \(BF \bot HC\)

Ta có \(\left\{ \begin{array}{l}BF \bot HC\\BF \bot SH\end{array} \right. \Rightarrow BF \bot \left( {SHC} \right)\) nên \(d\left( {B,\left( {SHC} \right)} \right) = BF = a\sqrt 3 \).

\({S_{HBC}} = \dfrac{1}{2}BF.HC = \dfrac{1}{2}.\sqrt 3 a.\dfrac{{\sqrt {13} a}}{2} \)\(  = \dfrac{{\sqrt {39} {a^2}}}{4}\)

Đặt \(AB = x\) nên \({S_{AHB}} = \dfrac{1}{2}AH.AB = \dfrac{a}{4}.x\); \({S_{CDH}} = \dfrac{1}{2}DH.DC = \dfrac{{{a^2}\sqrt 3 }}{4}\)

\({S_{ABCD}} = \dfrac{1}{2}\left( {CD + AB} \right)AD \) \( = \dfrac{{\left( {a\sqrt 3  + x} \right)a}}{2}\).

\({S_{AHB}} = {S_{ABCD}} - {S_{CDH}} - {S_{BHC}}\)\( \Leftrightarrow \dfrac{a}{4}.x = \dfrac{{\left( {a\sqrt 3  + x} \right)a}}{2} - \dfrac{{{a^2}\sqrt 3 }}{4} \) \( - \dfrac{{{a^2}\sqrt {39} }}{4}\) \( \Leftrightarrow x = \left( {\sqrt {39}  - \sqrt 3 } \right)a\).

\({S_{ABCD}} = \left[ {a\sqrt 3  + \left( {\sqrt {39}  - \sqrt 3 } \right)a} \right]\dfrac{a}{2}\)\(   = \dfrac{{\sqrt {39} {a^2}}}{2}\)

Vậy \({V_{S.ABCD}} = \dfrac{1}{3}SH.{S_{ABCD}} \) \( = \dfrac{1}{3}.\dfrac{{a\sqrt 3 }}{2}.\dfrac{{\sqrt {39} {a^2}}}{2}\) \( = \dfrac{{\sqrt {13} {a^3}}}{4}\).