Đề kiểm tra học kì 2 - Đề số 3

Nếu \(\overrightarrow a ,\overrightarrow b \) là cặp VTCP của \(\left( P \right)\) thì véc tơ nào sau đây có thể là VTPT của \(\left( P \right)\)?

Trong không gian với hệ trục tọa độ Oxyz, cho 2 điểm \(A(2;1;0),\,\,B(1;-1;3)\). Mặt phẳng qua AB và vuông góc với mặt phẳng (P): \(x+3y-2z-1=0\) có phương trình là

Tích phân \(\int\limits_{1}^{3}{{{e}^{x}}dx}\) bằng:

Gọi \({z_1};{z_2}\) là hai nghiệm phức của phương trình \({z^2} + 2z + 5 = 0\). Tính \(\left| {{z_1}} \right| + \left| {{z_2}} \right|\).

Chọn mệnh đề đúng:

Trong không gian với hệ tọa độ $Oxyz$, mặt cầu $\left( S \right)$ có tâm $I\left( {1,2, - 3} \right)$ và đi qua điểm $A\left( {1,0,4} \right)$ có phương trình là

Tìm nguyên hàm của hàm số \(f\left( x \right)=3\cos x+\dfrac{1}{{{x}^{2}}}\) trên \(\left( 0;\,+\infty \right)\).

Cho hàm số \(f\left( x \right)\) liên tục trên đoạn \(\left[ {a;b} \right]\). Chọn mệnh đề sai?

Kí hiệu \(a,b\) lần lượt là phần thực và phần ảo của số phức \(3 - 2\sqrt 2 i\). Tìm \(a,b.\)

$F\left( x \right)$ là một nguyên hàm của hàm số $f\left( x \right) = \ln x$ và $F\left( 1 \right) = 3.$ Khi đó giá trị của $F\left( e \right)$ là:

Cho \(\overrightarrow a ,\overrightarrow b \) là các VTCP của mặt phẳng \(\left( P \right)\)

. Chọn kết luận sai?

Cho hai số phức ${z_1} = 2017 - i$ và ${z_2} = 2 - 2016i$. Tìm số phức $z = {z_1}.{z_2}.$

Trong không gian với hệ tọa độ Oxyz, cho hai điểm \(A\left( -1;2;-4 \right)\) và \(B\left( 1;0;2 \right)\). Viết phương trình đường thẳng d đi qua hai điểm A và B.

Trong không gian $Oxyz$ cho $3$ véc tơ: \(\vec a\left( {4;2;5} \right),\vec b\left( {3;1;3} \right),\vec c\left( {2;0;1} \right)\). Kết luận nào sau đây đúng 

Cho số phức \(z\) thỏa mãn\(|z - 1 - 2i| = 4\). Gọi $M,m$ lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của \(|z + 2 + i|\). Tính \(S = {M^2} + {m^2}\).

Trong không gian với hệ tọa độ $Oxyz$, xét mặt cầu $\left( S \right)$ đi qua hai điểm $A\left( {1;2;1} \right);B\left( {3;2;3} \right)$, có tâm thuộc mặt phẳng $\left( P \right):x - y - 3 = 0$ , đồng thời có bán kính nhỏ nhất, hãy tính bán kính $R$ của mặt cầu $\left( S \right)$?

Cho hai véc tơ \(\overrightarrow u  = \left( {a;0;1} \right),\overrightarrow v  = \left( { - 2;0;c} \right)\). Biết \(\overrightarrow u  = \overrightarrow v \), khi đó:

Diện tích hình phẳng giới hạn bởi các đồ thị hàm số $y = {x^3} - x;y = 2x$ và các đường thẳng $x =  - 1;x = 1$ được xác định bởi công thức:

Nếu đặt $\left\{ \begin{array}{l}u = \ln \left( {x + 2} \right)\\{\rm{d}}v = x\,{\rm{d}}x\end{array} \right.$ thì tích phân $I = \int\limits_0^1 {x.\ln \left( {x + 2} \right){\rm{d}}x} $ trở thành

Trong không gian với hệ tọa độ \(Oxyz\), cho các điểm \(A\left( {0;0;2} \right)\), \(B\left( {1;0;0} \right)\), \(C\left( {2;2;0} \right)\) và \(D\left( {0;m;0} \right)\). Điều kiện cần và đủ của \(m\) để khoảng cách giữa hai đường thẳng \(AB\) và \(CD\) bằng \(2\) là:

Đặt \(F\left( x \right) = \int\limits_1^x {tdt} \). Khi đó \(F'\left( x \right)\) là hàm số nào dưới đây?

Trong không gian với hệ tọa độ Oxyz, cho hai điểm \(A\left( { - 2; - 1;3} \right)\) và \(B(0;3;1)\). Tọa độ trung điểm của đoạn thẳng AB là

Nếu \(x = u\left( t \right)\) thì:

Tính thể tích khối tròn xoay do hình phẳng giới hạn bởi đường \(\left( E \right):\dfrac{{{x^2}}}{{16}} + \dfrac{{{y^2}}}{9} = 1\) quay quanh \(Oy\,\,?\)

Trong không gian với hệ trục tọa độ $Oxyz$, cho các phương trình sau, phương trình nào không phải là phương trình của mặt cầu?

Tính \(I = \int {x{{\tan }^2}xdx} \) ta được:

Kết quả của tích phân \(\int\limits_{ - 1}^0 {\left( {x + 1 + \dfrac{2}{{x - 1}}} \right)dx} \) được viết dưới dạng \(a + b\ln 2\) với \(a,b \in Q\). Khi đó \(a + b\) có giá trị là:

Tích phân $\int\limits_{ - 1}^5 {\left| {{x^2} - 2x - 3} \right|} dx$ có giá trị bằng:

Cho \(\int\limits_0^b {\frac{{{e^x}}}{{\sqrt {{e^x} + 3} }}dx}  = 2\) với \(b \in K\). Khi đó $K$ có thể là khoảng nào trong các khoảng sau?

Biết \(\int\limits_{0}^{4}{x\ln ({{x}^{2}}+9)dx=a\ln 5+b\ln 3+c}\) trong đó a, b, c là các số nguyên. Giá trị biểu thức \(T=a+b+c\) là

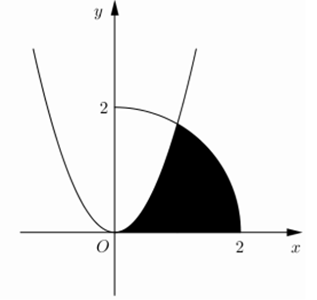
Cho \(\left( H \right)\) là hình phẳng giới hạn bởi parabol  \(y=\sqrt{3}{{x}^{2}}\), cung tròn có phương trình \(y=\sqrt{4-{{x}^{2}}}\) (với \(0\le x\le 2\)) và trục hoành (phần tô đậm trong hình vẽ). Diện tích của \(\left( H \right)\) bằng

Cho (H) là hình phẳng giới hạn bởi đồ thị hàm số \(y=\sqrt{x},\) trục hoành và đường thẳng \(x=9.\) Khi (H) quay quanh trục Ox tạo thành một khối tròn xoay có thể tích bằng:

Thu gọn số phức $w = {i^5} + {i^6} + {i^7} + ... + {i^{18}}$ có dạng \(a + bi\). Tính tổng \(S = a + b.\)

Cho số phức \({\rm{w}}\)và hai số thực \(a,b\). Biết \({z_1} = {\rm{w}} + 2i\) và \({z_2} = 2w - 3\) là 2 nghiệm phức của phương trình \({z^2} + az + b = 0\). Tính \(T = \left| {{z_1}} \right| + \left| {{z_2}} \right|\).

Hỏi có bao nhiêu số phức thỏa mãn đồng thời các điều kiện $\left| {z - i} \right| = 5$ và \({z^2}\) là số thuần ảo?

Cho số phức $z$ thay đổi, luôn có $\left| z \right| = 2$ . Khi đó tập hợp điểm biểu diễn số phức ${\rm{w}} = (1 - 2i)\overline z  + 3i$ là

Biết số phức $z = x + yi{\rm{ }}\left( {x;y \in \mathbb{R}} \right)$ thỏa mãn đồng thời các điều kiện $\left| {z - \left( {3 + 4i} \right)} \right| = \sqrt 5 $ và biểu thức $P = {\left| {z + 2} \right|^2} - {\left| {z - i} \right|^2}$ đạt giá trị lớn nhất. Tính $\left| z \right|$.

Trong không gian với hệ tọa độ \(Oxyz\), cho sáu điểm \(A\left( {1;2;3} \right)\), \(B\left( {2; - 1;1} \right)\), \(C\left( {3;3; - 3} \right)\), \(A',\,\,B',\,\,C'\) thỏa mãn \(\overrightarrow {A'A}  + \overrightarrow {B'B}  + \overrightarrow {C'C}  = \overrightarrow 0 \). Nếu \(G'\) là trọng tâm tam giác \(A'B'C'\) thì \(G'\) có tọa độ là:

Viết phương trình mặt phẳng $\left( P \right)$  song song với mặt phẳng $\left( Q \right):x + y - z - 2 = 0$  và cách $\left( Q \right)$  một khoảng là \(2\sqrt 3 \) .

Trong không gian với hệ tọa độ \(Oxyz\), cho hai đường thẳng

\({d_1}:\left\{ \begin{array}{l}x = t\\y =  - 1 - 4t\\z = 6 + 6t\end{array} \right.\) và \(\,{d_2}:\dfrac{x}{2} = \dfrac{{y - 1}}{1} = \dfrac{{z + 2}}{{ - 5}}\).

Trong các phương trình sau đây, phương trình nào là phương trình của đường thẳng \({d_3}\) qua \(M\left( {1; - 1;2} \right)\) và vuông góc với cả \({d_1},\,\,{d_2}.\)

Cho hai điểm \(A\left( {1; - 2;0} \right),B\left( {0;1;1} \right)\), độ dài đường cao \(OH\) của tam giác \(OAB\) là:

Trong không gian với hệ tọa độ \(Oxyz\), cho đường thẳng \(\Delta :\left\{ {\begin{array}{*{20}{c}}{x = t{\rm{      }}}\\{y = 8 + 4t}\\{z = 3 + 2t}\end{array}} \right.\) và mặt phẳng $\left( P \right):x + y + z - 7 = 0.$ Phương trình đường thẳng \(\Delta '\) là hình chiếu vuông góc của \(\Delta \) trên \(\left( P \right)\) là:

Trong không gian với hệ tọa độ $Oxyz$, phương trình nào dưới đây là phương trình mặt cầu đi qua ba điểm $M\left( {2;3;3} \right),{\rm{ }}N\left( {2; - 1; - 1} \right),{\rm{ }}P\left( { - 2; - 1;3} \right)$ và có tâm thuộc mặt phẳng \((\alpha ):2x + 3y - z + 2 = 0\).

Mặt cầu $\left( S \right)$ có tâm \(I( - 1;2; - 5)\) cắt mặt phẳng \(\left( P \right):2x - 2y - z + 10 = 0\) theo thiết diện là hình tròn có diện tích \(3\pi \). Phương trình của $\left( S \right)$ là:

Cho \(y=f(x)\) là hàm số chẵn và liên tục trên \(\mathbb{R}.\) Biết \(\int\limits_{0}^{1}{f(x)\text{d}x=}\frac{1}{2}\int\limits_{1}^{2}{f(x)\text{d}x}=1.\) Giá trị của \(\int\limits_{-2}^{2}{\frac{f(x)}{{{3}^{x}}+1}\text{d}x}\) bằng

 Tìm thể tích \(V\) của vật tròn xoay sinh ra bởi đường tròn \({{x}^{2}}+{{\left( y-3 \right)}^{2}}=4\) khi quay quanh trục \(Ox.\)

Cho số phức $z$ thỏa mãn $\left| {z - 2} \right| = 2$. Biết rằng tập hợp các điểm biểu diễn các số phức $w = \left( {1 - i} \right)z + i$ là một đường tròn. Tính bán kính $r$ của đường tròn đó

Trong không gian với hệ tọa độ \(Oxyz\), cho đường thẳng \(d:\dfrac{{x - 3}}{1} = \dfrac{{y - 3}}{3} = \dfrac{z}{2}\), mặt phẳng \(\left( \alpha  \right):x + y - z + 3 = 0\) và điểm \(A\left( {1;2 - 1} \right)\). Đường thẳng \(\Delta \) đi qua \(A\) cắt \(d\) và song song với mặt phẳng \(\left( \alpha  \right)\) có phương trình là:

Gọi \(F\left( x \right) = \left( {a{x^3} + b{x^2} + cx + d} \right){e^x}\) là một nguyên hàm của hàm số \(f\left( x \right) = \left( {2{x^3} + 9{x^2} - 2x + 5} \right){e^x}\). Tính \({a^2} + {b^2} + {c^2} + {d^2}\)

Cho điểm $A(0 ; 8 ; 2)$ và mặt cầu $(S)$ có phương trình \((S):{\left( {x - 5} \right)^2} + {\left( {y + 3} \right)^2} + {\left( {z - 7} \right)^2} = 72\) và điểm $B(1 ; 1 ; -9)$. Viết phương trình mặt phẳng $(P)$ qua $A$ tiếp xúc với $(S)$ sao cho khoảng cách từ $B$ đến $(P)$ là lớn nhất. Giả sử \(\overrightarrow n  = \left( {1;m;n} \right)\) là véctơ pháp tuyến của $(P)$. Lúc đó: