Kết quả:
0/25
Thời gian làm bài: 00:00:00
Cho hàm số $y = a{x^4} + b{x^2} + c\left( {a > 0} \right)$. Chọn kết luận đúng:
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên
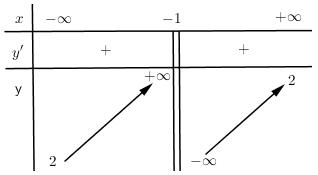
Tiệm cận đứng và tiệm cận ngang của đồ thị hàm số cắt nhau tại điểm có tọa độ là:
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
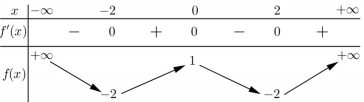
Số nghiệm thực của phương trình \(2f\left( x \right) + 3 = 0\) là:
Đường cong ở hình bên là đồ thị hàm số \(y=\dfrac{ax+2}{cx+b}\) với \(a,b,c\) là các số thực. Mệnh đề nào sau đây đúng?
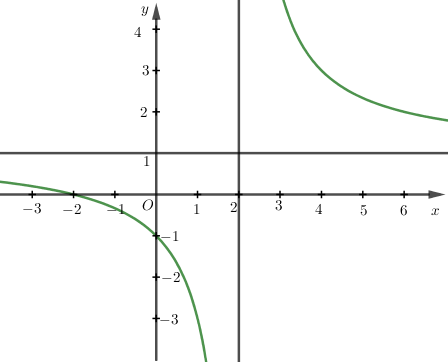
Cho hàm số \(f\left( x \right)\) có đạo hàm trên \(R\). Nếu hàm số \(f\left( x \right)\) nghịch biến trên \(R\) thì:
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = 1,\,\,\forall x \in \mathbb{R}\). Mệnh đề nào sau đây đúng?
Cho biết GTLN của hàm số $f\left( x \right)$ trên $\left[ {1;3} \right]$ là $M = - 2$. Chọn khẳng định đúng:
Giá trị lớn nhất của hàm số $f\left( x \right) = \dfrac{{\sin x}}{x}$ trên đoạn $\left[ {\dfrac{\pi }{6};\dfrac{\pi }{3}} \right]$ là:
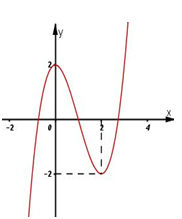
Hàm số $y = f\left( x \right) = a{x^3} + b{x^2} + cx + d$ có đồ thị như hình vẽ, chọn kết luận đúng:
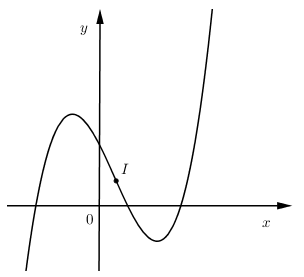
Hệ số góc của tiếp tuyến của đồ thị hàm số $y = \dfrac{{{x^4}}}{4} + \dfrac{{{x^2}}}{2} - 1$ tại điểm có hoành độ $x = - 1$ là:
Hàm số \(y = - {x^3} + {x^2} + 1\,\) xác định khi:
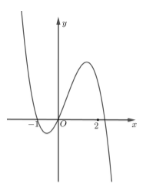
Cho hàm số y = f (x) có đồ thị như hình bên. Mệnh đề nào dưới đây đúng?
Tìm tất cả các giá trị của $m$ để hàm số $y = - \dfrac{1}{3}{x^3} + \dfrac{{m{x^2}}}{3} + 4$ đạt cực đại tại $x = 2?$
Tiệm cận ngang của đồ thị hàm số:
Hàm số nào dưới đây không có cực trị?
Gọi $m$ là giá trị nhỏ nhất của hàm số $y = x - 1 + \dfrac{4}{{x - 1}}$ trên khoảng $\left( {1; + \infty {\rm{\;}}} \right)$. Tìm $m?$
Tìm tất cả các giá trị thực của tham số $m$ để hàm số $y = mx - \sin x$ đồng biến trên $\mathbb{R}.$
Tìm $m$ để $({C_m})$ : $y = {x^4} - 2m{x^2} + 2$ có $3$ điểm cực trị là $3$ đỉnh của một tam giác vuông cân.
Biết rằng hàm số \(y = a{x^3} + b{x^2} + cx + d\,\,\left( {a\not = 0} \right)\) có đồ thị là một trong các dạng dưới đây:
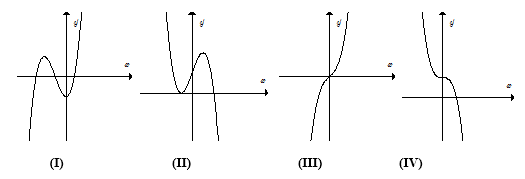
Mệnh đề nào sau đây là đúng?
Cho hàm số \(y = \dfrac{{2x + b}}{{cx + d}}\) có bảng biến thiên:
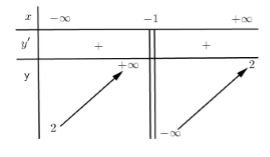
Giá trị của \(2{c^2} - 5{d^2}\) bằng
Cho hàm số \(y = {x^3} + 2m{x^2} + \left( {m + 3} \right)x + 4\,\,\,\left( {{C_m}} \right)\). Giá trị của tham số \(m\) để đường thẳng \(\left( d \right):y = x + 4\) cắt \(\left( {{C_m}} \right)\) tại ba điểm phân biệt \(A\left( {0;4} \right),\,\,B,\,\,C\) sao cho tam giác \(KBC\) có diện tích bằng \(8\sqrt 2 \) với điểm \(K\left( {1;3} \right)\) là:
Tiếp tuyến của đồ thị hàm số $y = \dfrac{{{x^3}}}{3} - 2{x^2} + x + 2$ song song với đường thẳng $y = - 2x + 5$ có phương trình là:
Cho hàm số \(f\left( x \right) = a{x^4} + b{x^3} + c{x^2} + dx + e,\) với \(a,b,c,d,e \in \mathbb{R}.\) Hàm số \(y = f'\left( x \right)\) có đồ thị như hình vẽ. Trong các khẳng định sau, khẳng định nào đúng?
Cho hai số thực \(x,\,y\) thỏa mãn \({x^2} + {y^2} - 4x + 6y + 4 + \sqrt {{y^2} + 6y + 10} = \sqrt {6 + 4x - {x^2}} \). Gọi \(M,\,m\) lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức \(T = \left| {\sqrt {{x^2} + {y^2}} - a} \right|\). Có bao nhiêu giá trị nguyên thuộc đoạn \(\left[ { - 10;\,10} \right]\) của tham số \(a\) để \(M \ge 2m\)?
Cho hàm số \(y = f\left( x \right) = {2^{2019}}{x^3} + {3.2^{2018}}{x^2} - 2018\) có đồ thị cắt trục hoành tại ba điểm phân biệt có hoành độ \({x_1};{x_2};{x_3}\). Tính giá trị biểu thức \(P = \dfrac{1}{{f'\left( {{x_1}} \right)}} + \dfrac{1}{{f'\left( {{x_2}} \right)}} + \dfrac{1}{{f'\left( {{x_3}} \right)}}.\)

