Đề kiểm tra học kì 2 - Đề số 5

Khoảng cách giữa hai đường thẳng ${d_1}:\dfrac{x}{2} = \dfrac{{y - 1}}{{ - 1}} = \dfrac{z}{3},{d_2}:\dfrac{{x + 1}}{1} = \dfrac{y}{3} = \dfrac{{z + 1}}{{ - 2}}$ là:

Cho hai điểm $A\left( { - 3;1;2} \right),B\left( {1;1;0} \right)$, tọa độ trung điểm đoạn thẳng $AB$  là:

Cho hai hàm số $y=f\left( x \right)$ và $y=g\left( x \right)$ liên tục trên đoạn $\left[ a;b \right].$ Gọi $D$ là hình phẳng giới hạn bởi đồ thị hàm số đó và các đường thẳng $x=a,\,\,x=b\,\,\,\left( a < b \right).$ Diện tích $S$ của hình phẳng $D$ được tính bởi công thức:

Giả sử ${z_1};{z_2}$ là hai nghiệm phức của phương trình: ${z^2} - 2z + 5 = 0$ và $A,B$ là các điểm biểu diễn của ${z_1};{z_2}$. Tọa độ trung điểm của đoạn thẳng $AB$ là

Trong không gian $Oxyz$, mặt phẳng $\left( {Oxy} \right)$ có phương trình là

Trong không gian với hệ tọa độ Oxyz, cho vectơ $\overrightarrow a  = \left( {2; - 2; - 4} \right)$; $\overrightarrow b  = \left( {1; - 1;1} \right)$. Mệnh đề nào dưới đây sai

Trong không gian $Oxyz$, điểm nào sau đây thuộc trục $Oy$?

Trong không gian tọa độ $Oxyz$, tính thể tích khối tứ diện $OBCD$ biết $B\left( {2;0;0} \right),C\left( {0;1;0} \right),D\left( {0;0; - 3} \right)$.

Gọi $A$ là điểm biểu diễn của số phức $z = 3 + 2i$ và $B$ là điểm biểu diễn của số phức $z' = 2 + 3i$. Mệnh đề nào sau đây là đúng?

Đổi biến $u = \ln x$ thì tích phân $I = \int\limits_1^e {\dfrac{{1 - \ln x}}{{{x^2}}}dx}$ thành:

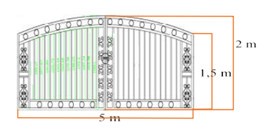
Ba Tí muốn làm cửa sắt được thiết kế như hình bên. Vòm cổng có hình dạng một parabol. Giá $1{m^2}$ cửa sắt là $660\,000$ đồng. Cửa sắt có giá (nghìn đồng) là:  

Cho $I = \int\limits_0^1 {\left( {2x - {m^2}} \right)dx}$. Có bao nhiêu giá trị nguyên dương m để $I + 3 \ge 0$?

Trong không gian với hệ tọa độ $Oxyz,$ cho mặt cầu $\left( S \right):{{\left( x-1 \right)}^{2}}+{{\left( y-2 \right)}^{2}}+{{\left( z-2 \right)}^{2}}=9$ và hai điểm $M\left( 4;-\,4;2 \right),\,\,N\left( 6;0;6 \right).$ Gọi $E$ là điểm thuộc mặt cầu $\left( S \right)$ sao cho $EM+EN$ đạt giá trị lớn nhất. Viết phương trình tiếp diện của mặt cầu $\left( S \right)$ tại $E.$

Để tính $I = \int\limits_0^{\dfrac{\pi }{2}} {{x^2}\,\cos x\,{\rm{d}}x}$ theo phương pháp tích phân từng phần, ta đặt

Trong không gian với hệ tọa độ $Oxyz$, mặt cầu $\left( S \right)$ có tâm $I\left( {1,2, - 3} \right)$ và đi qua điểm $A\left( {1,0,4} \right)$ có phương trình là

Hàm số $F\left( x \right) = {x^5} + 5{x^3} - x + 2$ là một nguyên hàm của hàm số nào sau đây? (C là hằng số).

Công thức tính độ dài véc tơ $\overrightarrow u  = \left( {a;b;c} \right)$ là:

Tìm nguyên hàm của hàm số $f\left( x \right) = {x^2}ln\left( {3x} \right)$

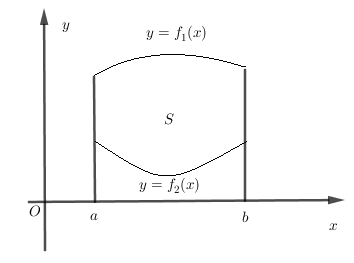
Cho hai hàm số $y = {f_1}\left( x \right)$ và $y = {f_2}\left( x \right)$ liên tục trên đoạn $\left[ {a;b} \right]$ và có đồ thị như hình vẽ bên. Gọi $S$ là hình phẳng giới hạn bởi hai đồ thị trên và các đường thẳng $x = a,x = b$. Thể tích $V$ của vật thể tròn xoay tạo thành khi quay $S$ quanh trục $Ox$ được tính bởi công thức nào sau đây ? 

Cho hai số phức $z = 3 - 4i$ và $z' = \left( {2 + m} \right) + mi\,\,\,\left( {m \in \mathbb{R}} \right)$ thỏa mãn $\left| {z'} \right| = \left| {iz} \right|$. Tổng tất cả các giá trị của m bằng

Đổi biến $x = 4\sin t$ của tích phân $I = \int\limits_0^{\sqrt 8 } {\sqrt {16 - {x^2}} dx}$ ta được:

Trong không gian tọa độ Oxyz, mặt cầu $\left( S \right):\,\,{{x}^{2}}+{{y}^{2}}+{{z}^{2}}-2x-4y-20=0$ và mặt phẳng $\left( \alpha  \right):\,\,x+2y-2z+7=0$ cắt nhau theo một đường tròn có chu vi bằng:

Véc tơ đơn vị trên trục $Ox$ là:

Trong không gian với hệ tọa độ Oxyz , để hai vecto $\overrightarrow a  = \left( {m;2;3} \right)$ và $\overrightarrow b \left( {1;n;2} \right)$  cùng phương thì $2m + 3n$ bằng.

Viết công thức tính thể tích $V$ của khối tròn xoay được tạo ra khi quay hình thang cong giới hạn bởi đồ thị hàm số $y = f\left( x \right)$, trục $Ox$ và hai đường thẳng $x = a,x = b\,\,\left( {a < b} \right)$ xung quanh trục $Ox?$

Cho hàm số $y = f\left( x \right)$ liên tục và nhận giá trị dương trên $\mathbb{R}.$ Gọi ${D_1}$ là hình phẳng giới hạn bởi đồ thị hàm số $y = f\left( x \right),$ các đường $x = 0,\,\,x = 1$ và trục $Ox.$ Gọi ${D_2}$ là hình phẳng giới hạn bởi đồ thị hàm số $y = \dfrac{1}{3}f\left( x \right),$ các đường $x = 0,\,\,\,x = 1$ và trục $Ox.$ Quay các hình phẳng ${D_1},\,\,{D_2}$ quanh trục $Ox$ ta được các khối tròn xoay có thể tích lần lượt là ${V_1},\,\,{V_2}.$

Khẳng định nào sau đâu là đúng?

Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d:$\left\{ \begin{array}{l}x = t\\y = 1 - t\\z = 2 + t\end{array} \right.$. Đường thẳng $d$ đi qua các điểm nào sau đây? 

Trong không gian với hệ tọa độ $Oxyz$, cho mặt phẳng $\left( P \right):2x - 2y + z - n = 0$ và đường thẳng $d:\left\{ \begin{array}{l}x = 1 + 2t\\y =  - 1 + t\\z = 3 + \left( {2m - 1} \right)t\end{array} \right.$. Với giá trị nào của $m,{\rm{ }}n$ thì $d$ song song $\left( P \right)$?

Cho các phát biểu sau: (Với $C$ là hằng số):

(I) $\int\limits_{}^{} {0dx}  = x + C$

(II) $\int\limits_{}^{} {\dfrac{1}{x}dx}  = \ln \left| x \right| + C$

(III) $\int\limits_{}^{} {\sin xdx}  =  - \cos x + C$

(IV) $\int\limits_{}^{} {\cot xdx}  =  - \dfrac{1}{{{{\sin }^2}x}} + C$

(V) $\int\limits_{}^{} {{e^x}dx}  = {e^x} + C$

(VI) $\int\limits_{}^{} {{x^n}dx}  = \dfrac{{{x^{n + 1}}}}{{n + 1}} + C\,\,\left( {\forall n \ne  - 1} \right)$

Số phát biểu đúng là:

Trong không gian với hệ tọa độ $Oxyz$, cho mặt cầu $\left( S \right):{x^2} + {y^2} + {z^2} - 2{\rm{x}} - 4y + 4{\rm{z}} - 16 = 0$ và đường thẳng $d:\dfrac{{x - 1}}{1} = \dfrac{{y + 3}}{2} = \dfrac{z}{2}$. Mặt phẳng nào trong các mặt phẳng sau chứa $d$ và tiếp xúc với mặt cầu $(S)$.

Cho $I = \int {\dfrac{{d{\rm{x}}}}{{\sqrt {2{\rm{x}} - 1}  + 4}}}  = \sqrt {2{\rm{x}} - 1}  - \ln {\left( {\sqrt {2{\rm{x}} - 1}  + 4} \right)^n} + C$ ở đó $n \in {\mathbb{N}^*}$. Giá trị biểu thức $S = \sin \dfrac{{n\pi }}{8}$ là:

Tính tích phân $I=\int\limits_{0}^{3}{\frac{\text{d}x}{x+2}}$. 

Tính tích phân $I = \int\limits_0^\pi  {{{\cos }^3}x\sin xdx}$

Biết $\int\limits_0^{\dfrac{\pi }{4}} {x.c{\rm{os}}2xdx}  = a + b\pi$, với $a,b$ là các số hữu tỉ. Tính $S = a + 2b$.     

 Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số $y={{x}^{2}}-4x+4$, trục tung, trục hoành. Giá trị của k để đường thẳng d đi qua $A(0;4)$ có hệ số góc k chia (H) thành 2 phần có diện tích bằng nhau là

Cho hình phẳng D giới hạn bởi đường cong $y={{\text{e}}^{x}}$, trục hoành và các đường thẳng $x=0,x=1$. Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích $V$ bằng bao nhiêu?

Tính môđun của số phức $z$ biết $\overline z  = \left( {4 - 3i} \right)\left( {1 + i} \right)$.

Gọi ${z_1},{z_2}$ là các nghiệm của phương trình: $z + \dfrac{1}{z} =  - 1$. Giá trị của $P = {z_1}^3 + {z_2}^3$ là:

Trên mặt phẳng tọa độ $Oxy$, tìm tập hợp các điểm biểu diễn các số phức $z$ thỏa mãn điều kiện $\left| {z - 2} \right| + \left| {z + 2} \right| = 10$.

Trong không gian với hệ tọa độ $Oxyz$, cho hai điểm  $A(0;2; - 1)$ , $B(2;0;1)$. Tìm tọa độ điểm $M$ nằm trên trục $Ox$ sao cho :$M{A^2} + M{B^2}$ đạt giá trị bé nhất.

Trong không gian Oxyz, phương trình mặt phẳng đi qua ba điểm $A\left( { - 3;0;0} \right);\,\,B\left( {0; - 2;0} \right);$ $C\left( {0;0;1} \right)$ được viết dưới dạng $ax + by - 6z + c = 0$. Giá trị của $T = a + b - c$ là :

Trong không gian Oxyz, gọi d là đường thẳng đi qua điểm $M\left( {2;1;1} \right)$, cắt và vuông góc với đường thẳng $\Delta :\dfrac{{x - 2}}{{ - 2}} = \dfrac{{y - 8}}{1} = \dfrac{z}{1}$. Tìm tọa độ giao điểm của d và mặt phẳng $\left( {Oyz} \right)$.

Trong không gian Oxyz, mặt cầu đi qua bốn điểm $A\left( {1;0;0} \right),$ $B\left( {0; - 2;0} \right),$ $C\left( {0;0;4} \right)$ và gốc tọa độ O có bán kính bằng

Trong không gian với hệ tọa độ $Oxyz$, cho hai điểm $A\left( {0; - 1;0} \right),B\left( {1;1; - 1} \right)$ và mặt cầu $(S):{x^2} + {y^2} + {z^2} - 2x + 4y - 2z - 3 = 0$. Mặt phẳng $(P)$ đi qua $A, B$ và cắt mặt cầu $(S)$ theo giao tuyến là đường tròn có bán kính lớn nhất có phương trình là:

Trong không gian với hệ tọa độ Oxyz cho ba điểm $A\left( {2;0;0} \right);\,\,B\left( {0;4;0} \right);\,\,C\left( {0;0;6} \right)$. Điểm M thay đổi trên mặt phẳng $\left( {ABC} \right)$ và điểm N là điểm trên tia OM sao cho $OM.ON = 12$. Biết rằng khi M thay đổi, điểm N luôn thuộc một mặt cầu cố định. Tìm bán kính của mặt cầu đó?

Trong không gian $Oxyz,$ cho mặt cầu $(S):{(x - 1)^2} + {(y - 2)^2} + {(z + 1)^2} = 6,$ tiếp xúc với hai mặt phẳng $(P):x + y + 2z\, + \,5 = 0,\,\,(Q):2x - y + z\, - \,5 = 0$ lần lượt tại các tiếp điểm $A,\,\,B.$ Độ dài đoạn thẳng $AB$ là

Cho tích phân $I = \int\limits_0^{\dfrac{\pi }{4}} {\dfrac{{{x^2}}}{{{{\left( {x\sin x + \cos x} \right)}^2}}}{\rm{d}}x}  = \dfrac{{m - \pi }}{{m + \pi }}$, giá trị của $m$ bằng :

Đặt $S$ là diện tích của hình phẳng giới hạn bởi đồ thị của hàm số $y = 4 - {x^2}$, trục hoành và đường thẳng $x =  - 2$, $x = m$, $\left( { - 2 < m < 2} \right)$. Tìm số giá trị của tham số $m$ để $S = \dfrac{{25}}{3}$.

Xét các số phức $z,\,\,w$ thỏa mãn $\left| z \right| = 2,\,\,\left| {iw - 2 + 5i} \right| = 1$. Giá trị nhỏ nhất của $\left| {{z^2} - wz - 4} \right|$ bằng:

Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng $\left( {{Q}_{1}} \right):\,\,3x-y+4z+2=0$ và $\left( {{Q}_{2}} \right):\,\,3x-y+4z+8=0$. Phương trình mặt phẳng (P) song song và cách đều hai mặt phẳng $\left( {{Q}_{1}} \right)$ và $\left( {{Q}_{2}} \right)$ là: