Câu hỏi:
2 năm trước
Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số \(y={{x}^{2}}-4x+4\), trục tung, trục hoành. Giá trị của k để đường thẳng d đi qua \(A(0;4)\) có hệ số góc k chia (H) thành 2 phần có diện tích bằng nhau là
Trả lời bởi giáo viên
Đáp án đúng: a
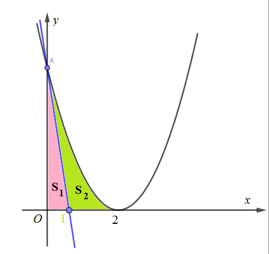
Phương trình đường thẳng d đi qua \(A(0;4)\) có hệ số góc k
\(y=k(x-0)+4\Leftrightarrow y=kx+4\)
Cho \(y=0\Rightarrow x=\frac{-4}{k},\,\,k\ne 0\). Vậy, d cắt Ox tại điểm \(I\left( -\frac{4}{k};0 \right)\).
Giao điểm của \(y={{x}^{2}}-4x+4\) và trục hoành: Cho \(y=0\Rightarrow x=2\).
\(\Rightarrow \) Để d chia (H) thành 2 phần thì \(0<\frac{-4}{k}<2\Leftrightarrow k<-2\).
Vì d chia (H) thành 2 phần có diện tích bằng nhau
\(\Rightarrow {{S}_{1}}={{S}_{2}}\Rightarrow {{S}_{1}}=\frac{1}{2}\left( {{S}_{1}}+{{S}_{2}} \right)\Leftrightarrow \int\limits_{0}^{-\frac{4}{k}}{\left| kx+4 \right|dx}=\frac{1}{2}\int\limits_{0}^{2}{\left| {{x}^{2}}-4x+4 \right|dx}\Leftrightarrow \int\limits_{0}^{-\frac{4}{k}}{(kx+4)dx}=\frac{1}{2}\int\limits_{0}^{2}{{{(x-2)}^{2}}dx}\)
\(\Leftrightarrow \left. \frac{{{(kx+4)}^{2}}}{2k} \right|_{0}^{-\frac{4}{k}}=\left. \frac{1}{2}.\frac{{{(x-2)}^{3}}}{3} \right|_{0}^{2}\Leftrightarrow -\frac{8}{k}=-\frac{1}{2}.\frac{{{(-2)}^{3}}}{3}\Leftrightarrow \frac{-8}{k}=\frac{4}{3}\Leftrightarrow k=-6\)
Hướng dẫn giải:
Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số \(y=f(x)\), trục hoành và hai đường thẳng \(x=a;\,\,x=b\) được tính theo công thức : \(S=\int\limits_{a}^{b}{\left| f(x) \right|dx}\)
