Đề kiểm tra học kì 2 - Đề số 1

Cho số phức $z$ thỏa mãn $\left( {1 + i} \right)z = 3-i$. Hỏi điểm biểu diễn của $z$ là điểm nào trong các điểm $M,N,P,Q$ ở hình bên ?

Hàm số nào dưới đây không có cực trị?

Công thức tính thể tích lăng trụ có diện tích đáy \(S\) và chiều cao \(h\) là:

Cho hàm số $f\left( x \right)$ liên tục trên $R$  và $\int\limits_{ - 2}^4 {f\left( x \right)} dx{\rm{ = 2}}$ . Mệnh đề nào sau đây là sai?

Cho hình \(\left( H \right)\) giới hạn bởi đường cong \(x = \sqrt y \), trục tung và hai đường thẳng \(y = 1,y = 4\). Thể tích khối tròn xoay tạo thành khi quay \(\left( H \right)\) quanh trục \(Oy\) được tính theo công thức:

Cho hàm số $f\left( x \right)$ xác định trên $\left[ {0;2} \right]$ và có GTNN trên đoạn đó bằng $5$. Chọn kết luận đúng:

Thể tích vật thể tròn xoay sinh ra khi quay hình phẳng giới hạn bới các đường \(x=\sqrt{y};\,y=-x+2,x=0\) quanh trục $Ox$ có giá trị là kết quả nào sau đây ?

Diện tích hình phẳng giới hạn bởi các đồ thị hàm số $y = {x^3} - x;y = 2x$ và các đường thẳng $x =  - 1;x = 1$ được xác định bởi công thức:

Diện tích xung quanh hình nón có bán kính đáy \(r = 3cm\) và độ dài đường sinh \(4cm\) là:

Cho hai hàm số \(f,\,\,g\) liên tục trên đoạn $\left[ {a;b} \right]$ và số thực $k$ tùy ý. Trong các khẳng định sau, khẳng định nào sai ?

Hãy chọn cụm từ (hoặc từ) cho dưới đây để sau khi điền nó vào chỗ trống mệnh đề sau trở thành mệnh đề đúng:

“Số cạnh của một hình đa diện luôn……………….số mặt của hình đa diện ấy”

Khoảng cách từ điểm \(M\left( {2;0;1} \right)\) đến đường thẳng $\Delta :\dfrac{{x - 1}}{1} = \dfrac{y}{2} = \dfrac{{z - 2}}{1}$ là:

Cho ${\left( {\sqrt 2  - 1} \right)^m} < {\left( {\sqrt 2  - 1} \right)^n}$. Khẳng định nào dưới đây đúng?

Cho $2$ số phức,\({z_1} = 1 + 3i,{\overline z _2} = 4 + 2i\). Tính môđun của số phức ${z_2} - 2{z_1}$

Giá trị của $x$ thỏa mãn \({\log _{\frac{1}{2}}}(3 - x) = 2\) là

Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như sau:

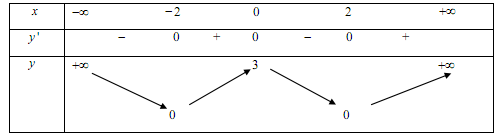
Khẳng định nào sau đây là khẳng định sai:

Điểm \(M\left( {x;y;z} \right)\) nếu và chỉ nếu:

Cho phương trình \({z^2} - 2z + 2 = 0\) . Mệnh đề nào sau đây là sai?

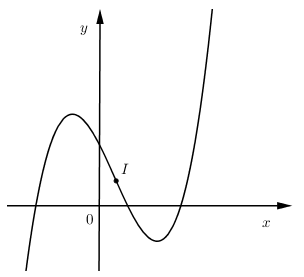
Hàm số $y = f\left( x \right) = a{x^3} + b{x^2} + cx + d$ có đồ thị như hình vẽ, chọn kết luận đúng:

Hàm số $y = \sin x$ là một nguyên hàm của hàm số nào trong các hàm số sau?

Nếu đặt $\left\{ \begin{array}{l}u = \ln \left( {x + 2} \right)\\{\rm{d}}v = x\,{\rm{d}}x\end{array} \right.$ thì tích phân $I = \int\limits_0^1 {x.\ln \left( {x + 2} \right){\rm{d}}x} $ trở thành

Trong không gian với hệ tọa độ \(Oxyz\), cho đường thẳng \(d:\left\{ \begin{array}{l}x = 1\\y = 2 + 3t\\z = 5 - t\end{array} \right.\left( {t \in R} \right)\). Vectơ nào dưới đây là vectơ chỉ phương của \(d\)?

Trong không gian $Oxyz$ cho ba vecto \(\vec a = \left( { - 1;1;0} \right),\vec b = \left( {1;1;0} \right),\vec c = \left( {1;1;1} \right)\). Mệnh đề nào dưới đây sai?

Trong không gian với hệ tọa độ $Oxyz$, cho mặt cầu $\left( S \right):{x^2} + {y^2} + {z^2} - 2{\rm{x  +  4y  -  4z  -  m  =  0}}$ có bán kính $R = 5$. Tìm giá trị của $m$?

Cho hình chóp tam giác đều $S.ABC$ có cạnh đáy bằng $a$, góc giữa cạnh bên và mặt đáy bằng \({60^0}\). Tính thể tích khối chóp $S.ABC$?

Gọi \(G\left( {4; - 1;3} \right)\) là tọa độ trọng tâm tam giác \(ABC\) với \(A\left( {0;2; - 1} \right),B\left( { - 1;3;2} \right)\). Tìm tọa độ điểm \(C\).

Cho hàm số $y = \dfrac{{x - 2}}{{{x^2} - 2x + m}}\left( C \right).$ Tất cả các giá trị của m để (C) có 3 đường tiệm cận là:

Tìm tất cả các giá trị của tham số $m$ để đường thẳng $y =  - 2x + m$ cắt đồ thị $(H)$ của hàm số $y = \dfrac{{2x + 3}}{{x + 2}}$ tại hai điểm$A,{\text{ }}B$ phân biệt sao cho $P = k_1^{2018} + k_2^{2018}$ đạt giá trị nhỏ nhất (với ${k_1},{k_2}$ là hệ số góc của tiếp tuyến tại $A,{\text{ }}B$ của đồ thị $(H)$.

Anh A mua 1 chiếc Laptop giá $23$ triệu đồng theo hình thức trả góp, lãi suất mỗi tháng là $0,5\% $. Hỏi mỗi tháng anh A phải trả cho cửa hàng bao nhiêu tiền để sau $6$ tháng anh trả hết nợ?

Đặt \(a = {\log _2}5\) và \(b = {\log _2}6\). Hãy biểu diễn \({\log _3}90\) theo $a$ và $b$?

Cho hàm số $f\left( x \right) = \dfrac{{{3^x}}}{{{7^{{x^2} - 4}}}}$. Hỏi khẳng định nào sau đây là sai?

Ta có \(\int {{x^2}.{e^x}dx = \left( {{x^2} + mx + n} \right)} {e^x} + C\) khi đó \(m.n\) bằng.

Tìm các số thực \(a,\,\,b\) để hàm số \(f\left( x \right)=a\cos \left( \frac{\pi x}{2} \right)+b\) thỏa mãn \(f\left( 1 \right)=1\) và \(\int\limits_{0}^{3}{f\left( x \right)\,\text{d}x}=5.\)

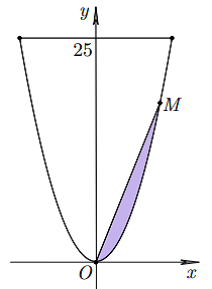
Ông B có một khu vườn giới hạn bởi đường parabol và một đường thẳng. Nếu đặt trong hệ tọa độ $Oxy$ như hình vẽ bên thì parabol có phương trình $y = {x^2}$và đường thẳng là $y = 25$. Ông B dự định dùng một mảnh vườn nhỏ được chia từ khu vườn bởi đường thẳng đi qua $O$ và điểm $M$ trên parabol để trồng hoa. Hãy giúp ông B xác định điểm $M$ bằng cách tính độ dài $OM$ để diện tích mảnh vường nhỏ bằng $\dfrac{9}{2}$.

Cho ba điểm $A,B,C$ lần lượt biểu diễn các số phức sau \({z_1} = 1 + i;\,{z_2} = {z_1}^2;\,{z_3} = m - i\). Tìm các giá trị thực của $m$ sao cho tam giác $ABC$ vuông tại $B$.

Trong số các số phức $z$ thỏa mãn điều kiện \(\left| {z - 4 + 3i} \right| = 3\), gọi ${z_0}$ là số phức có mô đun lớn nhất. Khi đó \(\left| {{z_0}} \right|\) là

Cho hình lăng trụ $ABC.A’B’C’$ có độ dài tất cả các cạnh bằng $a$ và hình chiếu vuông góc của đỉnh $C$ trên $(ABB’A’)$ là tâm của hình bình hành $ABB’A’$. Thể tích của khối lăng trụ là:

Cho hình chóp $S.ABC$ có $SA \bot (ABC);AC = b,AB = c,\widehat {BAC} = \alpha $. Gọi $B',C'$ lần lượt là hình chiếu vuông góc của $A$ lên $SB,SC$. Tính bán kính mặt cầu ngoại tiếp khối chóp $A.{\rm{ }}BCC'B'$ theo $b,c,\alpha $

Trong không gian với hệ tọa độ \(Oxyz,\) cho điểm \(M\left( 1;2;3 \right).\) Mặt phẳng \(\left( P \right)\) đi qua M và cắt các tia \(Ox;\,\,Oy;\,\,Oz\) lần lượt tại các điểm \(A;\,\,B;\,\,C\) \(\left( A;\,\,B;\,\,C\ne O \right)\) sao cho thể tích của tứ diện \(OABC\) nhỏ nhất. Phương trình của mặt phẳng \(\left( P \right)\) là

Trong không gian với hệ tọa độ $Oxyz$, cho mặt phẳng \((P):x - y - z - 1 = 0\) và đường thẳng $d:\dfrac{{x + 1}}{2} = \dfrac{{y - 1}}{1} = \dfrac{{z - 2}}{3}$.   Phương trình đường thẳng \(\Delta \)  qua \(A(1;1; - 2)\) vuông góc với $d$ và song song với $(P)$ là:

Trong không gian với hệ tọa độ $Oxyz$, cho hai điểm $A\left( {0; - 1;0} \right),B\left( {1;1; - 1} \right)$ và mặt cầu $(S):{x^2} + {y^2} + {z^2} - 2x + 4y - 2z - 3 = 0$. Mặt phẳng $(P)$ đi qua $A, B$ và cắt mặt cầu $(S)$ theo giao tuyến là đường tròn có bán kính lớn nhất có phương trình là:

Trong không gian với hệ tọa độ $Oxyz$, cho mặt cầu $(S)$ có phương trình: \({x^2} + {y^2} + {z^2} - 2x + 4y - 2z - 3 = 0\) và đường thẳng \(\Delta :\,\,\dfrac{x}{2} = \dfrac{{y + 1}}{{ - 2}} = z\) . Mặt phẳng $(P)$ vuông góc với \(\Delta \) và tiếp xúc với $(S)$ có phương trình là 

Cho parabol $\left( P \right):y = {x^2} + 1$  và đường thẳng $\left( d \right):y = mx + 2$. Biết rằng tồn tại $m$ để diện tích hình phẳng giới hạn bới $\left( P \right)$  và $\left( d \right)$  đạt giá trị nhỏ nhất, tính diện tích nhỏ nhất đó.

Trong không gian với hệ tọa độ $Oxyz$, cho ba vectơ $\vec a = \left( {1;m;2} \right),\vec b = \left( {m + 1;2;1} \right)$ và \(\vec c = \left( {0;m - 2;2} \right)\). Giá trị \(m\) bằng bao nhiêu để ba vectơ \(\vec a,\vec b,\vec c\) đồng phẳng

Tìm họ nguyên hàm của hàm số $f(x) = {\tan ^5}x$.

Cho tứ diện đều $ABCD$ có cạnh bằng $8$. Ở bốn đỉnh tứ diện, nguời ta cắt đi các tứ diện đều bằng nhau có cạnh bằng $x$, biết khối đa diện tạo thành sau khi cắt có thể tích bằng \(\dfrac{3}{4}\) thể tích tứ diện $ABCD$. Giá trị của $x$ là:

Xét số phức \(z\) thỏa mãn \(\left| {z + 2 - i} \right| + \left| {z - 4 - 7i} \right| = 6\sqrt 2 \). Gọi \(m,M\) lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của \(\left| {z - 1 + i} \right|\). Tính \(P = m + M\).

Cho các hàm số $y = f (x), y = g (x), y = \dfrac{{f\left( x \right) + 3}}{{g\left( x \right) + 1}}$ . Hệ số góc của các tiếp tuyến của đồ thị các hàm số đã cho tại điểm có hoành độ $x = 1$ bằng nhau và khác $0$. Khẳng định nào dưới đây là khẳng định đúng?

Số nghiệm của phương trình ${\log _3}\left| {{x^2} - \sqrt 2 x} \right| = {\log _5}\left( {{x^2} - \sqrt 2 x + 2} \right)$là

Cho điểm $A(0 ; 8 ; 2)$ và mặt cầu $(S)$ có phương trình \((S):{\left( {x - 5} \right)^2} + {\left( {y + 3} \right)^2} + {\left( {z - 7} \right)^2} = 72\) và điểm $B(1 ; 1 ; -9)$. Viết phương trình mặt phẳng $(P)$ qua $A$ tiếp xúc với $(S)$ sao cho khoảng cách từ $B$ đến $(P)$ là lớn nhất. Giả sử \(\overrightarrow n  = \left( {1;m;n} \right)\) là véctơ pháp tuyến của $(P)$. Lúc đó: