Câu hỏi:
3 năm trước
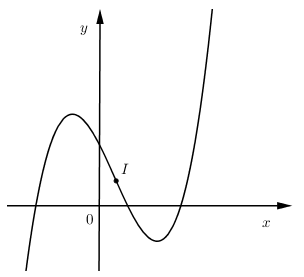
Hàm số $y = f\left( x \right) = a{x^3} + b{x^2} + cx + d$ có đồ thị như hình vẽ, chọn kết luận đúng:
Trả lời bởi giáo viên
Đáp án đúng: a
Quan sát đồ thị ta thấy $\mathop {\lim }\limits_{x \to + \infty } y = + \infty ;\mathop {\lim }\limits_{x \to - \infty } y = - \infty $ nên $a > 0$.


