Đề kiểm tra học kì 2 - Đề số 2

 Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số $y={{x}^{2}}-4x+4$, trục tung và trục hoành. Xác định k để đường thẳng (d) đi qua điểm $A\left( 0;4 \right)$ và có hệ số góc k chia (H) thành hai phần có diện tích bằng nhau.

Trong không gian với hệ tọa độ $Oxyz$, cho ba điểm

$A\left( {1;2; - 1} \right),{\rm{ }}B\left( {2;1;1} \right),{\rm{ }}C\left( {0;1;2} \right)$. Gọi $H\left( {a;b;c} \right)$ là trực tâm của tam giác $ABC$. Giá trị của $a + b + c$ bằng:

Tìm phần ảo $b$ của số phức $w = \dfrac{1}{{2i}}\left( {z - \bar z} \right)$ với $z = 5 - 3i$. 

Nguyên hàm của hàm số $f\left( x \right) = \sin x + \cos x$ là :

Trong không gian với hệ tọa độ $Oxyz$, cho mặt cầu $\left( S \right):{x^2} + {y^2} + {z^2} + 2x - 4y + 6z + 5 = 0$. Tiếp diện của $(S)$ tại điểm $M(-1;2;0)$ có phương trình là:

Cho hàm số $f\left( x \right)$ liên tục trên $R$ thỏa mãn $\int\limits_a^d {f\left( x \right)dx}  = 10;\int\limits_b^d {f\left( x \right)dx}  = 18;\int\limits_a^c {f\left( x \right)dx}  = 7$. Giá trị của $\int\limits_b^c {f\left( x \right)dx}$ là:

Cho số phức $z$ thỏa mãn$|z - 1 - 2i| = 4$. Gọi $M,m$ lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của $|z + 2 + i|$. Tính $S = {M^2} + {m^2}$.

Gọi $A$ là điểm biểu diễn của số phức $z = 3 + 2i$ và $B$ là điểm biểu diễn của số phức $z' = 2 + 3i$. Mệnh đề nào sau đây là đúng?

Cho hình phẳng $\left( H \right)$ giới hạn bởi các đường $y =  - \,{x^2} + 2x$ và $y = 0$. Tính thể tích của khối tròn xoay tạo thành khi quay hình $\left( H \right)$ quanh trục $Oy$ là

Trong không gian với hệ tọa độ $Oxyz$, cho điểm $M\left( {2; - 6;3} \right)$ và đường thẳng $d:\left\{ \begin{array}{l}x = 1 + 3t\\y =  - 2 - 2t\\z = t\end{array} \right.$. Tọa độ hình chiếu vuông góc của $M$ lên $d$ là:

Tính tổng $T$ của phần thực và phần ảo của số phức $z = {\left( {\sqrt 2  + 3i} \right)^2}.$

Cho ba điểm $A,{\rm{ }}B,{\rm{ }}C$ lần lượt biểu diễn ba số phức ${z_1},{\rm{ }}{z_2},{\rm{ }}{z_3}$ với ${z_3} \ne {z_1}$ và ${z_3} \ne {z_2}.$ Biết $\left| {{z_1}} \right| = \left| {{z_2}} \right| = \left| {{z_3}} \right|$ và ${z_1} + {z_2} = 0.$ Mệnh đề nào sau đây là đúng?

Cho phương trình $4{z^4} + m{z^2} + 4 = 0$ trong tập số phức và $m$ là tham số thực. Gọi ${z_1},{\rm{ }}{z_2},{\rm{ }}{z_3},{\rm{ }}{z_4}$ là bốn nghiệm của phương trình đã cho. Tìm tất cả các giá trị của $m$ để $\left( {z_1^2 + 4} \right)\left( {z_2^2 + 4} \right)\left( {z_3^2 + 4} \right)\left( {z_4^2 + 4} \right) = 324$.

Cho mặt phẳng $\left( P \right):x - y + z = 1,\left( Q \right):x + z + y - 2 = 0$ và điểm $M\left( {0;1;1} \right)$. Chọn kết luận đúng:

Trong không gian với hệ tọa độ vuông góc $Oxyz$, cho hai điểm $E\left( {2,1,1} \right),{\rm{ }}F\left( {0,3, - 1} \right)$. Mặt cầu $\left( S \right)$ đường kính $EF$ có phương trình là:

Gọi $S$ là tổng phần thực và phần ảo của số phức $w = {z^3} - i$, biết $z$ thỏa mãn $z + 2 - 4i = \left( {2 - i} \right)\overline {iz}$. Mệnh đề nào sau đây đúng?

Đổi biến $u = \ln x$ thì tích phân $I = \int\limits_1^e {\dfrac{{1 - \ln x}}{{{x^2}}}dx}$ thành:

Tọa độ giao điểm của đường thẳng d có phương trình $d:\dfrac{{x + 1}}{1} = \dfrac{y}{{ - 1}} = \dfrac{{z + 2}}{3}$ với mặt phẳng (P) có phương trình $(P):x + 2y - z - 3 = 0$ là:

Cho hình phẳng giới hạn bởi $D = \left\{ {y = \tan x;\,\,y = 0;\,\,x = 0;\,\,x = \dfrac{\pi }{3}} \right\}.$ Thể tích vật tròn xoay khi $D$ quay quanh trục $Ox$ là $V = \pi \left( {a - \dfrac{\pi }{b}} \right),$ với $a,\,\,b \in R.$ Tính $T = {a^2} + 2b.$

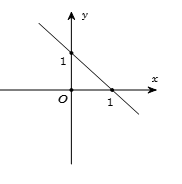
Tập hợp các điểm biểu diễn hình học của số phức $z$ là đường thẳng $\Delta$ như hình vẽ. Tìm giá trị nhỏ nhất của $\left| z \right|$.

Hoành độ điểm $M$ thỏa mãn $\overrightarrow {OM}  = 2\overrightarrow j  - \overrightarrow i  + \overrightarrow k$ là:

Cho hai véc tơ $\overrightarrow u  = \left( {m;2;1} \right)$ và $\overrightarrow v  = \left( {0;n;p} \right)$. Biết $\overrightarrow u  = \overrightarrow v$, giá trị $T = m - n + p$ bằng:

Trong không gian Oxyz, cho các điểm $A\left( 2;-2;\ 1 \right),\ B\left( 1;-1;\ 3 \right).$ Tọa độ của vecto $\overrightarrow{AB}$ là

Trong không gian với hệ tọa độ $Oxyz$ cho mặt phẳng $(\alpha ):4x + 3y - 7z + 3 = 0$ và điểm $I(0;1;1)$. Phương trình mặt phẳng $(\beta )$ đối xứng với $(\alpha )$ qua $I$ là:

Cho hai số phức ${z_1} = 2017 - i$ và ${z_2} = 2 - 2016i$. Tìm số phức $z = {z_1}.{z_2}.$

Viết  phương trình mặt cầu có tâm $I\left( { - 1;2;3} \right)$ và tiếp xúc với mặt phẳng $\left( P \right):2x - y - 2z + 1 = 0$

Cho số phức $z = 3-2i$. Tìm phần thực và phần ảo của số phức $\overline z$

Diện tích hình phẳng được giới hạn bởi đồ thị hàm số $y = x{e^x}$ , trục hoành, hai đường thẳng $x =  - 2;x = 3$ có công thức tính là

Cho hàm số $y=f\left( x \right)$ có $f'\left( x \right)=\frac{1}{x+1}$. Biết rằng $f\left( 0 \right)=2018$. Giá trị của biểu thức $f\left( 3 \right)-f\left( 1 \right)$  bằng:

Trong các hàm số dưới đây, hàm số nào có tích phân trên đoạn $[0;\pi ]$ đạt giá trị bằng $0$ ?

Tính tích phân $I = \int\limits_{\dfrac{\pi }{6}}^{\dfrac{\pi }{4}} {\dfrac{{\sin x - \cos x}}{{\sin x + \cos x}}dx}$

Cho tích phân $I = \int\limits_0^{\dfrac{\pi }{2}} {{e^x}\sin x}$. Gọi $a,b$ là các số nguyên thỏa mãn $I = \dfrac{{{e^{\dfrac{\pi }{2}}} + a}}{b}$. Chọn kết luận đúng:

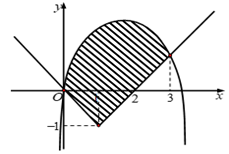
 Cho $\left( H \right)$ là hình phẳng được tô đậm trong hình vẽ và được giới hạn bởi các đường có phương trình $y=\frac{10}{3}x-{{x}^{2}}$, $y=\left\{ \begin{align} & -x\,\,\,\,\,\,\,\text{khi}\,x\le 1 \\ & x-2\,\,\text{khi}\,\,x>1 \\ \end{align} \right.$. Diện tích của $\left( H \right)$ bằng?

 Thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường $y=x{{e}^{x}},\ \ y=0,\ x=0,\ x=1$ xung quanh trục $Ox$ là:  

Tìm môđun của số phức $z$, biết $\dfrac{1}{{{z^2}}} = \dfrac{1}{2} + \dfrac{1}{2}i.$

Gọi ${z_{1,}}$${z_2}$ là các nghiệm phức của phương trình ${z^2} + 4z + 5 = 0$. Đặt $w = {\left( {1 + {z_1}} \right)^{100}} + {\left( {1 + {z_2}} \right)^{100}}$, khi đó

Cho ba điểm $A,B,C$ lần lượt biểu diễn các số phức sau ${z_1} = 1 + i;\,{z_2} = {z_1}^2;\,{z_3} = m - i$. Tìm các giá trị thực của $m$ sao cho tam giác $ABC$ vuông tại $B$.

Tập điểm biểu diễn số phức $z$ thỏa mãn ${\left| z \right|^2} = {z^2}$ là:

Cho ${z_1},{z_2}$ thỏa mãn $|{z_1} - {z_2}| = 1$ và $|{z_1} + {z_2}| = 3$. Tính $\max T = |{z_1}| + |{z_2}|$ 

Trong không gian với hệ tọa độ $Oxyz$,  cho tứ diện $ABCD$  có $A(2; - 1;1)$, $B(3;0; - 1)$, $C(2; - 1;3)$ và $D$ thuộc trục $Oy$ . Tính tổng tung độ của các điểm $D$, biết thể tích tứ diện bằng $5$ .

Trong không gian với hệ tọa độ $Oxyz,$ cho các điểm $A\left( 0;1;2 \right),\,\,B\left( 2;-\,2;0 \right)$ và $C\left( -\,2;0;1 \right).$ Mặt phẳng $\left( P \right)$ đi qua $A,$ trực tâm $H$ của tam giác $ABC$ và vuông góc với mặt phẳng $\left( ABC \right)$ có phương trình là

Trong không gian với hệ tọa độ $Oxyz$, cho $d$ là đường thẳng đi qua gốc tọa độ $O$, vuông góc với trục $Ox$ và vuông góc với đường thẳng $\Delta :\left\{ \begin{array}{l}x = 1 + t\\y = 2 - t\\z = 1 - 3t\end{array} \right.$. Phương trình của $d$ là:

Cho hình lập phương $A\left( {0;0;0} \right),B\left( {1;0;0} \right),D\left( {0;1;0} \right),A'\left( {0;0;1} \right)$. Gọi $M,N$ lần lượt là trung điểm của $AB,CD$. Khoảng cách giữa $MN$ và $A'C$ là:

Trong không gian với hệ tọa độ $Oxyz,$ cho các điểm $A\left( -\,1;1;1 \right),\,\,B\left( 1;0;1 \right).$ Mặt phẳng $\left( P \right)$ đi qua $A,\,\,B$ và $\left( P \right)$ cách điểm $O$ một khoảng lớn nhất. Phương trình của mặt phẳng $\left( P \right)$ là

Trong không gian với hệ tọa độ $Oxyz$, cho hai điểm $A\left( {0; - 1;0} \right),B\left( {1;1; - 1} \right)$ và mặt cầu $(S):{x^2} + {y^2} + {z^2} - 2x + 4y - 2z - 3 = 0$. Mặt phẳng $(P)$ đi qua $A, B$ và cắt mặt cầu $(S)$ theo giao tuyến là đường tròn có bán kính lớn nhất có phương trình là:

Cho điểm $A(0 ; 8 ; 2)$ và mặt cầu $(S)$ có phương trình $(S):{\left( {x - 5} \right)^2} + {\left( {y + 3} \right)^2} + {\left( {z - 7} \right)^2} = 72$ và điểm $B(1 ; 1 ; -9)$. Viết phương trình mặt phẳng $(P)$ qua $A$ tiếp xúc với $(S)$ sao cho khoảng cách từ $B$ đến $(P)$ là lớn nhất. Giả sử $\overrightarrow n  = \left( {1;m;n} \right)$ là véctơ pháp tuyến của $(P)$. Lúc đó:

Cho hàm số $y=f(x)$ có $f'(x)$ liên tục trên nửa khoảng $\left[ 0;+\infty  \right)$ thỏa mãn $3f(x)+f'(x)=\sqrt{1+3{{e}^{-2x}}}$ biết $f(0)=\frac{11}{3}$. Giá trị $f\left( \frac{1}{2}\ln 6 \right)$ bằng

Người ta cần trồng hoa tại phần đắt nằm phía ngoài đường tròn tâm gốc tọa độ $O$ , bán kính bằng $\dfrac{1}{{\sqrt 2 }}$ và phía trong của Elip có độ dài trục lớn bằng $2\sqrt 2$ và độ dài trục nhỏ bằng $2$ (như hình vẽ bên). Trong mỗi một đơn vị diện tích cần bón $\dfrac{{100}}{{(2\sqrt 2  - 1)\pi }}kg$ phân hữu cơ. Hỏi cần sử dụng bao nhiêu kg phân hữu cơ để bón cho hoa?

Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng $\left( {{Q}_{1}} \right):\,\,3x-y+4z+2=0$ và $\left( {{Q}_{2}} \right):\,\,3x-y+4z+8=0$. Phương trình mặt phẳng (P) song song và cách đều hai mặt phẳng $\left( {{Q}_{1}} \right)$ và $\left( {{Q}_{2}} \right)$ là:

Trong không gian với hệ tọa độ $Oxyz$, cho mặt phẳng $\left( P \right):x + 2y = 0$. Phương trình nào sau đây là phương trình đường thẳng qua $A\left( { - 1;3; - 4} \right)$ cắt trục $Ox$ và song song với mặt phẳng $\left( P \right)$: