Cho ba điểm \(A,{\rm{ }}B,{\rm{ }}C\) lần lượt biểu diễn ba số phức \({z_1},{\rm{ }}{z_2},{\rm{ }}{z_3}\) với \({z_3} \ne {z_1}\) và \({z_3} \ne {z_2}.\) Biết \(\left| {{z_1}} \right| = \left| {{z_2}} \right| = \left| {{z_3}} \right|\) và \({z_1} + {z_2} = 0.\) Mệnh đề nào sau đây là đúng?
Trả lời bởi giáo viên
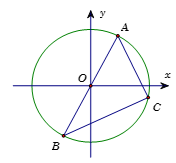
Giả sử \(\left| {{z_1}} \right| = \left| {{z_2}} \right| = \left| {{z_3}} \right| = R.\)
Khi đó \(A,{\rm{ }}B,{\rm{ }}C\) nằm trên đường tròn \(\left( {O;R} \right)\).
Do \({z_1} + {z_2} = 0\) nên hai điểm \(A,{\rm{ }}B\) đối xứng nhau qua \(O.\) Như vậy điểm \(C\) nằm trên đường tròn đường kính \(AB\) (bỏ đi hai điểm \(A\) và \(B\)) hay tam giác \(ABC\) vuông tại \(C\).
Hướng dẫn giải:
Biểu diễn hình học các điểm biểu diễn \({z_1},{z_2},{z_3}\) và nhận xét tam giác \(ABC\).

