Kết quả:
0/66
Thời gian làm bài: 00:00:00
Trong mặt phẳng tọa độ \(Oxy\), gọi \(A,B,C\) lần lượt là các điểm biểu diễn các số phức \({z_1},{z_2}\) , \({z_1} + {z_2}\). Xét các mệnh đề sau:
1) \(\left| {{z_1}} \right| = \left| {{z_2}} \right| \Leftrightarrow \left[ \begin{array}{l}{z_1} = {z_2}\\{z_1} = - {z_2}\end{array} \right.\).
2) \(\left| {{z_1} + {z_2}} \right| \le \left| {{z_1}} \right| + \left| {{z_2}} \right|\).
3) Nếu \(\overrightarrow {OA} .\overrightarrow {OB} = 0\) thì \({z_1}.\overline {{z_2}} + {z_2}.\overline {{z_1}} = 0\).
4) \(O{C^2} + A{B^2} = 2\left( {O{A^2} + O{B^2}} \right)\).
Trong các mệnh đề trên có bao nhiêu mệnh đề đúng?
Tìm số hạng không chứa x trong khai triển \({\left( {{x^2} - \dfrac{2}{x}} \right)^{15}}\).
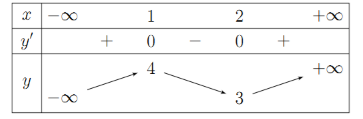
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình vẽ
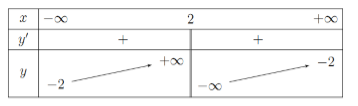
Tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là:
Cho hàm số \(y = {x^4} - 1\) có đồ thị \(\left( C \right)\). Tiếp tuyến của đồ thị \(\left( C \right)\) tại điểm với hoành độ bằng 0 có hệ số góc là
Cho hình lập phương \(ABCD.A'B'C'D'\) có thể tích bằng \(8{a^3}\). Khi đó độ dài cạnh hình lập phương đã cho bằng
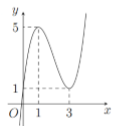
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ bên. Hàm số \(y = f\left( x \right)\) nghịch biến trên khoảng nào trong các khoảng sau?
Diện tích của mặt cầu bán kính \(R = 3\) bằng
Trong không gian \(Oxyz\), hình chiếu của điểm \(M\left( {2;3; - 2} \right)\) trên trục \(Oy\) có tọa độ là:
Trong các số phức \({z_1} = - 2i,\,\,{z_2} = 2 - i,\,\,{z_3} = 5i,\,\,{z_4} = 4\) có bao nhiêu số thuần ảo?
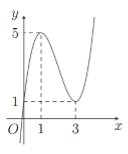
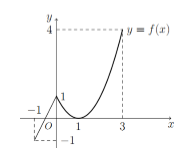
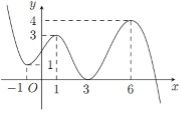
Cho hàm số bậc ba \(y = f\left( x \right)\) có đồ thị như hình vẽ bên. Số nghiệm của phương trình \(f\left( x \right) = 3\) là:
Tập nghiệm của phương trình \({\log _2}\left( {\dfrac{1}{x}} \right) = {\log _{\dfrac{1}{2}}}\left( {{x^2} - x - 1} \right)\) là
Cho \(\int\limits_0^1 {f\left( x \right)} dx = - 2\) và \(\int\limits_1^5 {\left( {2.f\left( x \right)} \right)} dx = 6\), khi đó \(\int\limits_0^5 {f\left( x \right)} dx\) bằng
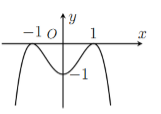
Đường cong trong hình bên là đồ thị của hàm số nào dưới đây?
Họ nguyên hàm của hàm số \(f\left( x \right) = 3{x^2} + \dfrac{1}{{{{\cos }^2}x}}\) là
Gọi \({z_1},{z_2}\) là hai nghiệm phức của phương trình \(2{z^2} - z + 7 = 0\). Tính \(S = \left| {{z_1}.\overline {{z_2}} + {z_2}.\overline {{z_1}} } \right|\).
Tìm phần ảo của số phức \(z\), biết \(\left( {2 - i} \right)z = 1 + 3i\).
Hình nón \(\left( {\rm N} \right)\) có thiết diện qua trục là tam giác đều có cạnh bằng 4. Diện tích toàn phần của \(\left( {\rm N} \right)\) bằng
Cho cấp số nhân \(\left( {{u_n}} \right)\) có hai số hạng đầu tiên là \({u_1} = - 3\) và \({u_2} = 9\). Công bội của cấp số nhân đã cho bằng
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\left[ { - 1;3} \right]\) và có đồ thị như hình vẽ bên. Gọi \(M,\,m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = f\left( x \right)\) trên đoạn \(\left[ { - 1;3} \right]\). Tính \(M - m\).
Hình phẳng được giới hạn bởi các đường tiệm cận của đồ thị hàm số \(y = \dfrac{{2x - 3}}{{x + 1}}\) và hai trục tọa độ có diện tích bằng
Cho hàm số \(\left[ { - 1;3} \right]\) có bảng biến thiên như hình vẽ dưới đây. Hàm số đạt cực tiểu tại điểm nào trong các điểm sau?
Tìm tập xác định \(D\) của hàm số \(y = {\left( {4 - {x^2}} \right)^{\dfrac{1}{5}}}\).
Trong không gian \(Oxyz\), cho mặt cầu \(\left( S \right):{x^2} + {y^2} + {z^2} - 2x + 4y - 6z - 11 = 0\). Tọa độ tâm của mặt cầu là \(I\left( {a;b;c} \right)\). Tính \(a + b + c\).
Trong không gian \(Oxyz\), cho mặt phẳng \(\left( P \right):x + 2y + 3 = 0\). Đường thẳng \(\Delta \) qua \(A\left( {1;2; - 3} \right)\) vuông góc với mặt phẳng \(\left( P \right)\) có phương trình là
Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \(a\), cạnh bên \(SD = \dfrac{{a\sqrt {17} }}{2}\). Hình chiếu vuông góc của \(S\) lên mặt phẳng \(\left( {ABCD} \right)\) là trung điểm \(H\) của đoạn thẳng \(AB\). Gọi \(E\) là trung điểm của \(AD\). Tính khoảng cách giữa hai đường thẳng \(HE\) và \(SB\).
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ bên. Tính tích phân \(I = \int\limits_{ - 1}^3 {f\left( {2x - 1} \right)dx} \).
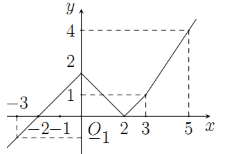
Cho hình chóp tứ giác đều \(S.ABCD\) có cạnh đáy bằng \(a\), góc giữa mặt bên và mặt đáy bằng \({60^0}\). Gọi O là giao điểm của AC và BD. Tính khoảng cách từ O đến mặt phẳng \(\left( {SAB} \right)\).
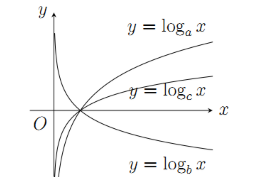
Cho các hàm số có đồ thị như hình vẽ bên. Mệnh đề nào sau đây đúng?
Trong không gian \(Oxyz\), cho mặt cầu \(\left( S \right):{x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0\), với \(a,b,c\) đều là các số thực dương. Biết mặt cầu \(\left( S \right)\) cắt 3 mặt phẳng tọa độ \(\left( {Oxy} \right),\left( {Oxz} \right),\left( {Oyz} \right)\) theo các giao tuyến là các đường tròn có bán kính bằng \(\sqrt {13} \) và mặt cầu \(\left( S \right)\) đi qua \(M\left( {2;0;1} \right)\). Tính \(a + b + c\)
Tìm tham số \(m\) để hàm số \(y = \dfrac{{{{\log }_{\dfrac{1}{2}}}x - 2}}{{{{\log }_2}x - m}}\) đồng biến trên khoảng \(\left( {0;1} \right)\).
Cho hàm số \(f\left( x \right) = \ln \left( {{e^x} + \pi m} \right)\) thỏa mãn \(f'\left( {\ln 3} \right) = 3\). Mệnh đề nào sau đây đúng?
Trong không gian \(Oxyz\), cho đường thẳng \({d_1}:\left\{ \begin{array}{l}x = 1 + t\\y = 2 + t\\z = 3\end{array} \right.\) và \({d_2}:\left\{ \begin{array}{l}x = 1\\y = 2 + 7t\\z = 3 + t\end{array} \right.\). Phương trình đường phân giác của góc nhọn giữa \({d_1}\) và \({d_2}\) là:
Trong không gian \(Oxyz\), cho đường thẳng \(d:\dfrac{x}{{ - 1}} = \dfrac{{y + 1}}{2} = \dfrac{{z - 2}}{1}\) và mặt phẳng \(\left( P \right)\) có phương trình \(2x - y - 2z + 4 = 0\). Mặt phẳng chứa đường thẳng \(d\) và tạo với mặt phẳng \(\left( P \right)\) góc với số đo nhỏ nhất có phương trình là:
Cho số phức \(z\) thỏa mãn \(2\left| z \right| = \left| {{z^2} + 4} \right|\). Tìm giá trị lớn nhất của \(\left| z \right|\).
Một hộp đựng 20 viên bi khác nhau được đánh số từ 1 đến 20. Lấy ba viên bi từ hộp trên rồi cộng số ghi trên đó lại. Hỏi có bao nhiêu cách để lấy kết quả thu được là một số chia hết cho 3?
Tìm tham số m để tổng các nghiệm của phương trình sau đạt giá trị nhỏ nhất \(1 + \left[ {2{x^2} - m\left( {m + 1} \right)x - 2} \right]{.2^{1 + mx - {x^2}}} = \left( {{x^2} - mx - 1} \right){.2^{mx\left( {1 - m} \right)}} + {x^2} - {m^2}x\).
Có bao nhiêu số nguyên \(m \in \left[ { - 5;5} \right]\) để \(\mathop {\min }\limits_{\left[ {1;3} \right]} \left| {{x^3} - 3{x^2} + m} \right| \ge 2\).
Có bao nhiêu số nguyên \(m \in \left( { - 7;7} \right)\) để đồ thị hàm số \(y = \left| {{x^4} - 3m{x^2} - 4} \right|\) có đúng ba điểm cực trị \(A,B,C\) và diện tích tam giác \(ABC\) lớn hơn 4.
Cho \(0 \le x \le 2020\) và \({\log _2}\left( {2x + 2} \right) + x - 3y = {8^y}\). Có bao nhiêu cặp số \(\left( {x;y} \right)\) nguyên thỏa mãn các điều kiện trên?
Cho \(I = \int\limits_0^1 {\left( {x + \sqrt {{x^2} + 15} } \right)dx} = a + b\ln 3 + c\ln 5\) với \(a,b,c \in \mathbb{Q}\). Tính tổng \(a + b + c\).
Cho phương trình \({x^3} + \left( {m - 12} \right)\sqrt {4x - m} = 4x\left( {\sqrt {4x - m} - 3} \right)\), với \(m\) là tham số. Có bao nhiêu giá trị nguyên của m để phương trình đã cho có hai nghiệm thực phân biệt?
Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\) và bảng xét dấu của đạo hàm như hình vẽ sau

Có bao nhiêu số nguyên \(m \in \left( {0;2020} \right)\) để hàm số \(g\left( x \right) = f\left( {{x^2} - x + m} \right)\) nghịch biến trên khoảng \(\left( { - 1;0} \right)\)?
Mệnh đề nào sau đây sai?
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh bằng \(a\). Biết tam giác \(SBA\) vuông tại \(B\), tam giác \(SCA\) vuông tại \(C\) và khoảng cách giữa hai đường thẳng \(AC\) và \(SB\) bằng \(\dfrac{{3a}}{{\sqrt {13} }}\). Tính thể tích khối chóp \(S.ABC\).
Trong không gian \(Oxyz\), gọi \(\Delta \) là đường thẳng đi qua \(M\left( {0;0;2} \right)\) và song song với mặt phẳng \(\left( P \right):x + y + z + 3 = 0\) sao cho khoảng cách từ \(A\left( {5;0;0} \right)\) đến đường thẳng \(\Delta \) nhỏ nhất. Một vectơ chỉ phương của đường thẳng \(\Delta \) là
Tính thể tích của vật thể nằm giữa hai mặt phẳng \(x = - 1\) và \(x = 1\), biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục \(Ox\) có hoành độ \(x\left( { - 1 \le x \le 1} \right)\) là một tam giác vuông cân với cạnh huyền bằng \(\sqrt {1 - {x^4}} \).
Cho tứ diện gần đều \(ABCD\), biết \(AB = CD = 5,AC = BD = \sqrt {34} ,AD = BC = \sqrt {41} \). Tính sin của góc giữa hai đường thẳng \(AB\) và \(CD\).
Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) và đồ thị hàm số \(y = f\left( x \right)\) như hình vẽ bên. Tìm số điểm cực trị của hàm số \(y = {2019^{f\left( {f\left( x \right) - 1} \right)}}\).
Trong không gian \(Oxyz\), cho điểm \(S\left( { - 2;1; - 2} \right)\) nằm trên mặt cầu \(\left( S \right):{x^2} + {y^2} + {z^2} = 9\). Từ điểm \(S\) kẻ ba dây cung \(SA,SB,SC\) với mặt cầu \(\left( S \right)\) có độ dài bằng nhau và đôi một tạo với nhau góc \({60^0}\). Dây cung \(AB\) có độ dài bằng:
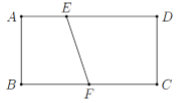
Có một miếng bìa hình chữ nhật \(ABCD\) với \(AB = 3\) và \(AD = 6\). Trên cạnh \(AD\) lấy điểm \(E\) sao cho \(AE = 2\), trên cạnh \(BC\) lấy điểm \(F\) là trung điểm của \(BC\). Cuốn miếng bìa lại sao cho \(AB\) trùng \(DC\)để tạo thành mặt xung quanh của một hình trụ.
Khi đó tính thể tích \(V\) của tứ diện \(ABEF\).
Mốc trắng dinh dưỡng bằng hình thức
Khi nói về mốc trắng, nhận định nào dưới đây là không chính xác ?
Chất kháng sinh pênixilin được sản xuất từ một loại
Cấu tạo nấm rơm gồm
Ở nấm, các phiến mỏng chứa rất nhiểu bào tử nằm ở
Loại nấm nào dưới đây được xếp vào nhóm nấm mũ ?
Nấm cần những điều kiện gì để phát triển ?
Nhiệt độ thích hợp nhất cho sự phát triển của nấm là
Nấm sinh sản chủ yếu theo hình thức nào ?
Đặc điểm chung của nấm là gì ?
Nấm không phải là thực vật vì:
Nấm khác tảo ở điểm nào ?
Loại nấm nào dưới đây được sử dụng làm thức ăn cho con người ?
Ở người, bệnh nào dưới đây do nấm gây ra ?
Loại nấm nào dưới đây thường gây hại trên cây ngô ?
Những loài nấm độc thường có điểm đặc trưng nào sau đây ?

