Câu hỏi:
2 năm trước
Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \(a\), cạnh bên \(SD = \dfrac{{a\sqrt {17} }}{2}\). Hình chiếu vuông góc của \(S\) lên mặt phẳng \(\left( {ABCD} \right)\) là trung điểm \(H\) của đoạn thẳng \(AB\). Gọi \(E\) là trung điểm của \(AD\). Tính khoảng cách giữa hai đường thẳng \(HE\) và \(SB\).
Trả lời bởi giáo viên
Đáp án đúng: d
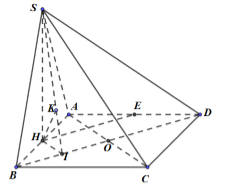
Ta có: \(HE//\left( {SBD} \right) \Rightarrow d\left( {HE;SB} \right) = d\left( {HE;\left( {SBD} \right)} \right) = d\left( {H;\left( {SBD} \right)} \right)\)
Gọi O là tâm của hình vuông, I là trung điểm của BO.
\( \Rightarrow HI//AC\), mà \(BD \bot AC \Rightarrow HI \bot BD\)
Mà \(SH \bot BD \Rightarrow BD \bot \left( {SHI} \right) \Rightarrow BD \bot HK\) \(\left( {K \in SI,\,\,HK \bot SI} \right)\)
\( \Rightarrow d\left( {H;\left( {SBD} \right)} \right) = HK\)
\(HD = \sqrt {{a^2} + \dfrac{{{a^2}}}{4}} = \dfrac{{a\sqrt 5 }}{2},\,\,SH = \sqrt {S{D^2} - H{D^2}} = \sqrt {\dfrac{{17{a^2}}}{4} - \dfrac{{5{a^2}}}{4}} = a\sqrt 3 \)
\(HI = \dfrac{1}{2}AO = \dfrac{1}{2}.\dfrac{{a\sqrt 2 }}{2} = \dfrac{{a\sqrt 2 }}{4}\)
\(\dfrac{1}{{H{K^2}}} = \dfrac{1}{{S{H^2}}} + \dfrac{1}{{H{I^2}}} \Leftrightarrow \dfrac{1}{{H{K^2}}} = \dfrac{1}{{3{a^2}}} + \dfrac{8}{{{a^2}}} = \dfrac{{25}}{{3{a^2}}} \Rightarrow HK = \dfrac{{a\sqrt 3 }}{5}\)
Vậy \(d\left( {HE;SB} \right) = \dfrac{{a\sqrt 3 }}{5}.\)
Hướng dẫn giải:
Chuyển từ tính khoảng cách giữa hai đường thẳng \( \to \) tính khoảng cách giữa đường thẳng và mặt phẳng song song \( \to \) tính khoảng cách từ điểm đến mặt phẳng.
Câu hỏi khác
- Đề thi thử THPTQG môn Toán Chuyên ĐH Vinh Nghệ An lần 3 Toán 12 có lời giải chi tiết
- Đề thi thử THPTQG - Đề số 2 Toán 12 có lời giải chi tiết
- Đề thi thử THPTQG - Đề số 4 Toán 12 có lời giải chi tiết
- Đề thi thử THPTQG - Đề số 1 Toán 12 có lời giải chi tiết
- Đề tập huấn thi THPTQG Sở Giáo Dục và Đào Tạo Bắc Ninh 2019 Toán 12 có lời giải chi tiết
