Trả lời bởi giáo viên
Đáp án đúng: b
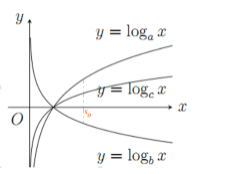
Nhận xét:
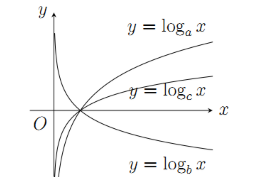
Hàm số \(y = {\log _a}x,\,\,y = {\log _c}x\) đồng biến trên \(\left( {0; + \infty } \right) \Rightarrow a;\,\,c > 1\)
Hàm số \(y = {\log _b}x\) nghịch biến trên \(\left( {0; + \infty } \right) \Rightarrow b < 1\)
Lấy \({x_0} > 1\) (như hình vẽ). Ta có: \({\log _a}{x_0} > {\log _c}{x_0} \Rightarrow a < c\)
\( \Rightarrow b < 1 < a < c \Leftrightarrow b < a < c.\)
Hướng dẫn giải:
Hàm số \(y = {\log _a}x\,\,\left( {x > 0} \right)\) đồng biến trên \(\left( {0; + \infty } \right)\) nếu \(a > 1\) và nghịch biến trên \(\left( {0; + \infty } \right)\) nếu \(0 < a < 1\).