Trong không gian \(Oxyz\), gọi \(\Delta \) là đường thẳng đi qua \(M\left( {0;0;2} \right)\) và song song với mặt phẳng \(\left( P \right):x + y + z + 3 = 0\) sao cho khoảng cách từ \(A\left( {5;0;0} \right)\) đến đường thẳng \(\Delta \) nhỏ nhất. Một vectơ chỉ phương của đường thẳng \(\Delta \) là
Trả lời bởi giáo viên
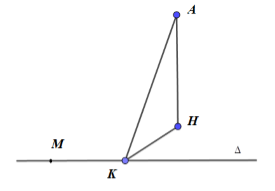
Do \(\Delta \) là đường thẳng đi qua \(M\left( {0;0;2} \right)\) và song song với mặt phẳng \(\left( P \right):x + y + z + 3 = 0\) \( \Rightarrow \Delta \subset \left( Q \right)\): qua M và song song \(\left( P \right)\).
Phương trình mặt phẳng (Q) là: \(x + y + z - 2 = 0\).
Dựng \(AH \bot \left( Q \right),AK \bot \Delta \). Ta có: \(AK \ge AH\). Do đó, khoảng cách từ \(A\left( {5;0;0} \right)\) đến đường thẳng \(\Delta \) nhỏ nhất và bằng AH khi và chỉ khi K trùng H
Khi đó, đường thẳng \(\Delta \) được xác định là đường thẳng đi qua M và H.
Phương trình đường thẳng AH là \(\left\{ \begin{array}{l}x = 5 + t\\y = t\\z = t\end{array} \right. \Rightarrow \)Giả sử \(H\left( {5 + t;t;t} \right) \Rightarrow 5 + t + t + t - 2 = 0 \Leftrightarrow t = - 1 \Rightarrow H\left( {4; - 1; - 1} \right)\)
\( \Rightarrow \overrightarrow {MH} = \left( {4; - 1; - 3} \right) \Rightarrow \Delta \) có 1 VTCP là \(\overrightarrow {{u_3}} = \left( {4; - 1; - 3} \right)\).