Kết quả:
0/25
Thời gian làm bài: 00:00:00
Cho parabol \(\left( P \right)\) có đồ thị như hình vẽ:

Tính diện tích giới hạn bởi \(\left( P \right)\) và trục hoành.
Cho hình \(\left( H \right)\) giới hạn bởi đồ thị hàm số \(y = {x^3}\), trục hoành và hai đường thẳng \(x = 0,x = 1\). Thể tích khối tròn xoay tạo thành khi quay \(\left( H \right)\) quanh trục \(Ox\) được tính bởi:
Đổi biến $u = \ln x$ thì tích phân \(I = \int\limits_1^e {\dfrac{{1 - \ln x}}{{{x^2}}}dx} \) thành:
Đặt \(F\left( x \right) = \int\limits_1^x {\sin tdt} \). Khi đó \(F'\left( x \right)\) là hàm số nào dưới đây?
Hàm số \(F\left( x \right)\) được gọi là nguyên hàm của hàm số \(f\left( x \right)\) nếu:
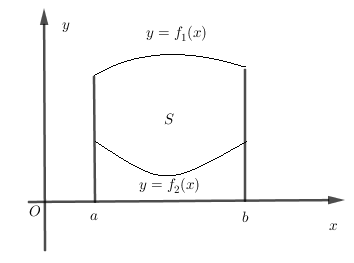
Cho hàm số \(y = {f_1}\left( x \right)\) và \(y = {f_2}\left( x \right)\) liên tục trên \(\left[ {a;b} \right]\) và có đồ thị như hình bên. Gọi \(S\) là hình phẳng giới hạn bới hai đồ thị trên và các đường thẳng \(x = a,x = b\). Mệnh đề nào sau đây đúng?
Tính \(I=\int\limits_{0}^{1}{{{e}^{3x}}dx}\).
Cho hàm số \(f\left( x \right)\) liên tục trên đoạn \(\left[ {a;b} \right]\). Chọn mệnh đề sai?
Nguyên hàm của hàm số \(f\left( x \right) = \sin x + \cos x\) là :
Biết \(F\left( x \right)\) là một nguyên hàm của hàm số \(f\left( x \right) = \sqrt {{{\ln }^2}x + 1} .\dfrac{{\ln x}}{x}\) thoả mãn \(F\left( 1 \right) = \dfrac{1}{3}\). Giá trị của \({F^2}\left( e \right)\) là
Cho tích phân \(I = \int\limits_0^{\dfrac{\pi }{2}} {\sin x\sqrt {8 + \cos x} dx} \). Đặt \(u = 8 + \cos x\) thì kết quả nào sau đây là đúng?
Diện tích hình phẳng được giới hạn bởi đồ thị hàm số \(y = x{e^x}\) , trục hoành, hai đường thẳng \(x = - 2;x = 3\) có công thức tính là
Nếu \(t = u\left( x \right)\) thì:
Họ nguyên hàm của hàm số \(y=\cos 3x\) là
Tìm nguyên hàm $F(x)$ của hàm số \(f(x)=6x+\sin 3x\), biết \(F(0)=\dfrac{2}{3}.\)
Tìm nguyên hàm của hàm số \(f(x) = \dfrac{x}{{\sqrt {3{x^2} + 2} }}\).
Tính nguyên hàm $I = \int {\dfrac{{\ln \left( {lnx} \right)}}{x}{\rm{d}}x} $ được kết quả nào sau đây?
Tính \(I = \int {x{{\tan }^2}xdx} \) ta được:
Tích phân $\int\limits_{ - 1}^5 {\left| {{x^2} - 2x - 3} \right|} dx$ có giá trị bằng:
Biết rằng \(\int\limits_0^1 {x\cos 2xdx} = \dfrac{1}{4}\left( {a\sin 2 + b\cos 2 + c} \right)\) với \(a,b,c \in Z\). Mệnh đề nào sau đây là đúng
Cho hai hàm số \(y = f(x)\) và \(y = g(x)\) liên tục trên đoạn \(\left[ {a;b} \right]\) với \(a < b\). Kí hiệu \({S_1}\) là diện tích hình phẳng giới hạn bởi các đường \(y = 3f(x)\), \(y = 3g(x),\,\,x = a,\,\,x = b,\,\,{S_2}\) là diện tích hình phẳng giới hạn bởi các đường \(y = f(x) - 2,\,\,y = g(x) - 2,\,\,x = a,\,\,x = b\). Khẳng định nào sau đây đúng?
Cho (H) là hình phẳng giới hạn bởi đồ thị hàm số \(y=\sqrt{x},\) trục hoành và đường thẳng \(x=9.\) Khi (H) quay quanh trục Ox tạo thành một khối tròn xoay có thể tích bằng:
Cho tích phân $I = \int\limits_0^{\dfrac{\pi }{4}} {\dfrac{{{x^2}}}{{{{\left( {x\sin x + \cos x} \right)}^2}}}{\rm{d}}x} = \dfrac{{m - \pi }}{{m + \pi }}$, giá trị của $m$ bằng :
Tìm họ nguyên hàm của hàm số $f(x) = {\tan ^5}x$.
Cho hàm số \(y = \frac{{x - {m^2}}}{{x + 1}}\) (với m là tham số khác 0) có đồ thị là \(\left( C \right)\). Gọi S là diện tích hình phẳng giới hạn bởi đồ thị \(\left( C \right)\) và hai trục tọa độ. Có bao nhiêu giá trị thực của m thỏa mãn \(S = 1\)?

