Đề kiểm tra học kì 2 - Đề số 4

Tích phân \(\int\limits_{1}^{3}{{{e}^{x}}dx}\) bằng:

Trong không gian với hệ tọa độ $Oxyz$, cho ba điểm

$A\left( {1;2; - 1} \right),{\rm{ }}B\left( {2;1;1} \right),{\rm{ }}C\left( {0;1;2} \right)$. Gọi $H\left( {a;b;c} \right)$ là trực tâm của tam giác \(ABC\). Giá trị của $a + b + c$ bằng:

Số phức $z$ thỏa mãn $\left| z \right| + z = 0$. Khi đó:

Trong các tích phân sau, tích phân nào có giá trị bằng \(2\)?

Khoảng cách giữa hai đường thẳng \({d_1}:\dfrac{x}{2} = \dfrac{{y - 1}}{{ - 1}} = \dfrac{z}{3},{d_2}:\dfrac{{x + 1}}{1} = \dfrac{y}{3} = \dfrac{{z + 1}}{{ - 2}}\) là:

Cho số phức $z = 1 + \sqrt {3}i $. Khi đó

Tìm nguyên hàm của hàm số \(f\left( x \right)=3\cos x+\dfrac{1}{{{x}^{2}}}\) trên \(\left( 0;\,+\infty \right)\).

Cho tam giác \(ABC\) có \(A\left( {0;0;1} \right)\), \(B\left( {0; - 1;0} \right)\) và \(C\left( {2;1; - 2} \right)\). Gọi \(G\) là trọng tâm tam giác. Phương trình đường thẳng \(AG\) là:

Viết phương trình mặt phẳng $\left( P \right)$  đi qua điểm $M\left( {1;0; - 2} \right)$ và vuông góc với hai mặt phẳng $\left( Q \right),\left( R \right)$  cho trước với $\left( Q \right):x + 2y - 3z + 1 = 0$  và $\left( {{\rm{ }}R} \right):2x - 3y + z + 1 = 0$ .

Tìm điểm $M$ biểu diễn số phức \(z = i - 2\)

 Với cách đổi biến \(u=\sqrt{1+3\ln x}\) thì tích phân \(\int\limits_{1}^{e}{\frac{\ln x}{x\sqrt{1+3\ln x}}}dx\) trở thành: 

Trong các khẳng định sau, khẳng định nào sai ?

Trong không gian $Oxyz$, cho mặt phẳng $(P):$ \(2x-y+3z-2=0\). Mặt phẳng (P) có một vecto pháp tuyến là

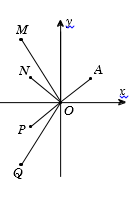
Cho số phức \(z\) thỏa mãn \(\left| z \right| = 1\) và điểm \(A\) trong hình vẽ bên là điểm biểu diễn của \(z\). Biết rằng trong hình vẽ bên, điểm biểu diễn của số phức $w = \dfrac{1}{{iz}}$ là một trong bốn điểm \(M,{\rm{ }}N,{\rm{ }}P,{\rm{ }}Q\). Khi đó điểm biểu diễn của số phức $w$ là

 Trong không gian với hệ tọa độ \(Oxyz,\) cho hai mặt phẳng \(\left( P \right):3x+y+z-5=0\) và \(\left( Q \right):x+2y+z-4=0.\) Khi đó, giao tuyến của \(\left( P \right)\) và \(\left( Q \right)\) có phương trình là 

Trong không gian với hệ tọa độ \(Oxyz\), mặt cầu tâm $I\left( {6,3, - 4} \right)$ tiếp xúc với $Ox$ có bán kính $R$ bằng:

Cho \({z_1},{z_2}\) là hai nghiệm của phương trình \({z^2} + 2iz + i = 0\). Chọn mệnh đề đúng:

Gọi $M$ và $N$ lần lượt là điểm biểu diễn của các số phức ${z_1};{z_2}$ khác $0$. Khi đó khẳng định nào sau đây sai ?

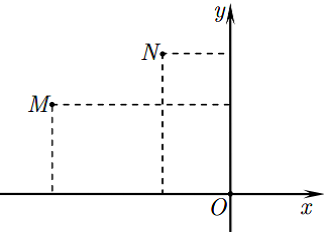
Trong không gian $Oxyz$, điểm nào dưới đây nằm trên mặt phẳng $(P): 2x – y + z – 2 = 0$?

Chọn kết luận đúng:

Trong không gian \(Oxyz,\) cho mặt cầu \((S):{{(x-1)}^{2}}+{{(y-2)}^{2}}+{{(z+1)}^{2}}=6,\) tiếp xúc với hai mặt phẳng \((P):x+y+2z\,+\,5=0,\,\,(Q):2x-y+z\,-\,5=0\) lần lượt tại các tiếp điểm \(A,\,\,B.\) Độ dài đoạn thẳng \(AB\) là

Đổi biến $u = \ln x$ thì tích phân \(I = \int\limits_1^e {\dfrac{{1 - \ln x}}{{{x^2}}}dx} \) thành:

Giả sử \(A,B\) là các hằng số của hàm số \(f\left( x \right) = A\sin \pi x + B{x^2}\). Biết \(\int\limits_0^2 {f\left( x \right)dx}  = 4\), giá trị của \(B\) là:

Trong không gian với hệ tọa độ \(Oxyz,\) cho điểm \(A\left( {1;0;2} \right)\) và đường thẳng \(d:\dfrac{{x - 1}}{1} = \dfrac{y}{1} = \dfrac{{z + 1}}{2}\). Viết phương trình đường thẳng \(\Delta \) đi qua \(A,\) vuông góc và cắt \(d\).

Trong không gian với hệ tọa độ $Oxyz$ cho mặt phẳng $(\alpha ):4x + 3y - 7z + 3 = 0$ và điểm $I(0;1;1)$. Phương trình mặt phẳng $(\beta )$ đối xứng với $(\alpha )$ qua $I$ là:

Trong không gian với hệ tọa độ \(Oxyz,\) phương trình nào dưới đây là phương trình mặt cầu tâm \(I\left( 1;0;-\,2 \right),\) bán kính \(R=4\,\,?\)

Cho số phức $z = 2 + 3i$. Tìm số phức \(w = \left( {3 + 2i} \right)z + 2\overline z \)

Trong không gian với hệ tọa độ \(Oxyz,\) tam giác \(ABC\) có \(A\left( -\,1;-\,2;4 \right),\,\,B\left( -\,4;-\,2;0 \right)\) và \(C\left( 3;-\,2;1 \right).\) Tính số đo của góc \(B.\)

Trong không gian với hệ tọa độ \(Oxyz\), cho mặt cầu \(\left( S \right):{x^2} + {y^2} + {z^2} - 6x - 4y - 2z = 0\). Điểm nào sau đây thuộc mặt cầu \(\left( S \right)\)?

Tính tổng \(T\) của phần thực và phần ảo của số phức \(z = {\left( {\sqrt 2  + 3i} \right)^2}.\)

Biết \(F\left( x \right)\) là một nguyên hàm của hàm số \(f\left( x \right)={{x}^{2}}+2x-3\) thỏa mãn \(F\left( 0 \right)=4,\) giá trị của \(F\left( 1 \right)\) bằng

Tính tích phân \(I = \int\limits_0^{\dfrac{\pi }{2}} {{{\left( {1 - \cos x} \right)}^n}\sin xdx} \) bằng:

Cho $F\left( x \right) = {x^2}$ là nguyên hàm của hàm số $f\left( x \right){e^{2x}}$ và $f\left( x \right)$ là hàm số thỏa mãn điều kiện $f\left( 0 \right) =  0,\,\,f\left( 1 \right) = \dfrac{2}{e^2}.$ Tính tích phân $I = \int\limits_0^1 {f'\left( x \right){e^{2x}}{\rm{d}}x} .$

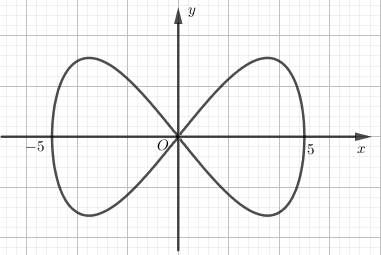
Trong Công viên Toán học có những mảnh đất hình dáng khác nhau. Mỗi mảnh được trồng một loài hoa và nó được tạo thành bởi một trong những đường cong đẹp nhất trong toán học. Ở đó có mảnh đất mang tên Bernoulli, nó được tạo thành từ đường Lemniscate có phương trình trong hệ tọa độ $Oxy$ là \(16{y^2} = {x^2}\left( {25 - {x^2}} \right)\) như hình vẽ bên. Tính diện tích $S$ của mảnh đất Bernoulli biết rằng mỗi đơn vị trong hệ trục tọa độ $Oxy$ tương ứng với chiều dài $1$ mét

Vòm cửa lớn của một trung tâm văn hóa có hình parabol. Gắn parabol vào hệ trục \(Oxy\) thì nó có đỉnh \(\left( {0;8} \right)\) và cắt trục hoành tại 2 điểm phân biệt, trong đó có 1 điểm là \(\left( { - 4;0} \right)\). Người ta dự định lắp vào cửa kính cho vòm cửa này. Hãy tính diện tích mặt kính cần lắp vào.

Thể tích khối tròn xoay do hình phẳng giới hạn bởi các đồ thị $y =  - \,\sqrt {4 - {x^2}} ,\,\,{x^2} + 3y = 0$ quay quanh trục $Ox$ là $V = \dfrac{{a\pi \sqrt 3 }}{b},$ với $a,\,\,b > 0$ và $\dfrac{a}{b}$ là phân số tối giản. Tính tổng $T = a + b.$

Cho hình phẳng $\left( H \right)$ giới hạn bởi \(y = \dfrac{1}{3}{x^3} - {x^2}\) và $Ox$.  Thể tích khối tròn xoay sinh ra khi quay $\left( H \right)$  quanh $Ox$ bằng :

Tính môđun của số phức $z$ biết $\overline z  = \left( {4 - 3i} \right)\left( {1 + i} \right)$.

Gọi \({z_1};{z_2};{z_3};{z_4}\) là bốn nghiệm phức của phương trình \(2{z^4} - 3{z^2} - 2 = 0\). Tổng \(T = |{z_1}{|^2} + |{z_2}{|^2} + |{z_3}{|^2} + |{z_4}{|^2}\) bằng:

Hỏi có bao nhiêu số phức thỏa mãn đồng thời các điều kiện $\left| {z - i} \right| = 5$ và \({z^2}\) là số thuần ảo?

Cho ba điểm $A,B,C$ lần lượt biểu diễn các số phức sau \({z_1} = 1 + i;\,{z_2} = {z_1}^2;\,{z_3} = m - i\). Tìm các giá trị thực của $m$ sao cho tam giác $ABC$ vuông tại $B$.

Trong số các số phức $z$ thỏa mãn điều kiện \(\left| {z - 4 + 3i} \right| = 3\), gọi ${z_0}$ là số phức có mô đun lớn nhất. Khi đó \(\left| {{z_0}} \right|\) là

Trong không gian với hệ tọa độ \(Oxyz,\) cho điểm \(M\left( 1;2;3 \right).\) Mặt phẳng \(\left( P \right)\) đi qua M và cắt các tia \(Ox;\,\,Oy;\,\,Oz\) lần lượt tại các điểm \(A;\,\,B;\,\,C\) \(\left( A;\,\,B;\,\,C\ne O \right)\) sao cho thể tích của tứ diện \(OABC\) nhỏ nhất. Phương trình của mặt phẳng \(\left( P \right)\) là

Trong không gian với hệ tọa độ \(Oxyz\), cho đường thẳng \(\Delta :\left\{ {\begin{array}{*{20}{c}}{x = t{\rm{      }}}\\{y = 8 + 4t}\\{z = 3 + 2t}\end{array}} \right.\) và mặt phẳng $\left( P \right):x + y + z - 7 = 0.$ Phương trình đường thẳng \(\Delta '\) là hình chiếu vuông góc của \(\Delta \) trên \(\left( P \right)\) là:

Trong không gian với hệ tọa độ $Oxyz$, phương trình mặt phẳng \((P)\) đi qua hai điểm \(A(1;1;2),B(0; - 1;1)\)  và song song với đường thẳng $d:\dfrac{{x - 1}}{1} = \dfrac{{y + 1}}{{ - 1}} = \dfrac{z}{2}$ là:

Trong không gian với hệ tọa độ ${\rm{Ox}}yz$. Hãy viết phương trình  mặt cầu $(S)$ có tâm \(I(2\,;\,0;1)\) và tiếp xúc với đường thẳng \(d: \dfrac{{x - 1}}{1} = \dfrac{y}{2} = \dfrac{{z - 2}}{1}\).

Trong không gian với hệ tọa độ \(Oxyz\), cho đường thẳng \(d:\dfrac{{x - 3}}{1} = \dfrac{{y - 3}}{3} = \dfrac{z}{2}\), mặt phẳng \(\left( \alpha  \right):x + y - z + 3 = 0\) và điểm \(A\left( {1;2 - 1} \right)\). Đường thẳng \(\Delta \) đi qua \(A\) cắt \(d\) và song song với mặt phẳng \(\left( \alpha  \right)\) có phương trình là:

Trong không gian \(Oxyz\), cho mặt cầu \(\left( S \right):{{x}^{2}}+{{y}^{2}}+{{z}^{2}}-2x-2y+4z-1=0\) và mặt phẳng \(\left( P \right):x+y-z-m=0.\) Tìm tất cả m để \(\left( P \right)\) cắt \(\left( S \right)\) theo giao tuyến là một đường tròn có bán kính lớn nhất.

Cho số phức $z$ thỏa mãn $\left| {z - 2} \right| = 2$. Biết rằng tập hợp các điểm biểu diễn các số phức $w = \left( {1 - i} \right)z + i$ là một đường tròn. Tính bán kính $r$ của đường tròn đó

Cho hàm số $f(x)$ liên tục, \(f(x)>-1,\,f(0)=0\) và thỏa mãn \(f'(x)\sqrt{{{x}^{2}}+1}=2x\sqrt{f(x)+1}\). Tính \(f\left( \sqrt{3} \right)\).