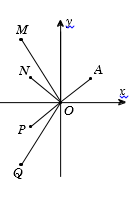
Cho số phức \(z\) thỏa mãn \(\left| z \right| = 1\) và điểm \(A\) trong hình vẽ bên là điểm biểu diễn của \(z\). Biết rằng trong hình vẽ bên, điểm biểu diễn của số phức $w = \dfrac{1}{{iz}}$ là một trong bốn điểm \(M,{\rm{ }}N,{\rm{ }}P,{\rm{ }}Q\). Khi đó điểm biểu diễn của số phức $w$ là

Gọi \(z = x + yi{\rm{ }}\left( {x;{\rm{ }}y \in \mathbb{R}} \right).\) Từ giả thiết, ta có \(\left\{ \begin{array}{l}{x^2} + {y^2} = 1\\x > 0;{\rm{ }}y > 0\end{array} \right..\)

Ta có $w = \dfrac{1}{{iz}} =  - \dfrac{i}{z} =  - \dfrac{i}{{x + yi}} =  - \dfrac{{i\left( {x - yi} \right)}}{{\left( {x + yi} \right)\left( {x - yi} \right)}} =  - \dfrac{{y + xi}}{{{x^2} + {y^2}}} =  - \,y - xi.$

Vì $x > 0,{\rm{ }}y > 0$ nên điểm biểu diễn số phức $w$ có tọa độ là $\left( { - \,y; - \,x} \right)$ (đều có hoành độ và tung độ âm). Đồng thời $\left| w \right| = \sqrt {{{\left( { - y} \right)}^2} + {{\left( { - x} \right)}^2}}  = 1 = \left| z \right|.$ Suy ra điểm biểu diễn của số phức $w$ nằm trong góc phần tư thứ III và cách gốc tọa độ \(O\) một khoảng bằng \(OA.\) Quan sát hình vẽ ta thấy có điểm \(P\) thỏa mãn.