Kết quả:
0/25
Thời gian làm bài: 00:00:00
Số mặt phẳng đối xứng của hình hộp chữ nhật (các kích thước khác nhau) là:
Khối đa diện đều có $20$ mặt thì có bao nhiêu cạnh?
Cho khối chóp \(S.ABC\). Trên các cạnh \(SA,SB,SC\) lấy các điểm \(A',B',C'\) sao cho \(A'A = 2SA',B'B = 2SB',C'C = 2SC'\), khi đó tồn tại một phép vị tự biến khối chóp \(S.ABC\) thành khối chóp \(S.A'B'C'\) với tỉ số đồng dạng là:
Hình tứ diện đều có mấy mặt phẳng đối xứng?
Trong các khẳng định sau, khẳng định nào sai?
Cho khối chóp tam giác \(S.ABC\), trên các cạnh \(SA,SB,SC\) lần lượt lấy các điểm \(A',B',C'\). Khi đó:
Cho hình lăng trụ đứng \(ABCD.A'B'C'D'\) có đáy là tứ giác đều cạnh $a$, biết rằng \(BD' = a\sqrt 6 \) . Tính thể tích của khối lăng trụ?
Phép dời hình biến đoạn thẳng thành:
Cho hai hình chóp tam giác đều cạnh đáy bằng \(a\). Cần bổ sung thêm điều kiện gì để hai hình chóp đó bằng nhau?
Trong các kí hiệu sau, kí hiệu nào không phải của khối đa diện đều?
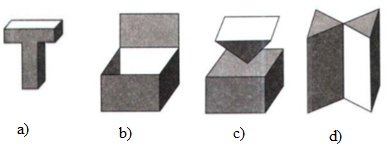
Trong các hình dưới đây, hình nào là khối đa diện?
Khối đa diện đều loại \(\left\{ {n;p} \right\}\) thì \(n\) là:
Vật thể nào trong các vật thể sau không phải là khối đa diện?
Trong các mệnh đề sau mệnh đề nào đúng:
Cho khối lăng trụ tam giác đều \(ABC.{A_1}{B_1}{C_1}\) có tất cả các cạnh bằng \(a\). Gọi \(M\) là trung điểm của \(A{A_1}\). Thể tích khối chóp \(M.BC{A_1}\) là:
Cho hình chóp \(S.ABC\) đáy \(ABC\) là tam giác vuông tại \(A,AB = a,AC = a\sqrt 3 \). Tam giác $SBC$ đều nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp $S.ABC$
Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \(a\). Mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SAD} \right)\) cùng vuông góc với mặt phẳng \(\left( {ABCD} \right)\). Đường thẳng \(SC\) tạo với đáy góc \({45^0}\). Gọi \(M,N\) lần lượt là trung điểm của \(AB\) và \(AD\). Thể tích của khối chóp \(S.MCDN\) là:
Cho tứ diện \(ABCD\) có các cạnh \(AB,AC,AD\) đôi một vuông góc với nhau, \(AB = 6a,AC = 7a,AD = 4a\). Gọi \(M,N,P\) lần lượt là trung điểm của các cạnh \(BC,CD,DB\). Thể tích \(V\) của tứ diện \(AMNP\) là:
Cho hình lăng trụ $ABC.A’B’C’$ có độ dài tất cả các cạnh bằng $a$ và hình chiếu vuông góc của đỉnh $C$ trên $(ABB’A’)$ là tâm của hình bình hành $ABB’A’$. Thể tích của khối lăng trụ là:
Cho lăng trụ đứng \(ABC.A'B'C'\) với $ABC$ là tam giác vuông cân tại $C$ có \(AB = a\) , mặt bên \(ABB'A'\) là hình vuông. Mặt phẳng qua trung điểm $I$ của $AB$ và vuông góc với \(AB'\) chia khối lăng trụ thành 2 phần. Tính thể tích mỗi phần?
Cho hình lăng trụ xiên $ABC.A’B’C’$ có đáy $ABC$ là tam giác đều với tâm $O$. Hình chiếu của $C’$ trên $(ABC) $ là $O$. Tính thể tích của lăng trụ biết rằng khoảng cách từ $O$ đến $CC’$ là $a$ và 2 mặt bên $(ACC’A’)$ và $(BCC’B’)$ hợp với nhau góc \({90^0}\).
Cho hình lăng trụ $ABC.A'B'C'$ có đáy $ABC$ là tam giác cân \(AB = AC = a;\widehat {BAC} = {120^0}\) và $AB'$ vuông góc với $\left( {A'B'C'} \right)$ . Mặt phẳng $\left( {AA'C'} \right)$ tạo với mặt phẳng $\left( {A'B'C'} \right)$ một góc \({30^0}\). Thể tích khối lăng trụ $ABC.A'B'C'$ là:
Cho hình chóp đều $S.ABCD$ có cạnh đáy bằng $2a$. Khoảng cách giữa hai đường thẳng $SA$ và $CD$ bằng \(a\sqrt 3 \). Thể tích khối chóp $S.ABCD$ là:
Cho khối đa diện mà mỗi đỉnh là đỉnh chung của \(3\) cạnh. Kí hiệu \(D\) là số đỉnh, \(C\) là số cạnh. Chọn mệnh đề đúng:
Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \(a\), \(SA\) vuông góc với mặt phẳng đáy \(\left( {ABCD} \right)\) và \(SA = a\). Điểm $M$ thuộc cạnh $SA$ sao cho \(\dfrac{{SM}}{{SA}} = k\). Xác định $k$ sao cho mặt phẳng \(\left( {BMC} \right)\) chia khối chóp \(S.ABCD\) thành hai phần có thể tích bằng nhau.
