Đề thi thử THPTQG - Đề số 3

Cho \(y = f\left( x \right)\) là hàm số lẻ và liên tục trên \(\left[ { - a;a} \right]\). Chọn kết luận đúng:

Cho đường thẳng \(d:\left\{ \begin{array}{l}x =  - t\\y = 1 - t\\z = t\end{array} \right.\left( {t \in \mathbb{R}} \right)\). Điểm nào trong các điểm dưới đây thuộc đường thẳng \(d\)?

Tìm phương trình chính tắc của Elip có tâm sai bằng $\dfrac{1}{3}$ và trục lớn bằng \(6\).

Cho số phức \(z = \dfrac{{7 - 11i}}{{2 - i}}\) . Tìm phần thực và phần ảo của \(\overline z \) .

Nghiệm của phương trình \(\sqrt 3 \tan x + 3 = 0\) là:

Tính thể tích \(V\) của khối trụ ngoại tiếp hình lập phương có cạnh bằng $a$.

Trong không gian với hệ tọa độ  $Oxyz$, cho hai điểm  \(A(1;4;2)\) , \(B( - 1;2;4)\). Tìm tọa độ điểm $M$ thuộc trục $Oz$  sao cho :\(M{A^2} + M{B^2} = 32\).

Đáy của hình lăng trụ đứng tam giác \(ABC.A'B'C'\) là tam giác đều cạnh \(a = 4\) và biết diện tích tam giác \(A'BC\) bằng $8$ . Tính thể tích khối lăng trụ?

Cho hàm số \(y = \dfrac{{{x^2}}}{4} - x + 1\) có đồ thị \(\left( C \right)\). Từ điểm \(M\left( {2; - 1} \right)\) có thể kẻ đến \(\left( C \right)\) hai tiếp tuyến phân biệt, hai tiếp tuyến này có phương trình là?

Trong các dãy số sau, dãy số nào là cấp số cộng?

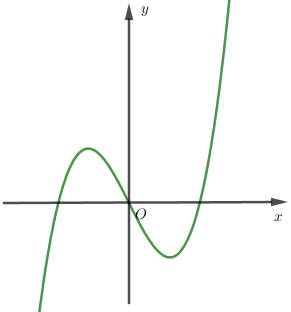
Hàm số nào sau đây có thể có đồ thị dạng như hình vẽ?

Trong không gian với hệ tọa độ Oxyz cho mặt cầu có phương trình: \({x^2} + {y^2} + {z^2} - 2x + 4y - 6z + 9 = 0\). Mặt cầu có tâm I và bán kính R là:

Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên như sau:

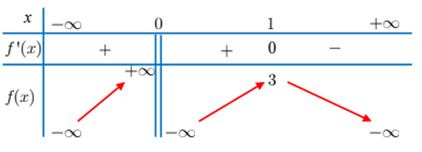
Với các giá trị thực của tham số \(m\), phương trình \(f\left( x \right)=m\) có nhiều nhất bao nhiêu nghiệm?

Giá trị nhỏ nhất của hàm số $y = 2x + \cos x$ trên đoạn $\left[ {0;1} \right]$ là :

Tìm số hạng không chứa $x$ trong khai triển ${\left( {x{y^2} - \dfrac{1}{{xy}}} \right)^8}.$

Chọn mệnh đề đúng:

Viết các số sau theo thứ tự tăng dần: $a = {1^{3,8}};\,\,b = {2^{ - 1}};\,\,c = {\left( {\dfrac{1}{2}} \right)^{ - 3}}$

Trong mặt phẳng tọa độ với hệ tọa độ $Oxy$ , cho các điểm \(A(4;0),B(1;4),C(1; - 1)\) . Gọi $G$ là trọng tâm của tam giác $ABC$ . Biết rằng $G$ là điểm biểu diễn số phức $z$ . Mệnh đề nào sau đây là đúng?

Trong không gian với hệ trục $Oxyz$, cho đường thẳng \(d\) đi qua điểm $M\left( {2,0, - 1} \right)$ và có vecto chỉ phương \(\vec a = (4, - 6,2)\). Phương trình tham số của đường thẳng d là:

Gọi $F(x)$ là một nguyên hàm của hàm số \(y = x.\cos x\) mà $F(0) = 1$. Phát biểu nào sau đây đúng:

Cho hai số thực dương \(a\) và \(b\) thỏa mãn \({\log _4}a = {\log _6}b = {\log _9}(a + b).\)Tính tỉ số \(\dfrac{a}{b}\).

Tìm $m$ để hàm số $y = \dfrac{{{x^3}}}{3} - 2m{x^2} + 4mx + 2$ nghịch biến trên khoảng $\left( { - 2;0} \right)$.

Cho hàm số \(y = {x^3} - 3{x^2} - 9x + m\). Viết phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số.

Gọi giá trị lớn nhất và nhỏ nhất của hàm số $y = {x^4} + 2{x^2} - 1$ trên đoạn $\left[ { - 1;2} \right]$ lần lượt là $M$ và $m$. Khi đó giá trị của $M.m$ là:

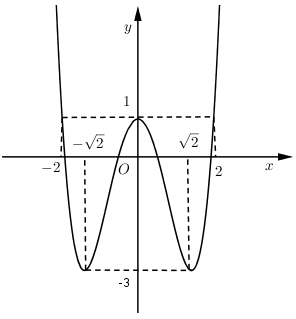
Đồ thị hàm số bên là đồ thị của hàm số $y = {x^4} - 4{x^2} + 1\left( C \right).$ Tìm $m$ để phương trình ${x^4} - 4{x^2} + 1 - m = 0$ có $4$ nghiệm phân biệt 

Gọi \(M\left( a;b \right)\) là điểm trên đồ thị hàm số \(y=\dfrac{2x+1}{x+2}\) mà có khoảng cách đến đường thẳng \(d:y=3x+6\) nhỏ nhất. Khi đó

Tìm tập hợp tất cả các giá trị thực của m để đồ thị \(\left( {{C}_{m}} \right)\) của hàm số \(y={{x}^{4}}-m{{x}^{2}}+2m-3\) có 4 giao điểm với đường thẳng \(y=1\), có hoành độ nhỏ hơn 3.

Đặt $a = \log_{2}3, b = \log_{5}3$. Hãy biểu diễn $\log_{6}45$ theo $a$ và $b$:

Cho phương trình \({\log _3}x.{\log _5}x = {\log _3}x + {\log _5}x\) . Khẳng định nào sau đây là đúng?

Cho hình chóp đều $S.ABCD$ có cạnh đáy bằng $2a$. Khoảng cách giữa hai đường thẳng $SA$ và $CD$ bằng \(a\sqrt 3 \). Thể tích khối chóp $S.ABCD$ là:

Cho hàm số $f\left( x \right) = {5^x}{.9^{{x^3}}}$, chọn phép biến đổi sai khi giải bất phương trình:

Tính tích phân $I = \int\limits_0^3 {\dfrac{{{\rm{d}}x}}{{x + 2}}} $. 

Bất phương trình $\sqrt {2{x^3} + 3{x^2} + 6x + 16}  - \sqrt {4 - x}  \geqslant 2\sqrt 3 $ có tập nghiệm là $\left[ {a;b} \right].$ Hỏi tổng $a + b$ có giá trị là bao nhiêu?

Tích phân \(I = \int\limits_{\frac{\pi }{3}}^{\frac{\pi }{2}} {\dfrac{{dx}}{{\sin x}}} \) có giá trị bằng

Cho \({z_1}\), \({z_2}\) là hai số phức thỏa mãn \({z^2} - 4z + 5 = 0\). Tính giá trị biểu thức \(P = {\left( {{z_1} - 1} \right)^{2017}} + {\left( {{z_2} - 1} \right)^{2017}}\).

Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \(a\). Mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SAD} \right)\) cùng vuông góc với mặt phẳng \(\left( {ABCD} \right)\). Đường thẳng \(SC\) tạo với đáy góc \({45^0}\). Gọi \(M,N\) lần lượt là trung điểm của \(AB\) và \(AD\). Thể tích của khối chóp \(S.MCDN\) là:

Cho hai mặt phẳng $\left( P \right)$ và $\left( Q \right)$ lần lượt có phương trình $x + 2y - 2z + 1 = 0$ và $x - 2y + 2z - 1 = 0$. Gọi $\left( S \right)$ là quỹ tích các điểm cách đều hai mặt phẳng $\left( P \right)$ và $\left( Q \right)$.  Tìm khẳng định đúng.

Cho hình chóp tam giác đều $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a$, cạnh \(SA = \dfrac{{2a\sqrt 3 }}{3}\) . Gọi $D$ là điểm đối xứng của $B$ qua $C$. Tính bán kính $R$ của mặt cầu ngoại tiếp hình chóp $S.ABD$ 

Cho tam giác $ABC$ biết $A\left( {2;4; - 3} \right)$ và trọng tâm $G$ của tam giác có toạ độ là $G\left( {2;1;0} \right)$. Khi đó \(\overrightarrow {AB}  + \overrightarrow {AC} \) có tọa độ là

Cho parabol $\left( P \right):y = {x^2} + 1$  và đường thẳng $\left( d \right):y = mx + 2$. Biết rằng tồn tại $m$ để diện tích hình phẳng giới hạn bới $\left( P \right)$  và $\left( d \right)$  đạt giá trị nhỏ nhất, tính diện tích nhỏ nhất đó.

Cho hai điểm \(M\left( {1; - 2; - 4} \right),M'\left( {5; - 4;2} \right)\). Biết \(M'\) là hình chiếu của \(M\) lên mặt phẳng \(\left( P \right)\). Khi đó, phương trình \(\left( P \right)\) là:

Cho hàm số \(f\left( x \right)\) xác định trên $[a; b].$ Trong các khẳng định sau, khẳng định nào đúng?

Trong mặt phẳng với hệ tọa độ $Oxy$, cho đường thẳng $\Delta $ có phương trình $5x - y + 1 = 0$. Thực hiện phép tịnh tiến theo phương của trục hoành về phía trái $2$ đơn vị, sau đó tiếp tục thực hiện phép tịnh tiến theo phương của trục tung về phía trên $3$ đơn vị, đường thẳng $\Delta $ biến thành đường thẳng $\Delta '$ có phương trình là:

Cho tứ diện đều $ABCD$  cạnh $a$ . Gọi $M$  và $P$  lần lượt là hai điểm di động trên các cạnh $AD$  và $BC$  sao cho $MA = PC = x\left( {0 < x < \dfrac{a}{2}} \right)$ . Mặt phẳng \(\left( \alpha  \right)\) đi qua $MP$  song song với $CD$  cắt tứ diện theo một thiết diện là hình gì?

Cho hình lăng trụ đều \(ABC.A'B'C'\) có tất cả các cạnh bằng a. Gọi M là trung điểm của cạnh BC. Khoảng cách giữa hai đường thẳng AM và B’C là :

Tìm $m \ne 0$ để phương trình ${x^2}\left| {x - 3} \right| = m + \dfrac{1}{m}$ có 4 nghiệm phân biệt.

Cho \(a > b > 0\) và \(x = \dfrac{{1 + a}}{{1 + a + {a^2}}}\), \(y = \dfrac{{1 + b}}{{1 + b + {b^2}}}\). Mệnh đề nào sau đây đúng?

Một con xúc sắc cân đối, đồng chất được gieo \(6\) lần. Xác suất để được một số lớn hơn hay bằng \(5\) xuất hiện ít nhất \(5\) lần là:

Gọi $m$ là số chữ số cần dùng khi viết số $2^{30}$ trong hệ thập phân và $n$ là số chữ số cần dùng khi viết số $30^2$ trong hệ nhị phân. Ta có tổng $m + n$ bằng

Trong không gian với hệ tọa độ \(Oxyz\), cho đường thẳng \(d:\left\{ \begin{array}{l}x =  - \dfrac{9}{5} - t\\y = 5t\\z = \dfrac{7}{5} + 3t\end{array} \right.\) và mặt phẳng \(\left( P \right):3x - 2y + 3z - 1 = 0\).

Gọi \(d'\) là hình chiếu của \(d\) trên mặt phẳng \(\left( P \right)\). Trong các vectơ sau, vectơ nào không phải là vectơ chỉ phương của \(d'\)?