Kết quả:
0/25
Thời gian làm bài: 00:00:00
Họ nguyên hàm của hàm số \(f\left( x \right)=2x+\sin 2x\) là:
Nếu \(f\left( 1 \right) = 12,f'\left( x \right)\) liên tục và \(\int\limits_1^4 {f'\left( x \right)dx} = 17\) thì giá trị của \(f\left( 4 \right)\) bằng:
Chọn mệnh đề đúng:
Cho hàm số $f\left( x \right)$ liên tục trên $R$ và $\int\limits_{ - 2}^4 {f\left( x \right)} dx{\rm{ = 2}}$ . Mệnh đề nào sau đây là sai?
Hàm số nào không là nguyên hàm của hàm số \(y = 3{x^4}\)?
Biết \(F\left( x \right)\) là một nguyên hàm của hàm số\(f\left( x \right) = \dfrac{x}{{\sqrt {8 - {x^2}} }}\) thoả mãn \(F\left( 2 \right) = 0\). Khi đó phương trình \(F\left( x \right) = x\) có nghiệm là
Cho hàm số \(y = f\left( x \right)\) là hàm số chẵn trên \(\mathbb{R}\) và \(a\) là một số thực dương. Chọn kết luận đúng:
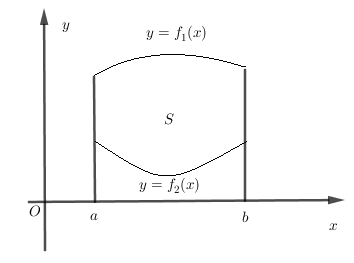
Cho hai hàm số \(y = {f_1}\left( x \right)\) và \(y = {f_2}\left( x \right)\) liên tục trên đoạn \(\left[ {a;b} \right]\) và có đồ thị như hình vẽ bên. Gọi $S$ là hình phẳng giới hạn bởi hai đồ thị trên và các đường thẳng \(x = a,x = b\). Thể tích $V$ của vật thể tròn xoay tạo thành khi quay $S$ quanh trục $Ox$ được tính bởi công thức nào sau đây ?
Cho hai hàm số \(f,\,\,g\) liên tục trên đoạn $\left[ {a;b} \right]$ và số thực $k$ tùy ý. Trong các khẳng định sau, khẳng định nào sai ?
Diện tích hình phẳng giới hạn bởi các đồ thị hàm số $y = {x^3} - x;y = 2x$ và các đường thẳng $x = - 1;x = 1$ được xác định bởi công thức:
Tích phân \(I = \int\limits_1^2 {{x^5}} dx\) có giá trị là:
Công thức tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right) = {x^2} - 1\), trục hoành và hai đường thẳng \(x = - 1;x = - 3\) là:
Nếu \(t = u\left( x \right)\) thì:
Biết $\int {f\left( x \right){\mkern 1mu} {\rm{d}}x = 2x\ln \left( {3x - 1} \right) + C} $ với $x \in \left( {\dfrac{1}{9}; + \infty } \right)$. Tìm khẳng định đúng trong các khẳng định sau.
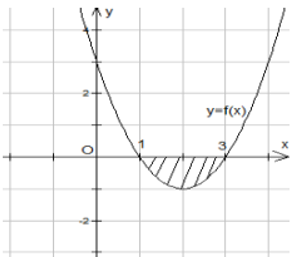
Cho hàm số \(y=f\left( x \right)\) liên tục và có đồ thị như hình bên. Gọi \(D\) là hình phẳng giới hạn bởi đồ thị hàm số đã cho và trục \(Ox.\) Quay hình phẳng \(D\) quanh trục \(Ox\) ta được khối tròn xoay có thể tích \(V\) được xác định theo công thức
Cho hàm số \(f\left( x \right) = {e^{ - 2018x + 2017}}\). Gọi \(F\left( x \right)\) là một nguyên hàm của \(f\left( x \right)\) mà \(F\left( 1 \right) = e\). Chọn mệnh đề đúng:
Cho nguyên hàm \(\int {x\sin xdx} \). Nếu đặt \(\left\{ \begin{array}{l}u = x\\dv = \sin xdx\end{array} \right.\) thì:
Cho \(F(x) = - \dfrac{1}{{3{x^3}}}\) là một nguyên hàm của hàm số \(\dfrac{{f(x)}}{x}\). Tìm nguyên hàm của hàm số \(f'(x)\ln x\).
Nếu \(\int\limits_{ - 2}^0 {\left( {4 - {e^{ -{\frac{x}{2}}}}} \right)dx} = K - 2e\) thì giá trị của \(K\) là
Kết quả tích phân \(I = \int\limits_1^e {\dfrac{{\ln x}}{{x\left( {{{\ln }^2}x + 1} \right)}}dx} \) có dạng \(I = a\ln 2 + b\) với \(a,b \in Q\) . Khẳng định nào sau đây là đúng?
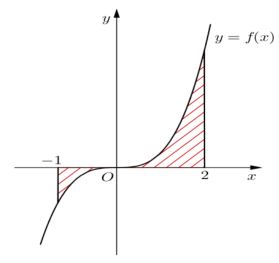
Gọi \(S\) là diện tích hình phẳng \(\left( H \right)\) giới hạn bởi các đường $y=f\left( x \right),~$trục hoành và hai đường thẳng \(x = - 1,x = 2\) (như hình vẽ). Đặt $a=\underset{-1}{\overset{0}{\mathop \int }}\,f\left( x \right)dx,~b=\underset{0}{\overset{2}{\mathop \int }}\,f\left( x \right)dx.$ Mệnh đề nào sau đây đúng?
Thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường \(y=x{{e}^{x}},\ \ y=0,\ x=0,\ x=1\) xung quanh trục \(Ox\) là:
Biết \(\int\limits_{0}^{1}{\frac{\pi {{x}^{3}}+{{2}^{x}}+\text{e}{{x}^{3}}{{.2}^{x}}}{\pi +\text{e}{{.2}^{x}}}\text{d}x}=\frac{1}{m}+\frac{1}{\text{e}\ln n}\ln \left( p+\frac{\text{e}}{\text{e}+\pi } \right)\) với \(m\), \(n\), \(p\) là các số nguyên dương. Tính tổng \(S=m+n+p\).
Tìm thể tích \(V\) của vật tròn xoay sinh ra bởi đường tròn \({{x}^{2}}+{{\left( y-3 \right)}^{2}}=4\) khi quay quanh trục \(Ox.\)
Cho tích phân $I = \int\limits_0^{\dfrac{\pi }{4}} {\dfrac{{{x^2}}}{{{{\left( {x\sin x + \cos x} \right)}^2}}}{\rm{d}}x} = \dfrac{{m - \pi }}{{m + \pi }}$, giá trị của $m$ bằng :
