Tìm thể tích \(V\) của vật tròn xoay sinh ra bởi đường tròn \({{x}^{2}}+{{\left( y-3 \right)}^{2}}=4\) khi quay quanh trục \(Ox.\)
Trả lời bởi giáo viên
Ta có \({{x}^{2}}+{{\left( y-3 \right)}^{2}}=4\Leftrightarrow {{\left( y-3 \right)}^{2}}=4-{{x}^{2}}\Leftrightarrow \left[\begin{align} & y=f\left( x \right)=\sqrt{4-{{x}^{2}}}+3 \\ & y=g\left( x \right)=-\,\sqrt{4-{{x}^{2}}}+3 \\\end{align} \right.\)
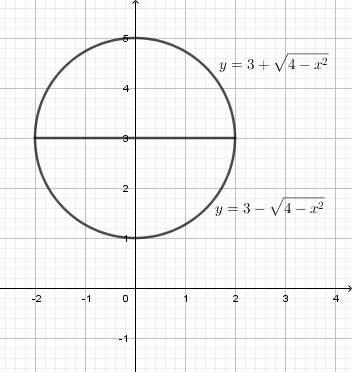
Vậy thể tích khối tròn xoay cần tính là \(V=\pi \int\limits_{-\,2}^{2}{{{f}^{2}}\left( x \right)\,\text{d}x}-\pi \int\limits_{-\,2}^{2}{{{g}^{2}}\left( x \right)\,\text{d}x}\)
\(\begin{align} & =\pi \int\limits_{-\,2}^{2}{\left( {{f}^{2}}\left( x \right)-{{g}^{2}}\left( x \right) \right)\,\text{d}x} \\ & =\pi \int\limits_{-\,2}^{2}{\left( {{\left( \sqrt{4-{{x}^{2}}}+3 \right)}^{2}}-{{\left( 3-\sqrt{4-{{x}^{2}}} \right)}^{2}} \right)\,\text{d}x} \\ & =\pi \,\int\limits_{-\,2}^{2}{12\sqrt{4-{{x}^{2}}}\,\text{d}x}=24{{\pi }^{2}}. \\\end{align}\)
Vậy thể tích cần tính là \(V=24{{\pi }^{2}}.\)
Hướng dẫn giải:
Sử dụng công thức tính thể tích khối tròn xoay được quay quanh trục hoành của các đồ thị hàm số : \(y=f\left( x \right);\ x=a;\ x=b\ \ \left( a<b \right)\) là : \(V=\pi \int\limits_{a}^{b}{{{f}^{2}}\left( x \right)}dx.\)

