Đề thi thử THPTQG - Đề số 5

Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như sau. Khẳng định nào dưới đây là đúng?

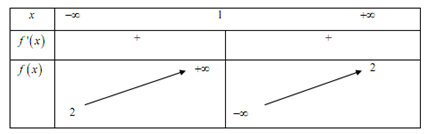
Cho cấp số cộng $\left( {{u_n}} \right)$ có ${u_2} = 2017$ và ${u_5} = 1945.$  Tính ${u_{2018}}$ .

Tính $\mathop {\lim }\limits_{x \to 2} \dfrac{{x - \sqrt {x + 2} }}{{\sqrt {4x + 1}  - 3}}$ bằng?

Chọn mệnh đề đúng:

Trong không gian với hệ tọa độ $Oxyz$, cho hai đường thẳng

$d:\left\{ \begin{array}{l}x = 1 + at\\y =  - 2 + t\\z =  - 2t\end{array} \right.$ và $d' :\dfrac{x}{2} = \dfrac{{y - 3}}{{ - 1}} = \dfrac{{z + 2}}{2}$.

      Với giá trị nào sau đây của $a$ thì $d$ và $d'$ song song với nhau?

Trong không gian với hệ tọa độ $Oxyz,$ cho điểm $A\left( {1;0;2} \right)$ và đường thẳng $d:\dfrac{{x - 1}}{1} = \dfrac{y}{1} = \dfrac{{z + 1}}{2}$. Viết phương trình đường thẳng $\Delta$ đi qua $A,$ vuông góc và cắt $d$.

Trong không gian với hệ tọa độ $Oxyz$ , phương trình nào dưới đây là phương trình mặt cầu tâm $I\left( { - 3;2; - 4} \right)$ và tiếp xúc với mặt phẳng $\left( {Oxz} \right)$?

 Mệnh đề nào sau đây là mệnh đề đúng ?

Điểm nào là ảnh của $M\left( {3; - 1} \right)$ qua phép đối xứng tâm $I\left( {1;2} \right)$ 

Cho hàm số $f\left( x \right) = A\sin \left( {\pi x} \right) + B{x^2}$ ($A, B$ là các hằng số) và $\int\limits_0^2 {f\left( x \right)dx = \dfrac{8}{3}.}$ Tính $B.$

Cho tứ diện $ABCD$ có $AB,AC,AD$ đôi một vuông góc. Chỉ ra mệnh đề sai trong các mệnh đề sau:

Gọi $S$ là tổng phần thực và phần ảo của số phức $w = {z^3} - i$, biết $z$ thỏa mãn $z + 2 - 4i = \left( {2 - i} \right)\overline {iz}$. Mệnh đề nào sau đây đúng?

Cho hình chóp tam giác đều $S.ABC$ có cạnh đáy bằng $a$ và mặt bên hợp với đáy một góc ${60^0}$. Thể tích khối chóp $S.ABC$ là:

Giá trị của $x$ thỏa mãn ${\log _{\frac{1}{2}}}(3 - x) = 2$ là

Trong các khẳng định sau, khẳng định nào sai?

Thể tích khối nón có bán kính đáy $r$, độ dài đường sinh $l$ là:

Cho biểu thức $S = C_{2017}^{1009} + C_{2017}^{1010} + C_{2017}^{1011} + C_{2017}^{1012}... + C_{2017}^{2017}$. Khẳng định nào sau đây đúng? 

Cho hàm số $y = \dfrac{{x - 2}}{{x + 2}}$ có đồ thị $(C)$. Tìm tọa độ giao điểm $I$ của hai đường tiệm cận của đồ thị $(C)$

Trong không gian $Oxyz$ cho mặt cầu $(S):{x^2} + {y^2} + {z^2} - 2x + 4y + 2z - 3 = 0$. Tính bán kính $R$ của mặt cầu $(S)$.

Trong không gian với hệ tọa độ $Oxyz$, cho $\overrightarrow {OM}  = 2\vec j - \vec k$ và $\overrightarrow {ON}  = 2\vec j - 3\vec i$. Tọa độ của $\overrightarrow {MN}$ là: 

Hàm số nào sau đây nghịch biến trên từng khoảng xác định?

Cho hàm số $y=f\left( x \right)$ có bảng biến thiên như sau:

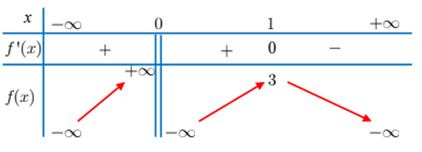
Với các giá trị thực của tham số $m$, phương trình $f\left( x \right)=m$ có nhiều nhất bao nhiêu nghiệm?

Tính $I = \int {\dfrac{{{{\cos }^3}x}}{{1 + \sin x}}dx}$ với $t = {\mathop{\rm sinx}\nolimits}$. Tính $I$ theo $t$?

Cho hàm số $y = f\left( x \right)$ xác định, liên tục trên $\mathbb{R}$ và có bảng biến thiên sau:

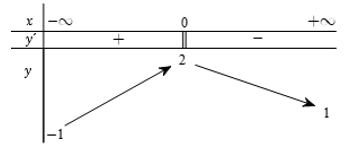
Khẳng định nào sau đây là đúng?

Tìm phần thực và phần ảo của số phức $z = 4 - 3i + {\left( {1 - i} \right)^3}$.

Trong không gian với hệ tọa độ $Oxyz$, cho mặt phẳng $\left( P \right):9x + 3y - 10z + 26 = 0$ và đường thẳng $d:\dfrac{{x + 1}}{2} = \dfrac{{y - 1}}{4} = \dfrac{{z - 2}}{3}$. Mệnh đề nào sau đây là đúng?

Cho hàm số $y = {x^3} - 3{x^2} - 9x + m$. Viết phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số.

Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như sau:

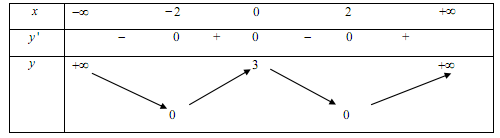
Khẳng định nào sau đây là khẳng định đúng?

Cho hàm số $y=\frac{1}{3}{{x}^{3}}-3{{x}^{2}}+x+1$ có đồ thị (C). Trong các tiếp tuyến với đồ thị (C), hãy tìm phương trình tiếp tuyến có hệ số góc nhỏ nhất.

Tìm TXĐ của hàm số $y = {\left( {{x^3} - 27} \right)^{\dfrac{\pi }{2}}}$ 

Trong các khẳng định dưới đây, khẳng định nào sai?

Tính tích phân $I=\int\limits_{1}^{2}{\ln \left( 1+x \right)\,\text{d}x}.$

Gieo một con xúc sắc cân đối và đồng chất $5$ lần liên tiếp. Tính xác suất để tổng số chấm ở hai lần gieo đầu bằng số chấm ở lần gieo thứ ba.

Diện tích hình phẳng giới hạn bởi nửa đường tròn ${x^2} + {y^2} = 2,y > 0$ và parabol $y = {x^2}$ bằng:

Thể tích khối tròn xoay thu được khi quay quanh trục $Ox$ hình phẳng giới hạn bởi đồ thị hàm số $y=\frac{\sqrt{3x+1}}{x+1},$ trục hoành và đường thẳng $x=1$ là

Gọi $F\left( x \right)$ là một nguyên hàm của hàm số $f\left( x \right) = \dfrac{{{x^2}\sin x + 2x\cos x}}{{x\sin x + \cos x}}.$ Biết $F\left( 0 \right) = 1,$ Tính giá trị biểu thức $F\left( {\dfrac{\pi }{2}} \right).$

Cho hình lăng trụ $ABC.A'B'C'$ có đáy $ABC$ là tam giác cân $AB = AC = a;\widehat {BAC} = {120^0}$ và $AB'$ vuông góc với $\left( {A'B'C'} \right)$ . Mặt phẳng $\left( {AA'C'} \right)$ tạo với mặt phẳng $\left( {A'B'C'} \right)$ một góc ${30^0}$. Thể tích khối lăng trụ $ABC.A'B'C'$ là:

Trong không gian với hệ tọa độ $Oxyz,$ cho các điểm $A\left( 0;1;2 \right),\,\,B\left( 2;-\,2;0 \right)$ và $C\left( -\,2;0;1 \right).$ Mặt phẳng $\left( P \right)$ đi qua $A,$ trực tâm $H$ của tam giác $ABC$ và vuông góc với mặt phẳng $\left( ABC \right)$ có phương trình là

Trong không gian với hệ tọa độ  $Oxyz$, cho các điểm  $A\left( {1,2, - 4} \right);{\rm{ }}B\left( {1, - 3,1} \right){\rm{ }} và {\rm{ }}C\left( {2,2,3} \right)$. Mặt cầu $(S)$ đi qua  $A,B,C$ và có tâm thuộc mặt phẳng $(xOy)$ có bán kính là :

Phương trình $\sin 2x + 3\sin 4x = 0$ có nghiệm là:

Cho hai hình vuông $ABCD,ABEF$ có chung cạnh $AB$ và nằm trong hai mặt phẳng khác nhau. Trên các đường chéo $AC$ và $BF$ ta lấy các điểm $M, N$ sao cho $AM = BN.$ Mặt phẳng $(P)$ chứa $MN$ và song song với $AB$ cắt $AD$ và $AF$ lần lượt tại $M’, N’.$ Khẳng định nào sau đây là đúng?

Cho hình chóp $S.ABCD$ có đáy là hình thang vuông tại $A$ và $B$, $AD = a,$ $AB = 2a,$ $BC = 3a,$ $SA = 2a$, $H$ là trung điểm cạnh $AB$, $SH$ là đường cao của hình chóp $S.ABCD$. Tính khoảng cách từ điểm $A$ đến mặt phẳng $\left( {SCD} \right)$.

Trong các mệnh đề sau, mệnh đề nào sai ?

Tính tích phân $I = \int\limits_{ - 5}^0 {\left| {{x^2} + 4x + 3} \right|dx}$ ta được kết quả là $I = \dfrac{a}{b}$ với $a,b$ nguyên dương và phân số $\dfrac{a}{b}$ tối giản. Khi đó $a - b$ có giá trị là:

Cho số phức $z$ thỏa mãn $\left| {z - 2} \right| = 2$. Biết rằng tập hợp các điểm biểu diễn các số phức $w = \left( {1 - i} \right)z + i$ là một đường tròn. Tính bán kính $r$ của đường tròn đó

Cho hình lăng trụ đều $ABC.A'B'C'$ có tất cả các cạnh bằng a. Gọi M là trung điểm của cạnh BC. Khoảng cách giữa hai đường thẳng AM và B’C là :

Đường thẳng qua $M\left( {1{\rm{ }};1} \right)$ và cắt elíp $\left( E \right){\rm{ }}:{\rm{ }}4{x^2} + {\rm{ }}9{y^2} = {\rm{ }}36$ tại hai điểm ${M_1},{\rm{ }}{M_2}$ sao cho $M{M_1} = {\rm{ }}M{M_2}$ có phương trình là

Trong không gian với hệ tọa độ $Oxyz$, cho mặt cầu $(S) : {\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 3} \right)^2} = 9$ và mặt phẳng  $(P) :2x - 2y + z + 3 = 0$. Gọi $M(a ; b ; c)$ là điểm trên mặt cầu $(S)$ sao cho khoảng cách từ $M$ đến mặt phẳng $(P)$ là lớn nhất. Khi đó:

Cho hình chóp $S.ABC$ có $SA \bot (ABC);AC = b,AB = c,\widehat {BAC} = \alpha$. Gọi $B',C'$ lần lượt là hình chiếu vuông góc của $A$ lên $SB,SC$. Tính bán kính mặt cầu ngoại tiếp khối chóp $A.{\rm{ }}BCC'B'$ theo $b,c,\alpha$

Cho hàm số $y = \dfrac{{x + 2}}{{x - 1}}$ có đồ thị $\left( C \right)$. Gọi $d$ là khoảng cách từ điểm $A\left( {1;1} \right)$ đến một tiếp tuyến bất kỳ của đồ thị $\left( C \right)$. Tìm giá trị lớn nhất của $d$?