Cho hàm số \(y = \dfrac{{x + 2}}{{x - 1}}\) có đồ thị \(\left( C \right)\). Gọi $d$ là khoảng cách từ điểm \(A\left( {1;1} \right)\) đến một tiếp tuyến bất kỳ của đồ thị \(\left( C \right)\). Tìm giá trị lớn nhất của $d$?
Trả lời bởi giáo viên
Ta có \(y' = \dfrac{{ - 3}}{{{{\left( {x - 1} \right)}^2}}}\)
\( \Rightarrow \) Phương trình tiếp tuyến của đồ thị hàm số tại điểm \(M\left( {{x_0};{y_0}} \right)\) là:
$\begin{array}{l}y = \dfrac{{ - 3}}{{{{\left( {{x_0} - 1} \right)}^2}}}\left( {x - {x_0}} \right) + 1 + \dfrac{3}{{{x_0} - 1}} \\ \Leftrightarrow \dfrac{{ - 3}}{{{{\left( {{x_0} - 1} \right)}^2}}}x - y + \dfrac{{3{x_0}}}{{{{\left( {{x_0} - 1} \right)}^2}}} + 1 + \dfrac{3}{{{x_0} - 1}} = 0\left( \Delta \right)\\ \Rightarrow d\left( {A;\Delta } \right) = \dfrac{{\left| {\dfrac{{ - 3}}{{{{\left( {{x_0} - 1} \right)}^2}}} - 1 + \dfrac{{3{x_0}}}{{{{\left( {{x_0} - 1} \right)}^2}}} + 1 + \dfrac{3}{{{x_0} - 1}}} \right|}}{{\sqrt {\dfrac{9}{{{{\left( {{x_0} - 1} \right)}^4}}} + 1} }} \\= \dfrac{{\left| {\dfrac{{ - 3 + 3{x_0} + 3{x_0} - 3}}{{{{\left( {{x_0} - 1} \right)}^2}}}} \right|}}{{\sqrt {\dfrac{9}{{{{\left( {{x_0} - 1} \right)}^4}}} + 1} }}\\ = \dfrac{{\dfrac{{\left| {6{x_0} - 6} \right|}}{{{{\left( {{x_0} - 1} \right)}^2}}}}}{{\dfrac{{\sqrt {{{\left( {{x_0} - 1} \right)}^4} + 9} }}{{{{\left( {{x_0} - 1} \right)}^2}}}}} \\= \dfrac{{6\left| {{x_0} - 1} \right|}}{{\sqrt {{{\left( {{x_0} - 1} \right)}^4} + 9} }} \\= 6\sqrt {\dfrac{{{{\left( {{x_0} - 1} \right)}^2}}}{{{{\left( {{x_0} - 1} \right)}^4} + 9}}} \end{array}$
Đặt \(t = {\left( {{x_0} - 1} \right)^2}\,\,\left( {t \ge 0} \right) \Rightarrow d = 6\sqrt {\dfrac{t}{{{t^2} + 9}}} \)
Mà
$\begin{array}{l}
{t^2} + 9 \ge 2\sqrt {{t^2}.9} = 6t \Rightarrow \frac{t}{{{t^2} + 9}} \le \frac{t}{{6t}} = \frac{1}{6}\\
\Rightarrow 6.\sqrt {\frac{t}{{{t^2} + 9}}} \le 6.\sqrt {\frac{1}{6}} = \sqrt 6 \\
\Rightarrow {d_{\max }} = \sqrt 6
\end{array}$
Dấu "=" xảy ra khi t=3
$ \Leftrightarrow {\left( {{x_0} - 1} \right)^2} = 3 \Leftrightarrow \left[ \begin{array}{l}
{x_0} - 1 = \sqrt 3 \\
{x_0} - 1 = - \sqrt 3
\end{array} \right. $ $\Leftrightarrow \left[ \begin{array}{l}
{x_0} = \sqrt 3 + 1\\
{x_0} = - \sqrt 3 + 1
\end{array} \right.$
Hướng dẫn giải:
Viết phương trình tiếp tuyến $\left( d \right)$ của đồ thị hàm số tại điểm \(M\left( {{x_0};{y_0}} \right)\).
Tính khoảng cách từ điểm $A$ đến $d$.
Tìm GTLN của khoảng cách $d$.
Giải thích thêm:
Đối với HS lớp 12 có thể tìm GTLN của d như sau:
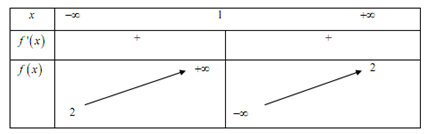
Xét hàm số \(f\left( t \right) = \dfrac{t}{{{t^2} + 9}}\,\,\,\left( {t > 0} \right)\)
Có \(f'\left( t \right) = \dfrac{{{t^2} + 9 - t.2t}}{{{{\left( {{t^2} + 9} \right)}^2}}} = \dfrac{{ - {t^2} + 9}}{{{{\left( {{t^2} + 9} \right)}^2}}} = 0 \Leftrightarrow t = 3\)
\(f\left( 3 \right) = \dfrac{3}{{18}} = \dfrac{1}{6} \Rightarrow d = \sqrt 6 \Rightarrow {d_{max}} = \sqrt 6 \)